Сила давления на цилиндрическую поверхность

Рассмотрим некоторую ограниченную часть твердой цилиндрической поверхности, которую назовем цилиндрической стенкой.

Пусть рассматриваемая стенка находится под односторонним воздействием покоящейся жидкости. Разобьем стенку на элементарные площадки. В силу малости площадок будем считать их плоскими.

dP = ρdω.

Для цилиндрической стенки кругового сечения элементарные силы давления будучи нормальными к элементарным площадкам направлены по радиусам и следовательно пересекаются в центре сферы или круга.

Расчетная схема А.

z

x ω_z

y

h^` _ц.т. W_A

P

ω_x

_C

_D P_x

Ө

P₂ P

Рассмотри силу избыточного давления на цилиндрическую стенку, при этом ось Оy направим параллельно образующей, а ось Оz вертикально вверх. Значение силы давления на цилиндрическую поверхность определяется:

P = , где P_x и P_y – горизонтальная и вертикальная составляющая силы давления.

Выделим на цилиндрической поверхности элементарную площадку, элементарная сила которой равна ρg h dω.

dP = ρg h dω.

Найдем горизонтальную dP_x и вертикальную dP_z составляющие силы dP.

dP_x = dPcos(dP,Ox) = ρg h dω cos(dP,Ox);

dP_z = dPcos(dP,Oz) = ρg h dω cos(dP,Oz)/

Учитывая, что

dω cos(dP,Ox) = dω_x;

dω cos(dP,Oz) = dω_z;.

Имеем, dP_x = ρg h dω_x (*)

dP_z = ρg h dω_z

dω_x – проекция элементарной площадки на плоскость перпендикулярную оси Оx

dω_z – проекция элементарной площадки на плоскость перпендикулярную оси Оz

Проинтегрировав (*) получим для горизонтальной составляющей силы Р: Р_х = ρg h_ц.т. ω_x

ω_x – проекция всей цилиндрической поверхности на плоскость нормальную к оси Ох;

h_ц.т – глубина центра тяжести проекции ω_x под пьезометрической плоскостью.

Для вертикальной составляющей: Р_z = ρg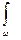zdω_z

Координата центра давления равна:

l_ц.д. = h_ц.д. = h_ц.т. + J₀/ω h_ц.т

P_z = ρg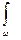zdω_{z =} ρg W_D, где W_D = 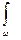zdω_z.

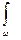zdω_z – представляет собой объем призмы, ограниченной снизу цилиндрической поверхностью, а сверху ее проекцией на пьезометрическую плоскость.

Все направляющие этой призмы вертикальные и прямые. Полученное таким образом тело называется телом давления. Тело давления может быть положительным и отрицательным.

Дата добавления: 2014-01-05