
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вращение вокруг линий уровня
|
|
|
|
Вращение вокруг линий уровня применяют в тех случаях, когда данную плоскую фигуру требуется совместить с какой-либо плоскостью, параллельной плоскости проекций. В таком положении плоская фигура проецируется на соответствующую плоскость проекций без искажения.
На рис. 10.12 показано вращение некоторой точки А вокруг горизонтальной оси h || П1. В этом случае плоскостью вращения точки А (плоскость, в которой расположена траектория движения точки А – окружность) будет являться плоскость Σ, перпендикулярная оси вращения (Σ ^ h) и, следовательно, горизонтальной плоскости проекций Σ ^ П1.
Точка А будет перемещаться по окружности с центром в точке С (точка пересечения оси вращения с плоскостью Σ). С = h ∩ Σ. Радиус этой окружности равен расстоянию от точки А до оси вращения h (R=АС).
Плоскость Σ – горизонтально проецирующая (Σ ^ П1), поэтому траектория движения точки А в пространстве (окружность) спроецируется на плоскость П1 в прямую, совпадающую с горизонтальным следом плоскости Σ (ΣП1).
Когда точка А, вращаясь вокруг оси h, совместится с плоскостью, параллельной плоскости проекций П1, радиус вращения этой точки R=CA займет горизонтальное положение и спроецируется на П1 без искажения: C1A1 = CA=R.
План решения задачи следующий:
1. Через горизонтальную проекцию А1 точки А проведем горизонтальный след плоскости Σ (Σ1 ^ h1) и отмечаем центр вращения С (С1С2).
2. Определяем натуральную величину радиуса вращения Rвр.=А0С1 (как гипотенузу прямоугольного треугольника, катетами которого являются горизонтальная проекция радиуса вращения А1С1 и разность координат Z точек А и С, ∆ Z=ZА–ZC). Гипотенуза треугольника ∆ С1А1А0, С1А0=Rвр..
Новое, после поворота, положение точки А1/ находится в месте пересечения дуги окружности, проведенной из горизонтальной проекции центра вращения С1 радиусом, равным С1А0 с горизонтальным следом Σ1 плоскости Σ.

Рис. 10.12
На рис. 10.13 показан пример вращения треугольника АВС вокруг его горизонтали АD (AD Ì ABC, AD || П1). Точки D и А не меняют своего положения в процессе вращения треугольника (А1 º А1 /, D1 º D1 /), т.к. они принадлежат оси вращения h (D Î h, А Î h), а горизонтальные проекции точек В и С перемещаются по прямым, перпендикулярным h1 (B1B1 /^ h1 и С1С1 /^ h1). Положение точки В1/ после поворота треугольника определено описанным выше способом (О1В1/=О1В0=Rвр.). В результате вращения треугольник АВС занял положение А1/ B1/C1/, параллельное плоскости П1, и спроецировался на эту плоскость без искажений: ç А1/В1/C1 / ç= ç ABC ç. Фронтальная проекция треугольника после поворота А2/B2/C2/ - прямая линия, параллельная оси координат.
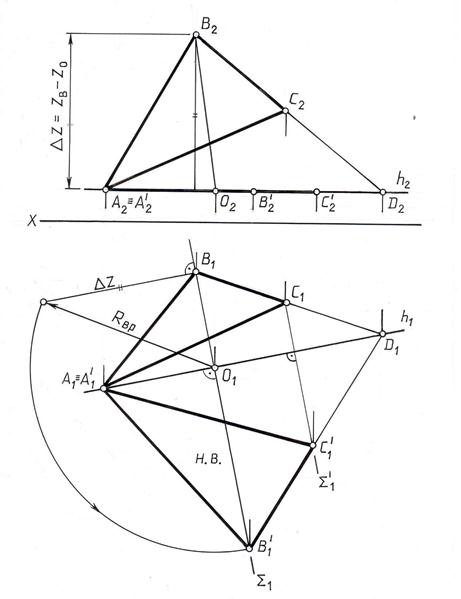
Рис. 10.13
Лекция 11.
Плоскости, касательные к поверхностям
Общие понятия. Способы построения касательных плоскостей.
Основные типы задач по построению касательных.
Плоскостью, касательной к криволинейной поверхности в обыкновенной точке А, называется плоскость, определяемая двумя пересекающимися прямыми, касательными к этой поверхности в точке А (рис. 11.1).
Обыкновенными точками поверхности являются точки, в которых можно построить только одну касательную плоскость к поверхности. Особыми точками поверхности считаются те, в которых нельзя построить только одну касательную плоскость. Примерами особых точек поверхности являются: вершина конуса, точка ребра возврата и т.д., касательная плоскость в которых может быть однозначно не определена, т.е. может быть проведено множество плоскостей.
Касательные плоскости применяются при построении линий пересечения поверхностей, при построении очерков поверхностей, при построении собственных теней поверхности, при построении нормали к поверхности и т.д.
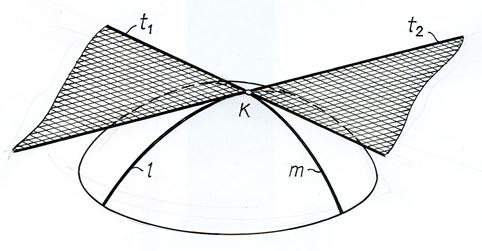
Рис. 11.1
Для того, чтобы провести прямую, касательную к поверхности в определенной ее точке, достаточно через эту точку провести на поверхности любую кривую и построить касательную прямую к ней. Поскольку через одну точку поверхности можно провести множество кривых линий, то в одной точке поверхности можно провести и множество касательных прямых.
Все эти касательные будут лежать в одной плоскости, являющейся касательной плоскостью к поверхности.
Таким образом, касательная плоскость к поверхности – это геометрическое место прямых, касающихся данной поверхности в обыкновенной точке.
Чтобы задать касательную плоскость, достаточно построить две касательные прямые к поверхности.
Касательной к поверхности называется прямая, являющаяся касательной к какой-либо линии, принадлежащей этой поверхности.
В качестве линий поверхности обычно используются линии ее определителя или линии, которые могут быть легко построены графически. Например, у поверхностей вращения это параллели и меридианы, у линейчатой поверхности – ее прямолинейные образующие.
Касательная плоскость может иметь с поверхностью только одну общую точку. В этом случае все линии поверхности, пересекающиеся в рассматриваемой точке, находятся по одну сторону от касательной плоскости. Такие точки поверхности называются эллиптическими. Поверхности, у которых все точки эллиптические, являются выпуклыми криволинейными поверхностями. К ним относятся сфера, эллипсоид вращения, параболоид вращения, закрытый тор и т. д.
Касательная плоскость может иметь с поверхностью общую линию (прямую или кривую). Например, касательная плоскость касается торсовых поверхностей вдоль их образующей – прямой линии. Она является касательной плоскостью для всех его точек, лежащих на этой прямой. Точки поверхности, удовлетворяющие этому условию, называются параболическими. К ним относятся точки развертываемых прямолинейных поверхностей – конических, цилиндрических и с ребром возврата.
Касательная плоскость к поверхности в данной точке может пересекать поверхность, к которой она проведена. В пересечении могут получаться пересекающиеся две прямые, две кривые, либо прямая и кривая линии.
Точки поверхности, касательная плоскость в которых пересекает поверхность, называются гиперболическими. Такие точки касания находятся на внутренней поверхности открытого тора.
Возможны следующие основные случаи построения касательных плоскостей к поверхностям:
1. через точку на самой поверхности
2. через точку, лежащую вне поверхности
3. параллельно заданной прямой
4. параллельно заданной плоскости
5. через прямую, лежащую вне поверхности
Построение касательной плоскости может выполняться несколькими способами:
1) построением двух касательных прямых к двум кривым линиям поверхности (обычно для эллиптических точек касания)
2) построением касательного следа плоскости к одноименному следу поверхности
3) построением вспомогательных сечений поверхности с последующим проведением к ним касательных прямых определенного направления
Последние два способа применяются обычно для гиперболических и параболических точек касания.
Рассмотрим примеры решения задач различных случаев.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1657; Нарушение авторских прав?; Мы поможем в написании вашей работы!