Тип 1 . Построить касательную плоскость к поверхности через точку на ней

Задача 1. Построить плоскость, касательную к поверхности сферы в точке К (рис. 11.2).

Выберем две кривые линии, проходящие через точку К. Целесообразно взять наиболее графически простые линии – окружности (параллели и меридианы) – n и m.

К этим двум окружностям в точке К проводим касательные, причем каждую в плоскости своей окружности, т.е. t лежит в вертикальной, а t^′ – в горизонтальной плоскостях.

Построенные касательные t и t^′ и задают искомую касательную плоскость.

В рассматриваемой задаче точка К - эллиптическая точка касания. ОК - радиус, являющийся нормалью к касательной плоскости в точке К. Построенная плоскость ему перпендикулярна.

Рис. 11.2

Задача 2. Построить касательную плоскость к поверхности вращения

в точке К (рис. 11.3).

В качестве линий, задающих касательную плоскость, примем две

прямые, одна из которых является касательной к окружности - параллели, проходящей через точку К, вторая – касательной к меридиану, проходящему через эту же точку.

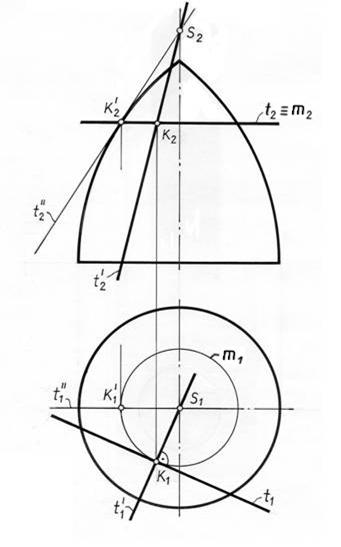
Рис. 11.3

Для того, чтобы провести касательную к меридиану, повернем его до

совмещения с главным меридианом и проведем касательную t^′′ ₂ в точке

К′₂, лежащей на той же окружности параллели, что и точка К, до пересечения с осью симметрии фигуры в точке S. Через эту же точку S пройдет касательная t^′ ₂ после возвращения поворачиваемого меридиана в исходное состояние. Для ее построения соединяем S₂ и К₂.

Вторая касательная t строится таким образом. Ее фронтальная проекция t ₂ на фронтальной плоскости проекций совпадает с проекцией окружности параллели m. Горизонтальная проекция t ₁ строится как касательная прямая к горизонтальной проекции окружности – параллели m₁.

Касательные t^′ и t^′ и определят искомую касательную плоскость.

Отметим, что в этой задаче точка касания К также представляет собой эллиптическую точку касания.

Задача 3. Построить касательную к цилиндру в точке К (рис. 11.4).

Рис. 11.4

Элементом касания плоскости к цилиндру будет являться образующая цилиндра t, на которой лежит точка К. В этой задаче точка касания К является одной из геометрического множества параболических точек касания, лежащих на одной образующей цилиндра. С этой образующей совпадает первая касательная прямая t к этой поверхности.

Вторая касательная прямая пройдет через точку N, лежащую в основании цилиндра. Эта точка является точкой пересечения образующей t с плоскостью основания цилиндра.

Построенные касательные прямые t и t ′ и образуют касательную плоскость к цилиндру в точке К.

Дата добавления: 2014-01-05