Теорема 2.1

Любое отношение эквивалентности определяет разбиение множества на попарно непересекающиеся подмножества, т.е. на классы.

Доказательство:

Рассмотрим любое произвольное множество 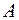. Перед доказательством теоремы вспомним, что означает разбить множество 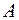на классы. В соответствии с операцией разбиения это означает найти такие множества , называемые классами, для которых справедливо следующее:

- объединение всех классов , составит множество : ;

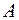- пересечение всех классов пусто:, .

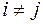Если на множестве 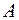задать отношение эквивалентности , то всевозможные сечения (или окрестности единичного радиуса) образуют классы. Докажем это. Сначала докажем, что объединение всех сечений даст множество 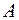. Запишем высказывательную форму отношения: 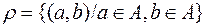. Возьмём любой произвольный элемент 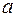из множества 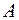: 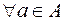. Рассмотрим сечение отношения 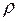элементом :

.

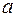Образуем такие сечения для всех элементов 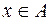. Так как 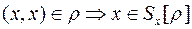. Следовательно, каждый элемент множества 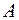будет принадлежать какому-либо сечению. Тогда можно сделать вывод, что 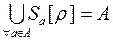. Докажем, что пересечение всех классов является пустым множеством. Доказательство будем проводить методом от противного. Допустим, что сечения отношения эквивалентности 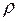по некоторым элементам и пересекаются, т.е. . Тогда в пересечении этих множеств присутствует хотя бы один элемент 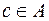: 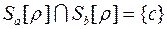. Очевидно, что 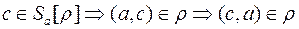; и . В сечении 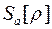рассмотрим некоторый элемент . Тогда можно записать . Рассмотрим следующие элементы множества 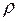: 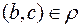, 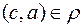и . Тогда справедливо соотношение: 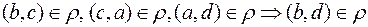. Следовательно .

Таким образом, отношение эквивалентности находится во взаимосвязи с разбиением множества.

Подмножество элементов, эквивалентных некоторому элементу 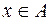, называется классом эквивалентности.

Все элементы одного класса эквивалентны между собой и каждый элемент может находиться только в одном классе. Значит, каждому отношению эквивалентности на множестве 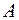соответствует некоторое разбиение множества на классы. Необходимым и достаточным условием для того, чтобы некоторое отношение 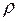позволяло разбить множество на классы является совокупность свойств рефлексивности, симметричности и транзитивности.

Дата добавления: 2014-01-05