Декартово произведение

Определение. Декартовым произведением двух отношений R₁ (R₁₁, R_12, …,R_1n), R₂,(R₂₁, R_22, …,R_2m) называется отношение, заголовок которого является сцеплением заголовков отноше­ний R₁ и R₂:

(R₁₁, R_12, …,R_1n,R₂₁, R_22, …,R_2m),

а тело состоит из кортежей, являющихся сцеплением корте­жей отношений R₁ и R₂:

(r₁₁, r_12, …,r_1n,r₂₁, r_22, …,r_2m),

таких, что:

(r₁₁, r_12, …,r_1n)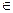R₁, (r₂₁, r_22, …,r_2m) 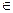R₂,

При выполнении прямого произведения двух отношений по­лучается отношение, кортежи которого являются конкатена­цией (сцеплением) кортежей первого и второго операндов. Синтаксис операции декартового произведения:

R₁ times R₂

Замечание. Мощность произведения R₁ times R₂ равна произведению мощностей отношений R₁ и R₂, т. к. каждый кортеж отношения R₁ соединяется с каждым кортежем отношения R_2.

Если в отношениях R₁ и R₂ имеются атрибуты с одинаковыми наименованиями, то перед выполнением операции декартового произведения такие атрибуты необходимо переименовать. При перемножении отношений совместимость по типу не требуется.

Пример. Пусть даны два отношения R₁ и R₂ с информацией о студентах и дисциплинах (рис. 6.5). Декартово произведение отношений R₁ и R₂ будет иметь вид, представленный на рис. 6.6.

Отношение R₁ (Студенты)

Личный номер	Фамилия
	Котова
	Серов
	Леонидов

Отношение R₂ (Название дисциплины)

Код дисциплины	Название дисциплины
	Высшая математика
	История
	Иностранный язык

Рис. 6.5. Примеры отношений R₁ и R₂

Отношение R₁ times R₂

Личный номер	Фамилия	Код дисциплины	Название дисциплины
	Котова		Высшая математика
	Котова		История
	Котова		Иностранный язык
	Серов		Высшая математика
	Серов		История
	Серов		Иностранный язык
	Леонидов		Высшая математика
	Леонидов		История
	Леонидов		Иностранный язык

Рис. 6.6. Результат операции декартова произведения для отношений R₁ и R₂

Замечание. Операция декартова произведения непосредственно для реальных запросов не используется, но она важна для выполнения специальных операций [20, С. 55-64].

Дата добавления: 2014-01-05