Основные операции с нечеткими множествами

Нечеткая логика создавалась Л. Заде [11] как расширение классической формальной логики с целью реализации моделирования явлений реального мира, которые не всегда укладываются в рамки классической логики. В основе такого расширения лежит аксиома, по которой операции формальной логики должны являться частным случаем операций нечеткой логики. На этом принципе происходит построение теоретико-множественных операций и отношений.

Дополнение 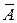нечеткого множества А определяется в соответствии с определением (9.1), где функция принадлежности = 1 - 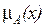. Таким образом, закон двойного отрицания для данных нечетких логик выполняется.

Пересечение нечетких множеств А и В определяется как нечеткое множество вида:

А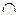В = {():}, (9.7)

где результат операции зависит от способа задания степени принадлежности

. Наиболее распространены следующие способы [10]:

= min (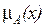;), , (Л. Заде, 1965); (9.8)

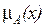
= , , (B.M. Pfeiffer 1996). (9.9)

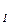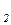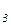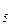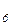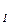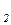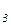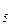Пример. Дана предметная область Х={х; х;х;х;х;х}, на котором определены нечеткие множества А={1/ х:0,8/ х;0,6/ х;0,4/ х;0,2/ х;0/ х}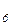

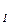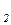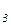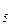и В={0/ х:0,2/ х;0,4/ х;0,6/ х;0,8/ х;1/ х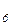}, где принята запись a/x ~ (a;x).

Определим А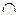В, используя (9.8),(9.9).

Согласно (9.7),(9.8) имеем:

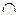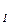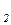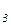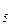АВ={0/ х:0,2/ х;0,4/ х;0,4 / х;0,2/ х;0/ х}.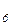

Согласно (9.7),(9.9) имеем:

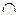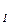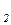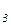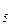АВ={0/ х:0,16/ х;0,24/ х;0,24 / х;0,16/ х;0/ х}.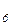

Как видим, результат вычисления А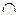В оказывается различным в зависимости от принятого способа определения , опирающегося на субъективные соображения. В частности, способ (9.8) рекомендуют использовать для систем, в которых метод обработки информации близок к логическому, когда большинство зависимостей между входными и выходными параметрами системы носят детерминированный характер, т.е. значения функций принадлежностей параметров системы достаточно близки к 1. Преимуществом способа (9.9) является то, что значение зависит от значений обеих функций принадлежност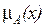и и . Поэтому потери информации здесь не так существенны, как в способе (9.8).

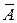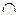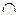
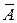
Из условия рассмотренного примера, согласно определения дополнения, видно, что В=. Но, как следует из разобранного примера, в обоих случаях АВ= А. Это означает, в нечеткой логике закон противоречия выполняется не всегда. В то же время, как легко убедиться, идемпотентность, коммутативность и ассоциативность пересечения нечетких множеств выполняются.

Объединение нечетких множеств А и В определяется как нечеткое множество вида:

АВ = {():}, (9.10)

где результат операции зависит от способа задания степени принадлежности

. Наиболее распространены следующие способы [10;11]:

= mах (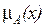;), ; (9.11)

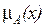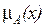
= +-, . (9.12)

Пример. Определим АВ, используя (9.11),(9.12) и данные предыдущего примера.

Согласно (9.10),(9.11) имеем:

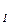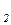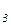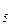АВ={1/ х:0,8/ х;0,6/ х;0,6 / х;0,8/ х;1/ х}.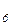

Согласно (9.10),(9.12) имеем:

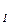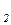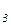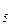АВ={1/ х:0,84/ х;0,76/ х;0,76 / х;0,84/ х;1/ х}.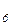

Наличие различных результатов при вычислении АВ и рекомендации по практическому применению способов (9.11), (9.12) объясняются теми же соображениями, что и при вычислении А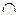В. Отметим, что для данной предметной области Х универсальное множество имеет вид:

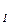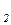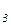U = {1/ х:1/ х;1/ х;1/ х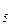;1/ х;1/ х}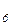

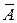
и, таким образом, данные рассматриваемого примера показывают, что АВ= АU, т.е. в нечеткой логике закон исключенного третьего, вообще говоря, выполняется не всегда. В то же время легко убедиться, что идемпотентность, коммутативность и ассоциативность объединения нечетких множеств имеют место.

Дата добавления: 2014-01-05