
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейные однородные уравнения с постоянными коэффициентами
|
|
|
|
Линейное однородное уравнение 2-ого порядка
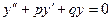 (1)
(1)
p, q — постоянные действительные числа
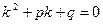 (2) характеристическое уравнение, его корни
(2) характеристическое уравнение, его корни
 ,
, 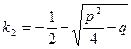
При этом возможны следующие случаи:
1. 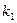 и
и 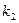 — действительные и притом не равные между собой числа (
— действительные и притом не равные между собой числа (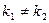 ). Тогда общее решение имеет вид
). Тогда общее решение имеет вид  (3)
(3)
2. 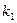 и
и 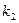 — комплексные числа
— комплексные числа
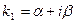 ,
, 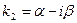 , где
, где  ,
, 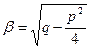
Общее решение имеет вид  (4)
(4)
3. 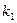 и
и 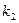 — действительные равные числа (
— действительные равные числа ( ).
).
Общее решение имеет вид  (5)
(5)
Пример 9.1. Решить уравнение
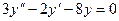
Решение. Характеристическое уравнение

 ;
; 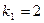 ,
, 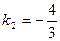
Общее решение 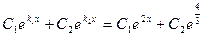
Пример 9.2. Решить уравнение
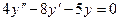
Решение

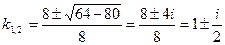 ;
; 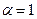 ,
, 
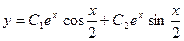
10. Неоднородные линейные уравнения 2-ого порядка с постоянными коэффициентами.
Это уравнение вида
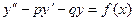 (1)
(1)
Сводная таблица видов частных решений для различных видов правых частей.
| № | Правая часть дифференциальных уравнений | Корни характеристического уравнения | Виды частного решения |
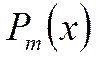 
| 1. Число 0 не является корнем характеристического уравнения. | 
| |
| 2. Число 0 — корень характеристического уравнения кратного S. | 
| ||

| 1. Число 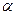 не является корнем характерного уравнения. не является корнем характерного уравнения.
| 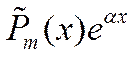
| |
2. Число 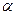 является корнем характерного уравнения кратности S. является корнем характерного уравнения кратности S.
| 
| ||
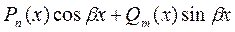
| 1. Число 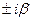 не является корнем характерного уравнения. не является корнем характерного уравнения.
|
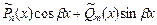
| |
2. Число 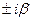 является корнем характерного уравнения кратности S. является корнем характерного уравнения кратности S.
|
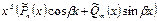
| ||

| 1. Число  не является корнем характерного уравнения. не является корнем характерного уравнения.
|
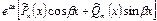
| |
2. Число  является корнем характерного уравнения кратности S. является корнем характерного уравнения кратности S.
|
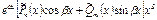
|
Пример 10.1. Решить уравнение
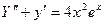
Решение. Характеристическое уравнение
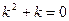
 ,
, 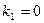 ,
, 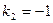
Общее решение однородных уравнений имеет вид: 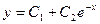
Правая часть уравнения 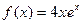 ,
, 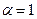 т.к.
т.к. 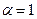 не является корнем характеристического уравнения, то частное решение неоднородного уравнения имеет вид (см. табл. Случай 2/1)
не является корнем характеристического уравнения, то частное решение неоднородного уравнения имеет вид (см. табл. Случай 2/1)
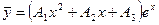
Подставляя его в исходное уравнение и сокращая обе части уравнения на 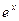 , будем иметь
, будем иметь
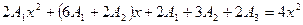
Приравнивая коэффициенты при одинаковых степенях в левой и правой частях равенства, получаем линейную систему уравнений для нахождения коэффициентов 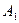 ,
,  и
и  :
:

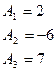

Общее решение данного уравнения 
Пример 10.2. Найти общее решение уравнения
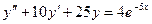
Решение: характеристическое уравнение k2+ 10k + 25=0 имеет двукратный корень k1 = k2=-5, поэтому y= (C1 +C2 x) e-5x.
Т. к. к=-5 является корнем характеристического уравнения кратности s=2, то частное решение неоднородного уравнения ищем в виде (см. табл., случай 2(2)):


Подставляя выражения для y,y!,y”в исходное уравнение, получаем
2Ae-5x =4e-5x, A=2, y = 2x2e-5x. Общее решение данного уравнения

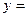
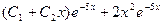
Пример 10.3 Найти частное решение уравнения

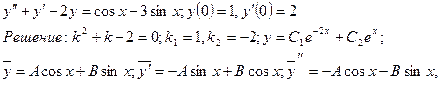
Подставляя выражения для y,y!,y”в исходное уравнение, получаем:
(B-3A) cosx +(-3B-A) sinx = cosx –3 sinx,

Найдем С1 и С2, используя начальные условия:
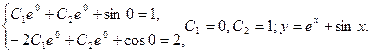
Пример 10.4. Решить уравнение:
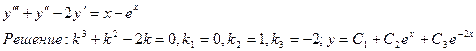
т. к. 0- простой корень характеристического уравнения, т.е.s=1, то частное решение ищем в виде:

Геометрические и физические задачи.
1. Чтобы решить геометрические задачи, надо построить чертеж, обозначить искомую кривую через 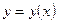 (если задача решается в прямоугольных координатах) и выразить все упоминаемые в задаче величины через
(если задача решается в прямоугольных координатах) и выразить все упоминаемые в задаче величины через 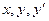 . Тогда данное в условии задачи соотношение превращается в дифференциальное уравнение, из которого можно найти искомую функцию
. Тогда данное в условии задачи соотношение превращается в дифференциальное уравнение, из которого можно найти искомую функцию 
2. В физических задачах надо прежде всего решить, какую из величин взять за независимое переменное, а какую – за искомую функцию. Затем надо выразить, на сколько изменится искомая функция y, когда независимое переменное x получит приращение  , т.е. выразить разность
, т.е. выразить разность 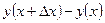 через величины, о которых говорится в задаче. Разделив эту разность на
через величины, о которых говорится в задаче. Разделив эту разность на  и перейдя к пределу при
и перейдя к пределу при  ®0,получим дифференциальное уравнение, из которого можно найти искомуу функцию.
®0,получим дифференциальное уравнение, из которого можно найти искомуу функцию.
1. Найти кривые, сумма длин нормали и поднормали есть величина постоянная, равная а.
Решение: Длина поднормали равна |y y¢|, а длина нормали |y  |. Т.о, уравнение, которому должны удовлетворять искомые кривые, имеет вид:
|. Т.о, уравнение, которому должны удовлетворять искомые кривые, имеет вид:
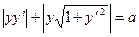
Разрешая его относительно y¢, находим (учитывая оба возможных знака):
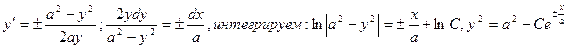
Условию задачи отвечают только С>0: из уравнения семейства кривых находим:
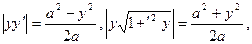 поэтому, чтобы выполнялось условие
поэтому, чтобы выполнялось условие 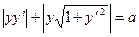 , нужно, чтобы |a2 – y2 |= a2 – y 2, т.е. y 2 < a2, отсюда и следует, что С >0.
, нужно, чтобы |a2 – y2 |= a2 – y 2, т.е. y 2 < a2, отсюда и следует, что С >0.
2. В комнате, где температура 20 0 С, некоторое тело остыло за 20мин. от 100 0 С до 60 0 С. Найти закон охлаждения тела, через сколько минут оно остынет до 300 С? Повышением температуры в комнате пренебречь.
Решение: В силу закона Ньютона (скорость охлаждения пропорциональна разности температур) можем написать:
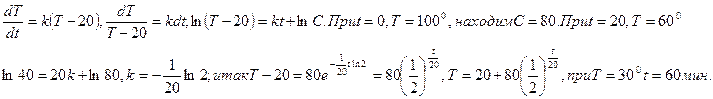 3. Найти уравнение кривой, проходящей через точку А(0,1), если известно, что в каждой точке нормаль к кривой отсекает на оси абсцисс отрезок, равный квадрату радиуса-вектора этой точки.
3. Найти уравнение кривой, проходящей через точку А(0,1), если известно, что в каждой точке нормаль к кривой отсекает на оси абсцисс отрезок, равный квадрату радиуса-вектора этой точки.

y
 |
M (x,y)
1 A
 0 B x
0 B x
Пусть точка М(х, у) – произвольная точка искомой кривой, МВ- нормаль к кривой в т.М, а В – точка пересечения нормали с осью абсцисс. Уравнение нормали к кривой в т.М имеет вид:
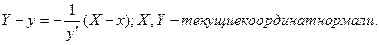
Найдем абсциссу т.В. Полагая в уравнении нормали 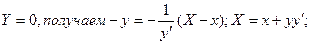 Квадрат радиуса- вектора т.М равен x2 +y2. По условию задачи
Квадрат радиуса- вектора т.М равен x2 +y2. По условию задачи
 это уравнение Бернулли при a=-1. Подстановкой
это уравнение Бернулли при a=-1. Подстановкой

Воспользовавшись начальным условием (кривая проходит черех точку А(0,1)), найдем значение произвольной постоянной С=1. Т.о., уравнение 
является уравнением искомой кривой.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Решить уравнения:
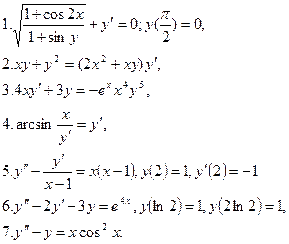
8. За 30 дней распалось 50 % первоначального количества радиоактивного вещества. Через сколько времени останется 1 % от первоначального количества?
(Закон радиоактивного распада: количество радиоактивного вещества, распадающегося за единицу времени, пропорционально количеству этого вещества, имеющегося в рассматриваемый момент).
9. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы касания.
Ответы:
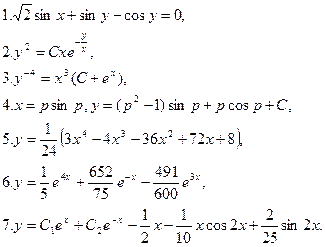
8.»200 дней.
9.y=Cx2.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
1. Н.С. Пискунов. Дифференциальное и интегральное исчисление. Т 2, М.: Наука, 1985.
2. Сборник задач по математике для вузов под ред. А.В. Ефимова, Б.П. Демидовича, часть 2,М.: Наука, 1981.
3. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Т 2, 3,М.: Наука, 1970.
4. Г.Н Берман. Сборник задач по курсу математического анализа. М.:Наука, 1976.
5. А.Ф.Филиппов. Сборник задач по дифференциальным уравнениям. М.:Наука, 1973.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 909; Нарушение авторских прав?; Мы поможем в написании вашей работы!