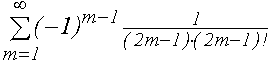Элементарные математические функции

Из многообразия т.н. элементарных встроенных математических функций отметим лишь некоторые наиболее известные или оригинальные. Аргументами большинства из приведенных ниже функций являются не только скаляры, но и массивы.

pi = 4*atan(1)=imag(log(-1))=3.1415926535897..;

abs(X) - абсолютная величина: для комплексного числа a+bi его модуль равен 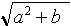/ abs(3-4i)=5, abs(-13)=13;

angle(X) - аргумент комплексного числа (из диапазона [-p,p ]): комплексное X=a+bi представимо как r·e^{i j}, где a = r cos j, b = r sin j:

>> angle(3+4i)	ans = 0.9273;	>> angle(1)	ans = 0;
>> angle(4+3i)	ans = 0.6435;

real(X), imag(X) - действительная и мнимая часть числа;

conj(X) - комплексно-сопряженное:

>>conj(2+3i)

ans = 2.0000 - 3.0000i;

ceil(X), fix(X), floor(X), round(X) - округления (до ближайшего целого, не меньшего Х; отбрасывание дробной части; до ближайшего целого, не большего Х; до ближайшего целого);

mod(X,Y) - остаток от деления X на Y;

sign(X) - знак числа (для комплексных X / |X|);

gcd(m,n) -наибольший общий делитель для целых чисел; если использовать оператор [g,c,d]=gcd(m,n), то дает указанный делитель и множители c,d такие, что g==m*c+n*d:

>> f=gcd(18,27)	f = 9
>> [g,c,d]=gcd(18,27)	g = 9	c = -1	d = 1;

lcm(m,n) - наименьшее общее кратное:

>> lcm(34,51)

ans = 102;

rat(X), rat (X,k) - представление цепной дробью с точностью |X|·10^-k/2 (по умолчанию |X|·10^-6):

>> rat(12.5)	ans =13 + 1/(-2)
>>rat(12.546)	ans =13 + 1/(-2 + 1/(-5 + 1/(15)));

rats(X), rats(X,k) - представление отношением целых чисел:

>> rats(12.546)

ans = 2045/163;

sqrt(X) - квадратный корень:

>> sqrt(5)	ans = 2.2361
>> sqrt(3+4i)	ans = 2.0000 + 1.0000i;

exp(X) - экспонента e^x (e^x+iy= e^x(cos y+i siny)):

>> exp(1)	ans = 2.7183
>> exp(2+i)	ans = 3.9923 + 6.2177i;

pow2(X) - двоичная экспонента 2^x;

log(X) - натуральный логарифм;

log2(X), log10(X) -логарифм по основанию 2 и основанию 10;

sin(X) cos(X) tan(X) cot(X) csc(X) sec(X) - тригонометрические функции (синус, косинус, тангенс, котангенс, косеканс, секанс):

sin(x+iy)=sin(x) ch(y) +i cos(x) sh(y); cos(x+iy)=cos(x) ch(y) -i sin(x) sh(y),
tg (X)= sin(X)/ cos(X); ctg(X)=cos(X)/sin(X);
cosec(X)=1/sin(X); sec(X)=1/ cos(X):

>> sin(pi/2)

ans= 1;

>> sin(3+4i)

ans = 3.8537 -27.0168i;

asin(X) acos(X) atan(X) acot(X) acsc(X) asec(X) - обратные тригонометрические функции (арксинус, арккосинус и т.д.):

>> asin(1/sqrt(2))

ans = 0.7854;

>> asin(3+4i)

ans = 0.6340 + 2.3055i;

atan2(Y,X) - круговой арктангенс Arctg (только для действительных частей аргументов), берется в интервале [-p,p ];

sinh(X) cosh(X) tanh(X) coth(X) csch(X) sech(X) - гиперболические функции (синус, косинус, тангенс, котангенс, косеканс, секанс): sh(X)=(e^X-e^-X)/2, ch(X)=(e^X+e^-X)/2 и др.;

asinh(X) acosh(X) atanh(X) acoth(X) acsch(X) asech(X) - обратные гиперболические функции:

,
,,
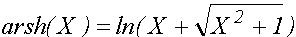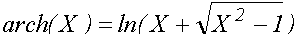
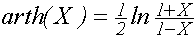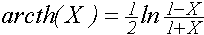arcsch(X)=arsh(1/X), arsech(X)=arch(1/X);

erf (Х) - интеграл вероятностей (функция Гаусса, функция ошибок)

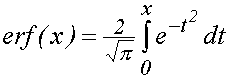
и родственные функции:

erfc(х) =1-erf(x) (дополнительный интеграл вероятностей);

erfcx(х) =exp(x²)·erfc(x) (нормированный дополнительный интеграл вероятностей);

erfinv(х) (аргумент, для которого интеграл вероятностей равен х);

gamma(х) -гамма-функция 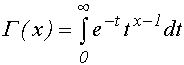(при целочисленных х Г(1+х)=х!)

>> gamma(5)	ans = 24
>> gamma(0)	Warning: Divide by zero (деление на нуль).
ans = Inf (неопределенное значение)
>> gamma(0.5)	ans = 1.7725
>> gamma(-0.5)	ans = -3.5449
>> gamma(0.1)	ans = 9.5135

и родственные функции:

gammainc (x,a)= 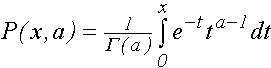(неполная гамма-функция);

gammaln (x)=ln Г(х) (логарифмическая гамма-функция);

beta (x,y) - бета-функция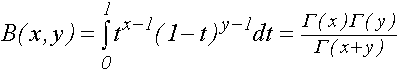
и родственные ей неполная и логарифмическая бета-функции;

функции преобразования координат:
из декартовых (X,Y) в полярные (r,j): r=(X²+Y²)^1/2, j=Arctg(Y/X) - [j,r]=cart2pol(X,Y);
из декартовой системы (X,Y,Z) в цилиндрическую (r,j,Z) - [j,r,Z]=cart2pol(X,Y,Z);
из декартовой системы в сферическую (r,j,q): r=(X²+Y²+Z²)^1/2, j=Arctg(Z/ (X²+Y²)^1/2), q=Arctg(Y,X) - [q,j,r]=cart2sph(X,Y,Z);
из полярной и цилиндрической в декартову (pol2cart): X=r·cos(j), Y=r·sin(j); из сферической в декартову (sph2cart): Z=r·sin(j), X=r·cos(j)·cos(q), X=r·cos(j)·sin (q) (эти функции незаменимы при графических отображениях результатов анализа, хотя многое из их графики уже предлагается среди готовых библиотечных средств);

специальные функции (цилиндрические функции Бесселя, Неймана, Ханкеля; функции Эйри, эллиптические функции Якоби и эллиптические интегралы, интегральная показательная функция, присоединенные функции Лежандра и много других функций, полезных при изучении физических процессов),

функции линейной алгебры, аппроксимации данных, численного интегрирования, поиска корней уравнений, обслуживания графики, обработки дат, множеств и др.

Если вы имеете намерение познакомиться с поведением какой-то из функций, поступите по аналогии с примитивным примером:

>> t=-pi:0.01:pi;	% значения аргумента от -p до p с шагом 0.01 (без вывода на экран);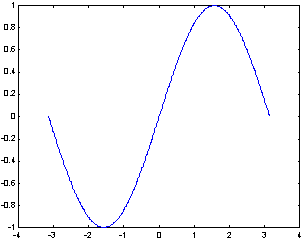
>> e=sin(t);	% массива значений функции;
>> plot(t,e)	% построение графика функции.

3. Режим программирования Для перехода в режим программирования в окне управления выбираем пункт File и входим в редактор MatLab'а: New (создать новый М-файл) или Open(открыть существующий файл с расширением.m). Открывается окно редактора Editor. В дальнейшем может производиться обычный набор текста программы или его корректура и действия в соответствии с меню (сохранение под текущим или другим именем, запуск на исполнение в обычном и отладочном режимах и др.). Различают два вида М-файлов: М-сценарии и М-функции. М-сценарий - это файл, содержащий последовательность команд и комментариев (строк, начинающихся символом %) и пользующийся данными из рабочей области. Заголовок его начинается командой script или может отсутствовать. Для М-функции допускаются входные и выходные аргументы, локализация внутренних ее переменных и возможность обращения к ней из других программ. М-функции включаются в библиотеку функций системы в виде текстовых файлов. Заголовок М-функции имеет вид: function [<список выходных переменных>]= <имя функции> (<список входных переменных>) например, функция вычисления факториала положительного числа и его обратной величины может быть описана файлом fact.m: function [f,g]=fact(n) % факториал и обратная величина f=prod (1:n); g=1/f; Кроме использованных выше операторов присваивания, программирование в MatLab'е допускает и ряд других традиционных для прогрммных сред операторов. Условный оператор выступает в одной из следующих форм: if <условие> if <условие> if<условие> <команды> <команды> <команды>end else elseif <условие> <команды> <команды> end else <команды> end В роли условия может использоваться любое логическое выражение, построенное на основе операций отношения и логических. Если значение этого выражения является массивом, то условие считается ис-тинным, если все его элементы истинны (истина - 1, ложь - 0). Оператор цикла с заданным числом повторений, в основном используемый в форме: for V=A:H:B for V=A:B <команды> <команды>end end (V -переменная/параметр цикла, A,B - начальное и конечные значения; H - приращение, по умолчанию 1). Допускаются и вложенные циклы, например: for i=1:n for i=1:n-1 for j=1:m for k=i+1:n a(i,j)=x(i)^j; if a(i) < a(k) end m=a(i) end a(i)=a(k) a(k)=m end end end В заголовке цикла можно использовать одномерный массив. Так цикл k=1;for i=[0 5 7] x(k)=2^i; k=k+1; end формирует массив Х=[1 32 128]. Оператор цикла с предусловием имеет традиционную конструкцию: while <условие> <команды> end и обеспечивает выполнение команд тела цикла, пока истинно проверяемое условие. Заметим, что работа цикла может быть прервана (выход из внутреннего цикла) оператором break: while a<1 n=n+1 if n>250 break end... Оператор переключения обобщает условный оператор на случай более двух условий и имеет конструкцию: switch <выражение> case <значение 1> <команды> case <значение 2> <команды>..... otherwise % может отсутствовать <команды> end Контрольные значения проверяются на равенство и могут задаваться и списком: switch k case {0} t=1 case {1, 2,5} t=2 otherwise t=0 end Выход из функции в вызывающую программу обеспечивается выполнением последнего ее оператора или командой return. Кроме упомянутых основных операторов, традиционных для любой системы программирования, остановимся на ряде операторов обеспечения пользовательского интерфейса. Ввод с клавиатуры реализуется командой вида <переменная>= input ('подсказка') Например, " x=input(' степень полинома '); степень полинома 3 Приостановка выполнения программы может быть предусмотрена включением в текст команды pause (приостановка до нажатия любой клавиши), pause (n) (приостановка на n сек),keyboard (приостановка с возможностью выполнять практически любые команды и последующим возвратом в программу командой return). Можно построить выбор варианта с клавиатуры созданием меню: <переменная>=menu ('заголовок','выбор1','выбор2',...) Например, команда: k=menu('Использовать метод','Гаусса','Краута','простой итерации') создаст на экране всплывающее меню с указанными пунктами-клавишами и щелчок по клавише задаст значение переменной k, рав-ное 1, 2 или 3. Мы не останавливаемся на многообразии операторов, связанных с выводом на экран (вывод значения disp, форматированный вывод fprint), отладкой и сигнализацией об ошибках, анализом списка аргументов и др. Приведем несколько простейших примеров использования программного режима. 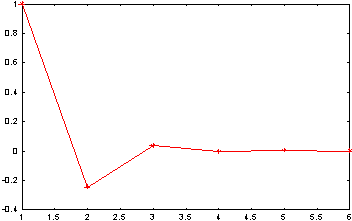Пример 1.Анализ скорости убывания элементов числовой последовательности 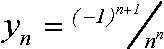до значений, меньших 0.0001) Чтобы с легкостью отыскивать значения элементов последовательности, опишем функцию (файл y.m): function f=y(n) if mod(n,2)==0 f=-1; else f=1; end f=f/n^n; end и сценарий (файл limit1.m): n=1;while abs(y(n))>1e-4 n=n+1;enddisp('Число элементов последовательности равно') k=nfor x=1:k Y(x)=y(x);enddisp('Значения элементов последовательности') Y plot(1:k,Y, 'r^-*') %Линия -сплошная(-)красная ®, маркеры(*)

Теперь можно в командной строке набрать вызов limit1, получая на экране число элементов последовательности k, значения элементов последовательности Y (n=1ёk) и "график" функции:

Число элементов последовательности равно k =6 Значения элементов последовательности

Y =

1.0000

-0.2500

0.0370

-0.0039

0.0003

-0.0000

Пример 2. Поиск оценки суммы ряда.

с точностью 10-6.

Файл limit2.m (сценарий): y=1; s=y; m=1; while abs(y)>1e-6 y=-y*(2*m-1)/(2*m+1).^2; s=s+y; m=m+1; end disp('Число слагаемых') disp(m-1) disp('Оценка суммы') disp(s)

В командной строке набираем limit2, получая на экране число элементов отрезка суммы, превышающих 10^-6 и саму оценку суммы:

Число слагаемых
Оценка суммы	0.90097107966794

наверх

следующая глава

Дата добавления: 2014-01-05