Решение основных задач линейной алгебры

При реализации многих задач, связанных с матричной алгеброй, полезными могут оказаться функции для оценок основных характеристик:

det(A) - определитель квадратной матрицы;

rank(A) - ранг матрицы;

trace(A) - след матрицы (сумма элементов главной диагонали);

>> A=[1 2 3; 5 4 3; 3 4 3]

A =

>> det(A) ans =12

>> rank(A) ans = 3

>> trace(A) ans = 8

Выше среди операций системы мы уже упоминали операцию транспонирования матрицы:

>> A=[ 1 2 3; 23 11 0]

A =

>> B=A'

B =

и возведения в степень (матричного умножения на себя или инверсии):

>> A=[1 2 3; 5 4 3; 3 4 3]

A =

>>D=A^(-1)

D =
	-0.0000	0.5000	-0.5000
	-0.5000	-0.5000	1.0000
	0.6667	0.1667	-0.5000

>> A^0

ans =

При решении многих задач (например, при оценке сходимости методов) используется понятие нормы вектора (матрицы). В рас-сматриваемой системе для поиска нормы предлагается функции norm(A) и norm(A, k).

Если А - вектор, то норма определяется (по умолчанию k=2)

;

при k=inf и k=-inf соответственно |A|= max(|A_i|) и |A|= min(|A_i|);

>>v=[3 4 -10] v = 3 4 -10	>> norm(v) ans = 11.1803	>> norm(v,2) ans = 11.1803	>> norm(v,inf) ans = 10	>>norm(v,-inf) ans = 3
	>> norm(v,1) ans = 17 >>	norm(v,-1) ans = 1.4634	>>norm(v,3) ans = 10.2946	>>norm(v,'fro') ans = 11.1803

Если А - матрица, то норма определяется только для k=1, 2, inf и fro (по умолчанию k=2):

k=1 - ;

k=2 - max(svd(A)) - максимальное из сингулярных чисел матрицы (значений квадратных корней из собственных чисел матрицы А ' А);

k=inf - 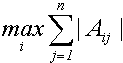; k='fro' -, B=A'*A:

A =

>> norm(A,1) ans = 10

>> norm(A) ans = 9.6871

>>norm(A,inf) ans = 12

>>norm(A,'fro') ans = 9.8995

Для задачи решения системы линейных алгебраических уравнений, одной из популярнейших в вычислительной математике, предусмотрены даже "элементарные" операции для подобной задачи.

Так для решения системы AX=B (A -матрица коэффициентов размерности mґn, B- матрица правых частей размерности n x k, Х - матрица из k векторов-столбцов решений) можно использовать команду обратного деления "\". Например, для решения системы

x1+2 x2+3 x3 = 3 (или 3)
5 x1+4 x2+3 x3 = 9 (или 9)
3 x1+4 x2+3 x3 = 6 (или 7)

задаем (построчно) матрицу коэффициентов и векторов правой части

>> A=[1 2 3; 5 4 3; 3 4 3]

A =

>> B=[3 3; 9 9; 6 7]

B =

и выполнить

>> X=A\B	X =1.5000	1.0000
0.0000	1.0000
0.5000

При решении системы XA=B можно воспользоваться операцией обычного деления. Так решение той же системы

>>X=B'/A'	X = 1.5000	-0.0000	0.5000
1.0000	1.0000

(обратите внимание на строчное представление решений).

Под кажущейся простотой решения скрывается достаточно серьезный анализ структуры матрицы и использование лучшего по точности и быстродействию алгоритма (метод Гаусса, разложение Холецкого и др.)

Для прямоугольной матрицы А (m№n) решение строится по минимуму квадрата ошибки (используется QR-разложение на основе преобразований Хаусхолдера) и не сопровождается сообщениями о множественности решений или переопределенности системы:

одно уравнение с 3 неизвестными:

>> a=[1 2 3];
>>b=6;
x=a\b
x = 0

три уравнения с 2 неизвестными:

>> c=[1 2; 3 7; 2 5];

>> d=[3; 10; 9];

>> x=c\d

x = -5.00000000000002

3.66666666666667

Естественно, что квадратная матрица коэффициентов должна быть невырожденной (определитель отличен от нуля) и в противном случае выдается сообщение Matrix is singular to working precision и элементы решения принимают значения inf (не определено).

Особого упоминания заслуживает обращение (инверсия) матрицы, для которого предусмотрена операция возведения в степень -1 и функция inv(A):

>> A=[1 2 3; 5 4 3; 3 4 3]

A =

>> C=inv(A)

C =
-0.0000	0.5000	-0.5000
-0.5000	-0.5000	1.0000
0.6667	0.1667	-0.5000

>> D=A^(-1)

D =
-0.0000	0.5000	-0.5000
-0.5000	-0.5000	1.0000
0.6667	0.1667	-0.5000

Напомним, что обращение матрицы может оказаться полезным при решении системы AX=B в виде X=A^-1B:

>> B=[3 3; 9 9; 6 7]

B =

>> X=inv(A)*B

X =	1.5000	1.0000
	1.0000
0.5000	0.0000

При решении линейных систем и других задач интересно пред-ставление матрицы разложением на матрицы упрощенной структуры.

[L,U]=lu(A) - дает т.н. LU-разложение произвольной квадратной матицы в виде произведения нижней и верхней треугольных матриц A=LU (в матрице L возможны перестановки); такое представление позволяет, в частности, решение системы АХ=В свести к двум простым системам LZ=B, UX=Z.

[L,U,P]=lu(A) - дает LU-разложение c выводом матрицы перестановок Р такой, что PA=LU.

A =

>> [L,U]=lu(A)

L =
0.2000	0.7500	1.0000
1.0000
0.6000	1.0000

U =
5.0000	4.0000	3.0000
	1.6000	1.2000
		1.5000

>> [L,U,P]=lu(A)

L =
1.0000
0.6000	1.0000
0.2000	0.7500	1.0000

U =
5.0000	4.0000	3.0000
	1.6000	1.2000
		1.5000

P =

R=chol(A), [R,p] =chol(A) - дает разложение Холецкого для по-ложительно определенной симметрической матрицы A=RўR, где R - верхняя треугольная матрица. Если матрица А не является положительно определенной, то в первом варианте возникает сообщение об ошибке и во втором R - матрица порядка q=p-1:

C =

R=chol(С)??? Error using ==> chol Matrix must be positive definite

>> [R,p]=chol(С)

R =

p = 3

В приведенном примере лишь первые два главных минора положительны (det(С)= -3) и, соответственно, q=2 и RўR дает второй главный минор матрицы С.

[Q,R]=qr(A), [Q,R,P]=qr(A), [Q,R]=qr(A,0) находит QR-разложение для прямоугольной матрицы размерности m x n:

[Q,R]=qr(A) - в виде A=QR произведения унитарной матрицы Q (Q*Q'=E) и верхней треугольной матрицы R:

C =

>> [Q,R]=qr(С)

Q =	-0.2672	-0.0514	-0.9622
-0.5345	-0.8229	0.1924
-0.8017	0.5657	0.1924

R =	-3.7416	-7.2160	-9.0868
	-1.3887	-0.3086
		-0.5773

t =

>>[Q,R]=qr(t)

Q =	-0.1961	-0.9805
-0.9805	0.1961

R =

-5.0990	-3.5301	-1.9611
	-2.3534	-4.7068

[Q,R,P]=qr(A) отличается от предыдущего упорядочением по убыванию модулей диагональных элементов R и наличием соответст-вующей матрицы перестановок Р (A*P'=Q*R);

[Q,R]=qr(A,0) при m>n отличается тем, что вычисляются лишь n столбцов матрицы Q.

Если после выполнения QR-разложения выполнить команду [Q1,R1]=qrdelete(Q,R,k), то будет выполнен пересчет матриц для варианта, когда в матрице А удален k-й столбец. Если после QR-разложения выполнить команду [Q1,R1]=qrdelete(Q,R,k,X), то будут пересчитаны матрицы для варианта, когда в матрице А перед столбцом k вставлен столбец Х.

X=nnis(A,B), X=nnis(A,B,t) позволяют искать решение системы АХ=В методом наименьших квадратов, где отыскиваются неотрицательные решения Х, минимизирующие norm(A*X-B) или гарантирующие точность e при задании t=max(m,n)*norm(A,1)* e.

Особое место в библиотеке занимают средства для вычисления собственных чисел и векторов.

В простейшем варианте отыскиваются ненулевые решения системы АХ=lX командами d=eig(A) или [X,d]=eig(A) (d- диагональная матрица собственных чисел, Х -матрица из нормированных собственных векторов):

a =

>>d=eig(a) d =

0.2179

1.8393

29.9428

>> [R,d]=eig(a) R =

0.8484	0.7163	-0.1198
-0.5150	0.6563	-0.3295
0.1222	-0.2371	-0.9365

d =

0.2179
	1.8393
		29.9428

Для проверки качества поиска (при значительных размерностях и многочисленных особых случаях такая проверка весьма желатель-на) достаточно проверить на близость к нулю значений A*X=R*D:

>>a*R-R*d
ans = 1.0e-014 *
0.0583	0.0666	-0.7549
0.0166	-0.0444	-0.5329
0.0902	-0.3886	-0.7105

Функции d=eig(A,B) и [V,D]= eig(A,B) позволяют решать полную (обобщенную) проблему собственных значений АХ=lBX.

Решение задачи осуществляется на основе QR-алгоритма и его модификаций и при числе итераций, превышающем 30Ч n, может быть прервано с сообщением Solution will not converge (решение не сходится).

Проблему собственных значений можно решать и для матричного полинома (A₀+lA₁l²A₂+...+l^pA_p)X=0 командой [R,d]=polyeig(A₀,A₁,.., A_p), где R- матрица размера n x (n x p) собственных векторов. При р=0 эта функция тождественна eig(A₀), при р=1 - eig(A₀,-A₁) и в случае матриц с n=1 (скаляров) - roots (A_p,...,A₁,A₀), то есть ищет корни уравнения A_pl^p+...+ A₂l² +A₁l +A₀=0.

Для решения ряда задач используется функция сингулярного разложения матрицы в формах s=svd(A), [U,S,V]=svd(A), [U,S,V]=svd(A,0) - матрица А размерности m x n (mіn) представляется в виде A=U*S*Vў, где Uў*U=V*Vў=E, S=diag(s₁,s₂,...,s_n). Здесь U состоит из n собственных векторов для n наибольших собственных зна-чений матрицы ААў, а V - из ортонормированных собственных векторов матрицы АўА; на диагонали матрицы S - значения квадратных корней из собственных чисел матрицы АўА (сингулярные числа).

наверх

следующая глава

Дата добавления: 2014-01-05