
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аппроксимация и интерполяция
|
|
|
|
polifit(X,Y,n) - аппроксимация функции Y=Y(X) полиномом n-й степени:
| >> X=0:0.1:0.5; | |
| >> F=X.*sin(X); | |
| >> P=polyfit(X,F,1) | |
| P = 0.4814 -0.0314 | % P(x)= 0.4814 x -0.0314 |
| >> FF=polyval(P,X) | |
| FF = -0.0314 0.0168 0.0649 0.1130 0.1612 0.2093 | |
| >> plot(X,F,'ob', X,FF,'-g'),grid,axis([0 0.5 -0.05 0.25]) % рис.8.2 |
interpft(Y,n,dim) -аппроксимация периодической функции на основе быстрого преобразования Фурье (Y - одномерный массив значений функции;
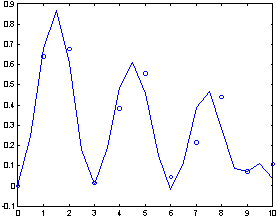 Рис.8.3. Рис.8.3.
| n - число узлов в массиве значений): >> X=0:10; >> Y=sin(X).^2.*exp(-0.1.*X); >> YP=interpft(Y,21); >> xp=0:0.5:10; >> plot(X,Y,'ob', xp,YP) % Рис. 8.3 Заметим, что в библиотеке имеется богатый ассортимент средств для преобразования Фурье. |
spline(X,Y,Z) - интерполяция Y=Y(X) кубическим сплайном и вывод соответствующих значений в точках Z. Для получения большей информации используется конструкция pp=spline(X,Y): здесь командой V=ppval(pp,Z) можно найти значения в точках Z, a командой [Xs, Coef, m,L]=unmkpp(pp) получить данные о векторе разбиений аргумента Xs, коэффициентах Coef, m=length(Xs), L=length(Coef)/m.
interp1(X,Y,Z), interp1(X,Y,Z,'method') - одномерная табличная интерполяция (если Y двумерный массив, интерполяция ведется по каждому столбцу; значения Z должны входить в диапазон значений Х). Можно указать метод интерполяции - кусочно-линейной (linear, по умолчанию), ступенчатой (nearest), кубической (cubic), кубическими сплайнами (spline). Функция interp1q(X,Y,Z) реализует быструю линейную интерполяцию на неравномерной сетке.
interp2(X1,X2,Y,Z1,Z2), interp1(X1,X2,Y,Z1,Z2,'method') - двумерная табличная интерполяция Y=Y(X1,X2), аргументы должны меняться монотонно и заданы в формате функции meshgrid.

Рис.8.4.
>> [X1,X2]=meshgrid(-1:0.1:1);
>> Y=exp(-X1.^2-X2.^2).*(1+X1+X2);
>> [Z1,Z2]=meshgrid(-1:0.05:1);
>> Y2=interp2(X1,X2,Y,Z1,Z2);
>> mesh(X1,X2,Y),hold on,mesh(Z1,Z2,Y2+2),hold off % Рис. 8.4
interp3(X1,X2,X3,Y,Z1,Z2,Z3), interp3(..., 'method') - трехмерная табличная интерполяция Y=Y(X1,X2,X3);
interpn(X1,X2,...,Y,Z1,Z2,...), interp3(..., 'method') - многомер-ная табличная интерполяция Y=Y(X1,X2,...);
griddata(X1,X2,Y,Z1,Z2), griddata(X1,X2,Y,Z1,Z2, 'method') - двумерная табличная интерполяция на неравномерной сетке.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 504; Нарушение авторских прав?; Мы поможем в написании вашей работы!