
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над полиномами
|
|
|
|
Рассмотрим полином вида Pn(x)=p1xn+p2xn-1+...+pnx+an+1. Соответственно будем обозначать Р - n+1-мерный вектор коэффициентов, Х - массив значений аргумента.
При вычислении значений полинома для элементов массива можно использовать функцию polyval(P,X):
>>polyval([1 2 5],[0 3 1])
| >> polyval([1 2 5],[0 3 1; 1 1 1])
|
С помощью функции polyvalm(P,X) можно вычислять значения матричного полинома для квадратной матрицы Х:
| >> polyvalm([1 2 5],[0 3 1; 1 1 1; 0 0 2]) | |||
| ans = | |||
Умножение полиномов Сm+n(x)=Pm(x) x Qn(x) выполняется командой C=conv(P,Q) -
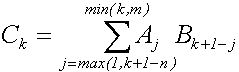
Деление полиномов можно реализовать командой [C,R]=deconv(A,B), где С -частное и R - остаток от деления А на В.
>> conv([1 2 3],[5 6])
| [c,r]=deconv([1 2 3],[5 6])
|
Вычисление производных от полинома, произведения и отношения полиномов производится соответственно командами dp=polyder(P), dc=polyder(A,B) и [f,g]=polyder(A,B):
polyder([1 -2 3 4 5])
| >> polyder([1 2 3],[5 6])
| >> [f,g]=polyder([1 2 3],[5 6])
|
Вычисление корней полинома реализуется функцией roots(P), а построение полинома по его корням - функцией poly(R).
| >> r=roots([1 3 5 7]) r = -2.1795 -0.4102 + 1.7445 i -0.4102 - 1.7445 i | >>poly(r)
| ||||||
Функция poly(А) обеспечивает построение характеристического полинома |lE-A|=0 (см. проблему собственных значений):
| >> A= magic(3) | |||
| A = | |||
| >>P=poly(A) | |||
| P = | |||
| 1.0e+002 * | |||
| 0.0100 | -0.1500 | -0.2400 | 3.6000 |
В приложениях, особенно связанных с преобразованием Лапласа при решении дифференциальных уравнений, оперируют с отношениями полиномов и представлениями их в виде простых дробей:
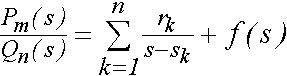 ,
,
где sk - простые корни полинома Qn(s); если некоторый корень sj имеет кратность m, то соответствующее слагаемое представляется в виде,
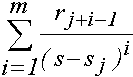
Команда [r,s,f] =residue(P,Q) дает разложение отношения полиномов на простые дроби (в случае близких корней возможна значительная погрешность). В случае кратного корня пользуются функцией rj=resi2(P,Q,sj,m,j), где j -номер вычисляемого коэффициента (по умолчанию j=m); по умолчанию m=1 (простой корень).
Команда [P,Q] =residue(r,s,f) выполняет обратное действие свертки разложения в отношение полиномов.
Выполнив действия
|
|
видим, что
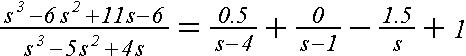
В случае кратного корня
|
|
видим разложение:
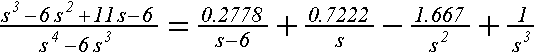
наверх
следующая глава
8. Анализ и обработка данных
8.1. Обработка статистических данных 8.2. Численное дифференцирование 8.3. Аппроксимация и интерполяция 8.4. Численное интегрирование 8.5. Нули и экстремумы функций 8.6. Обыкновенные дифференциальные уравнения
8.1 Обработка статистических данных
Никакой анализ статистических данных не может обойтись без предварительной их обработки:
max (A), min(A) - поиск экстремальных элементов по столбцам массива А;
max(A,B), min(A,B) - формирование массива с элементами, равными экстремальным из соответствующих элементов массивов;
max(A,[ ],dim), min(A,[ ],dim) - вектор экстремальных элементов по измерению dim;
[C,I]=max(...), [C,I]=min(...) - дополнительно выводится строка индексов экстремальных элементов;
median(X), median (X,dim) - медианы массива;
mean(X), mean (X,dim) -средние значения;
std(X), std(X,flag), std(X,flag,dim) - стандартное отклонение (flag=0 -несмещенная оценка s; flag=1 - смещенная оценка s):
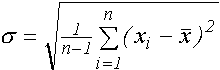 ; ; 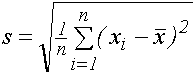 ;
cov(X, Y), cov(X,Y, flag) - ковариация для для массивов Х и Y (каждый столбец - переменная, строка - наблюдение) ;
cov(X, Y), cov(X,Y, flag) - ковариация для для массивов Х и Y (каждый столбец - переменная, строка - наблюдение)
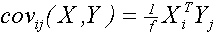 , f=n или n-1;
cov(X), cov(X,flag) - ковариация для столбцов массива Х;
corrcoef (X), corrcoef (X,Y) -коэффициенты корреляции: , f=n или n-1;
cov(X), cov(X,flag) - ковариация для столбцов массива Х;
corrcoef (X), corrcoef (X,Y) -коэффициенты корреляции:
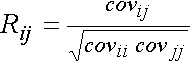 .
8.2. Численное дифференцирование
Как известно, численное дифференцирование строится на использовании аппарата конечных разностей и соответствующего многообразия аппроксимаций. Здесь полезны функции:
diff(X), diff(X, n), diff(X, n, dim) - вычисление конечных разностей (первых, n-го порядка или по указанному измерению); если Х -массив, берутся разности между столбцами: .
8.2. Численное дифференцирование
Как известно, численное дифференцирование строится на использовании аппарата конечных разностей и соответствующего многообразия аппроксимаций. Здесь полезны функции:
diff(X), diff(X, n), diff(X, n, dim) - вычисление конечных разностей (первых, n-го порядка или по указанному измерению); если Х -массив, берутся разности между столбцами:
Для задач оптимизации градиентными методами полезны функции: gradient(F), gradient(F,h), gradient(F,h1,h2,...) -приближенная оценка градиента функции n переменных с автоматическим выбором шага или с указанным шагом (одинаковым или разным по переменным):
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 859; Нарушение авторских прав?; Мы поможем в написании вашей работы!
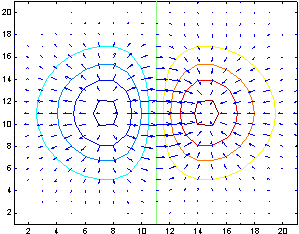 Рис.8.1.
Рис.8.1.
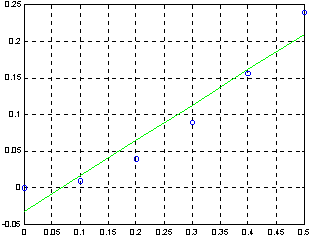 Рис.8.2.
Рис.8.2.