Турбулентное течение вблизи твердой стенки

Расчет турбулентного течения в трубах относится к широко распространенным инженерным задачам. Одним из важных элементов расчета является нахождение закона распределения осредненных скоростей в поперечном сечении безграничной плоской трубы.

По Прандтлю, поток вблизи стенки при турбулентном течении условно разбивается на две области (двухслойная модель Прандтля): турбулентное ядро, в котором определяющими являются турбулентные напряжения Рейнольдса, и тонкий вязкий подслой (ламинарный, либо пристенный подслой), непосредственно прилегающий к стенке, в котором влияние турбулентности, наоборот, мало, а касательные напряжения обусловлены молекулярной вязкостью в соответствии с законом трения Ньютона.

На рисунке слева приведен примерный вид поля осредненных скоростей (эпюра скорости) при турбулентном течении в трубопроводе. Следует обратить внимание на большую заполненность эпюры (большую равномерность) по сравнению с соответствующим профилем для ламинарного течения. Это объясняется тем, что вследствие интенсивного перемешивания частиц жидкости за счет турбулентных пульсаций происходит обмен количеством движения между слоями и, как следствие, более равномерное распределение скоростей в поперечном сечении.

В непосредственной близости от стенки в пределах пристенного подслоя решающее влияние на течение оказывают жесткость стенки, ее непроницаемость и свойство прилипания частиц жидкости. На самой стенке справедливы условия:

, ; .

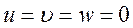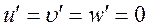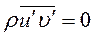Таким образом, для области в пределах вязкого подслоя можно записать:

где - касательное напряжение на стенке, отбрасывая черточки, обозначающие осреднение (здесь, и в дальнейшем). Заметим, что в этом случае напряжение трения между любыми слоями в осредненном движении постоянно и равно напряжению трения на стенке.

Интегрирование этого выражения дает линейный профиль скоростей у стенки:

,

Учитывая, что при 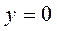, , 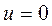получим . Следовательно:

Имея в виду, что 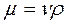, после подстановки получаем

Величина 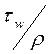имеет размерность квадрата скорости, хотя по своей природе состоит из динамических величин: напряжения и плотности. По этой причине корень квадратный из нее, т.е.

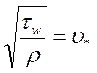
называют динамической скоростью, либо скоростью трения. Подставляя выражение для динамической скорости в предыдущую формулу, получим:

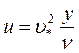, или

На границе ламинарного подслоя , т.е.

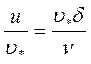
В правой части стоит безразмерное выражение, аналогичное числу Рейнольдса, построенному по динамической скорости и толщине подслоя. Согласно тщательным опытам И. Никурадзе, эта величина приближенно равна 11,5; тогда для оценки толщины ламинарного подслоя получается выражение:

Очевидно, что этим соотношением можно воспользоваться лишь в случае, если известна динамическая скорость.

Перейдем теперь к установлению закона распределения осредненных скоростей в турбулентном ядре потока. В этой области определяющую роль играют турбулентные касательные напряжения, и, следовательно, можно воспользоваться формулой Прандтля с использованием длины пути смешения:

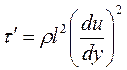
Замечая, что расстояние y данной точки потока от поверхности есть единственная характерная для потока длина, Прандтль положил путь смешения пропорциональным y, т.е. l =ky, где коэффициент пропорциональности k представляет некоторую постоянную, численное значение которой определяется из опыта (выполненные измерения показывают, что ).

Для дальнейшего необходимо также сделать предположение о распределении турбулентных касательных напряжений в рассматриваемой области течения. Вообще говоря, они являются величинами переменными, однако, в области, расположенной достаточно близко к стенке, величины касательных напряжений изменяются незначительно, и можно полагать их постоянными и равными касательному напряжению на стенке, т.е. .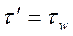

При этих допущениях формула Прандтля принимает вид

,

или, вводя динамическую скорость:

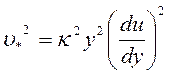
Преобразуя полученное выражение и разделяя переменные, получаем дифференциальное уравнение:

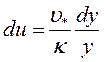
и после интегрирования:

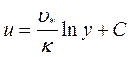
Таким образом, линейный профиль скоростей при ламинарном движении в подслое трансформируется в логарифмический для турбулентного движения в ядре потока. При определении постоянной интегрирования С нельзя использовать граничное условие на стенке, поскольку в непосредственной близости от стенки полученное уравнение несправедливо, а там имеет место линейный профиль скорости. Единственной возможностью определения этой постоянной является сращивание полученного решения с линейным.

На границе ламинарного подслоя (со стороны турбулентного ядра) имеем: 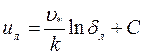, где δ_л – толщина подслоя, u_л – скорость на его границе. С другой стороны, из линейности профиля вблизи стенки, следует, что: , где 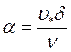– постоянная, характеризующая число Re, построенное по толщине подслоя и динамической скорости (измерена в опытах И. Никурадзе и составляет α ≈ 11,5). Отсюда величина постоянной С определится как:

,

Подставляя это значение в формулу для профиля скорости, получим:

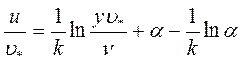
Переходя от натуральных логарифмов к десятичным и подставив численные значения постоянных α ≈ 11,5 и к ≈ 0,4, получим универсальный закон распределения скоростей вблизи твердой стенки при турбулентном режиме течения:

Принципиальное значение имеет тот факт, что логарифмическая формула сохраняет свою форму для всех чисел Re, или, как принято говорить, универсальна. Структура ее такова, что влияние числа Рейнольдса, т.е. вязкости, полностью входит в масштабы длин 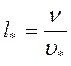и скоростей ; это и делает формулу универсальной. Поэтому вышеуказанные масштабы принято называть универсальными. Строго говоря, полученное соотношение выводится для плоских труб, но опыт показывает, что оно оказывается справедливым и для круглых, что подтверждает экспериментально установленный факт о независимости распределения скорости от причин, обусловливающих возникновение касательных напряжений (вязкости, шероховатости). Константы k и α представляют две основные эмпирические постоянные, характеризующие турбулентное движение. Применяя вышеуказанный закон распределения скоростей к оси трубы, где u=u_max, а y=R, и произведя почленное вычитание полученных соотношений, придем к выражению для профиля скоростей:

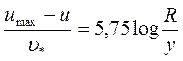
Таким образом, проведенный упрощенный теоретический анализ позволяет выявить основные закономерности распределения скоростей при турбулентном движении в круглой трубе.

Использование двухслойной модели, т.е. разделение потока на турбулентное ядро и пристенный ламинарный подслой, приводит к специфической классификации стенок труб. Если толщина пристенного подслоя больше выступов шероховатости, трубы называют гидравлически гладкими, в противном случае - шероховатыми.

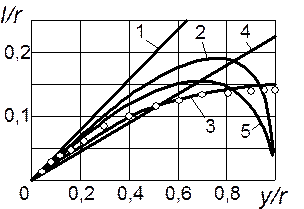
Заметим, что, гипотеза о пропорциональности пути смешения расстоянию от стенки не вполне согласуется с данными опытов. На нижеследующем рисунке приведены зависимости, характеризующие распределение длины пути перемешивания в поперечном сечении круглой трубы по данным опытов И.Никурадзе (кружки) и по формулам, предложенным различными авторами. В соответствии с результатами экспериментов, значение l достигает максимума на оси трубы. Из графика следует, что гипотеза Прандтля (прямая 1) не согласуется с опытными данными в области потока вблизи оси трубы.

.

Существенно отличаются также от опытных результатов выражения для длины пути смешения, предложенные другими авторами: Т.Карманом (кривая 2), Конаковым (кривая 4), Саткевичем (кривая 5). Достаточно близка к экспериментальным данным зависимость Альтшуля (кривая 3), описывающая длину пути перемешивания формулой:

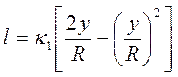
Очевидно одно – подход Прандтля, дающий возможность получить логарифмический профиль скоростей в турбулентном ядре, справедлив в области потока не слишком удаленной от стенки. Следует иметь в виду также несоответствие экспериментальным данным теоретических представлений о ламинарном подслое, как об области, в которой отсутствуют пульсации. Пульсации скорости и, в особенности, - давления проникают и в этот слой, но следуют там своим закономерностям. Не вполне обосновано и предположение о том, что в ядре потока физическая (молекулярная) вязкость не играет никакой роли. В то же время, предлагая формулы для распределения скоростей и толщины ламинарного подслоя, полуэмпирические теории дают возможность получить соотношения для расчетов сопротивления труб турбулентному движению жидкости, т.е. определяют связь между коэффициентом сопротивления λ и числом Рейнольдса , рассчитанным по среднерасходной скорости, диаметру трубы и кинематическому коэффициенту вязкости жидкости. В частности, с использованием логарифмического профиля скоростей была получена универсальная формула сопротивления, справедливая в весьма широком диапазоне чисел Re:

,

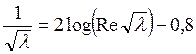численные значения коэффициентов в которой были уточнены по результатам многих опытов (λ - коэффициент гидравлического сопротивления, определение которого приведено в следующем разделе).

Наряду с выведенными полуэмпирическими соотношениями: логарифмическим профилем скоростей и логарифмической формулой сопротивления, большую роль продолжают играть чисто эмпирические степенные профили скоростей и формул сопротивления. К числу последних относится формула Блазиуса, которая представляет собой частный случай общей степенной формулы сопротивления: :

, применимость которой, как показывают результаты экспериментов, ограничена значениями Re < 10⁵ (т.е. областью так называемого гладкостенного течения – без проявления шероховатости поверхности).

Как показывают опыты, с возрастанием критерия Рейнольдса показатель степени m и коэффициент C в формуле сопротивления меняются, причем m – убывает. Пользуясь экспериментальной формулой Блазиуса, Карман из соображений размерности показал, что этому закону сопротивления соответствует степенной профиль скоростей:

,

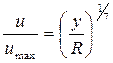получивший в дальнейшем наименование закона одной седьмой.

Точно также общей степенной формуле сопротивления соответствует степенной же закон распределения скоростей:

,

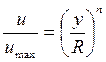причем можно установить связь между показателями степени m и n: .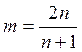

Как уже отмечалось, с возрастанием Re численные значения показателя степени уменьшаются. В частности, хорошо согласуются с опытом зависимости:

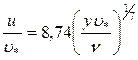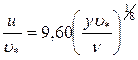при

при

Дата добавления: 2014-01-05