Предмет и метод экономической теории

Потери давления (напора) при турбулентном течении в трубах.

Напомним, что рассмотрение закономерностей как ламинарного, так и турбулентного течений в трубах помимо познавательных имеет в виду цели сугубо практические: - получить соотношения, определяющие законы сопротивления в трубопроводных сетях и создающие возможность выполнения инженерных гидравлических расчетов. Для ламинарного течения эта задача решается с помощью формулы Хагена-Пуазейля. Из рассмотрения особенностей турбулентного течения становится ясным, что вследствие его чрезвычайной сложности получение аналогичного соотношения чисто теоретическим путем в настоящее время невозможно.

Как было показано, выражение для турбулентных касательных напряжений (напряжений Рейнольдса) имеет вид: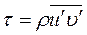

Из соображений размерности это позволяет утверждать, что существует связь между средней скоростью и касательным напряжением на стенке трубы вида: 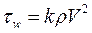, где k - коэффициент пропорциональности, V- среднерасходная (средняя) скорость. Аналогичная зависимость имеет место в определении так называемого коэффициента трения 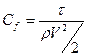, причем в принятых обозначениях.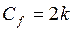

С другой стороны, из условия динамического равновесия движущегося под действием постоянного перепада давления Δ p жидкого цилиндра длиной l в трубе диаметром d: 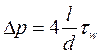, и после подстановки в это выражение связи напряжения трения на стенке со средней скоростью, получим: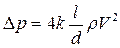, или .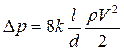

В такой форме записи выражение 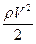имеет четкий физический смысл. Это так называемое динамическое давление потока, обусловленное средней скоростью, или кинетическая энергия потока, заключенная в единице объема.

Обозначим величину 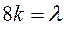(соответственно, получим, что: 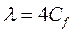) и назовем ее коэффициентом гидравлического сопротивления, тогда:

,

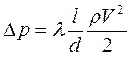(причем из условия динамического равновесия ),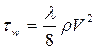

либо, используя определение напора, для несжимаемой жидкости (ρ = const):

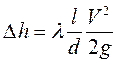
Полученное соотношение носит название формулы Дарси-Вейсбаха и является, по существу, определением коэффициента гидравлического сопротивления λ.

Ранее отмечалось, что если в преобразованной формуле Хагена-Пуазейля обозначить величину 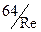буквой 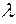, то она превращается в формулу Дарси-Вейсбаха. В этом смысле формула Дарси-Вейсбаха может быть признана универсальной, т.е. пригодной как для ламинарного, так и для турбулентного течений.

Закон сопротивления для турбулентного течения, полученный с помощью полуэмпирических теорий, использующий логарифмический профиль скоростей в турбулентном ядре потока и хорошо подтвержденный экспериментально, был приведен в предыдущем разделе.

.

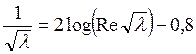Эта зависимость дает искомую связь 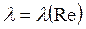в неявном виде, неудобном для использования. И.Никурадзе предложил пользоваться следующей степенной зависимостью, приведенной на рисунке:

,

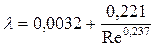и обеспечивающей хорошее совпадение с экспериментальными данными в широком диапазоне чисел Re. На том же рисунке приведена для сравнения зависимость 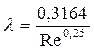, соответствующая широко используемой в гидравлике формуле Блазиуса. Отметим, что все кривые на рисунке построены в логарифмических координатах, т.е. в виде: 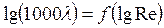. Таким образом, криволинейные степенные зависимости в этих координатах представляются прямыми, причем в левом нижнем углу пунктиром показана прямая, соответствующая закону сопротивления 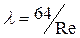при ламинарном движении.

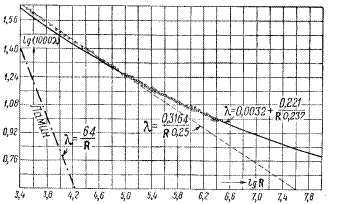
Результаты, представленные выше относились в основном к движению в гладкой трубе со строго цилиндрической поверхностью. На практике приходится иметь дело с более или менее шероховатыми трубами и с неточной цилиндричностью внутренней поверхности – волнистостью.

Несколько идеализируя и обобщая понятие шероховатости представим себе, что внутренняя поверхность трубы покрыта бугорками, имеющими вид зерен примерно одинакового размера. Условимся среднюю высоту бугорков шероховатости называть абсолютной шероховатостью, а отношение высоты бугорка к радиусу (или диаметру) трубы – относительной шероховатостью. В дальнейшем предполагается, что относительная шероховатость сравнительно невелика (не превышает 3-4%).

Рассмотрение типичных для труб с зернистой шероховатостью экспериментальных данных, полученных Никурадзе в опытах с искусственной песочной шероховатостью и показанных на приведенном ниже рисунке, дает возможность сделать определенные выводы:

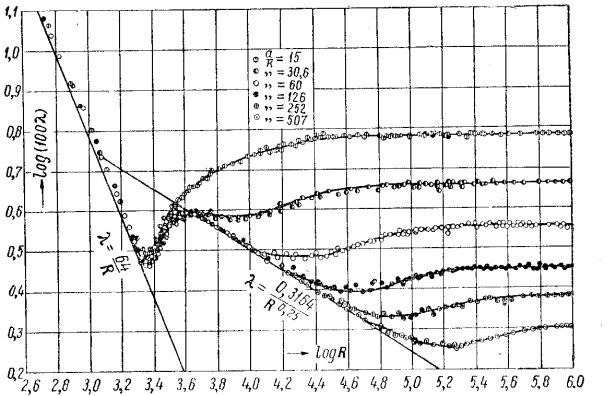
А именно:

· Относительная шероховатость не влияет на критическое число Re_кр. перехода ламинарного режима в турбулентный; для различных относительных шероховатостей кривые сопротивления сходят с уже известной нам прямой для ламинарного режима 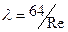при одном и том значении Re.

· Переходный режим также почти не зависит от относительной шероховатости.

· Чем меньше относительная шероховатость, тем в большем диапазоне чисел Рейнольдса наблюдается обычное турбулентное движение, соответствующее гладким трубам (зависимость Блазиуса).

· С возрастанием Re всегда наступает режим течения (при любой шероховатости), когда коэффициент сопротивления перестает зависеть от Re; причем, чем меньше относительная шероховатость, тем при больших значениях числа Рейнольдса это происходит. При этом численные значения коэффициента сопротивления растут вместе с шероховатостью.

Этим основным результатам можно дать наглядное теоретическое и истолкование, если сопоставить высоту бугорков шероховатости с толщиной ламинарного подслоя δ_л . Рассмотрим три случая:

Первый предельный режим: бугорки шероховатости погружены в ламинарный подслой, наличие этих бугорков не нарушает его ламинарности, обтекание их происходит без отрывов и вихреобразований. В этом случае с точки зрения гидравлического сопротивления нет разницы между гладкой и шероховатой трубами. Шероховатая труба является гидродинамически гладкой. Эксперименты показывают, что высота зерен Δ, образующих шероховатость, при этом удовлетворяет соотношению:

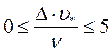, где 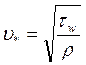- динамическая скорость, ν – коэффициент кинематической вязкости жидкости.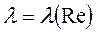

Второй предельный режим: бугорки шероховатости выходят за пределы ламинарного подслоя. Отрывное обтекание бугорков приводит к повышению сопротивления поверхности трубы из-за сопротивления их как плохо обтекаемых тел. Как известно, это сопротивление не зависит от Re и пропорционально квадрату скорости набегающего потока. Это режим можно назвать режимом развитой шероховатости (квадратичным режимом сопротивления). При этом размеры зерен шероховатости Δ соответствуют величинам, определяемым как: 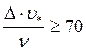, а коэффициент сопротивления λ = λ(Δ/d).

Промежуточный режим: когда высота бугорков шероховатости имеет примерно ту же величину, что и толщина ламинарного подслоя (шероховатость и толщина ламинарного подслоя – величины одного порядка), при этом элементы шероховатости частично выступают из ламинарного подслоя. По отношению к этому режиму оба рассмотренных выше являются предельными. В этом случае гидравлическое сопротивление труб зависит и от числа Рейнольдса, и от шероховатости поверхности: λ = λ(Δ/d, Re), а высота зерен шероховатости находится в диапазоне: .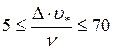

Таким образом, каждому значению числа Рейнольдса при течении в трубе соответствуют определенные границы относительной шероховатости, в которых можно пользоваться теми или другими формулами. В частности, для режима развитой шероховатости в рамках полуэмпирической теории с использованием логарифмического профиля скоростей можно получить закон сопротивления (формула Никурадзе):

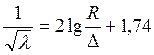, где R – радиус трубы, Δ – высота зерен шероховатости.

Наряду с приведенными формулами для определения коэффициента гидравлического сопротивления разными исследователями получены к настоящему времени иные полу- или эмпирические соотношения, в достаточной степени удовлетворяющие практике. Так, Альтшуль, рассматривая турбулентный поток в трубе как единое целое, т.е. не выделяя в нем ламинарный подслой, получил зависимость для закона сопротивления, справедливую для всех трех зон турбулентного режима:

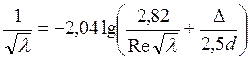
Однако, очевидно, что для практического использования эта формула неудобна, поскольку величина λ входит в неявном виде. Поэтому, используя некоторые допущения, Альтшуль предложил приближенную формулу, дающую достаточно точные результаты для всех трех турбулентных режимов:

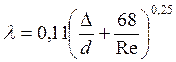
Если трубы достаточно гладкие и, следовательно, Δ/d << 68/Re, то эта формула практически совпадет с эмпирической формулой Блазиуса для гладкостенного режима течения: .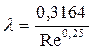

В случае полного (развитого) режима шероховатости, а это обычно соответствует достаточно большим значениям числа Рейнольдса, Δ/d >> 68/Re и формула Альтшуля переходит в эмпирическое соотношение Шифринсона:

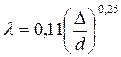для так называемой квадратичной зоны сопротивления.

Понятие средней высоты бугорков шероховатости Δ, которое мы использовали и которое фигурирует в приведенных формулах, недостаточно четко определено. Действительно, очевидно, что на распределение скоростей около стенки и, следовательно, на гидравлическое сопротивление влияет не только средняя высота выступов, но и их форма и распределение вдоль обтекаемой поверхности. Поэтому на практике пользуются эквивалентной шероховатостью, под которой понимают такую высоту песчинок в опытах Никурадзе, которая создает сопротивление, равное (или эквивалентное) сопротивлению данного действительного трубопровода.

В заключение приведем наиболее удобные для практического использования расчетные формулы для коэффициента гидравлического сопротивления (законы сопротивления) во всех рассмотренных режимах течения в круглой трубе.

Режим течения	Границы зоны	Расчетные формулы
Ламинарный	Re < 2300	λ = 64/Re
Турбулентный, гладкостенный	4·10^3< Re < 20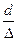
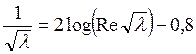
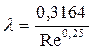
Турбулентный, промежуточный, с частичным проявлением шероховатости.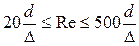
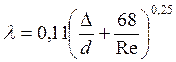
Турбулентный, развитая шероховатость, квадратичный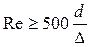

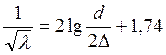
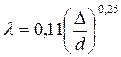
Для промышленных труб с неравномерной шероховатостью в формулы, приведенные в таблице, следует подставлять значения эквивалентной шероховатости, которые можно найти в гидравлических справочниках с учетом технологии изготовления труб, материала стенок, времени их эксплуатации.

СОДЕРЖАНИЕ

1. Одномерная модель течения вязкой несжимаемой жидкость

2. Уравнение Бернулли для потока вязкой несжимаемой жидкости

3. Режимы движения жидкости, их связь с гидравлическим сопротивлением

4. Ламинарное течение в круглых трубах

5. Основные особенности турбулентных течений

6. Уравнения Рейнольдса для осредненного турбулентного движения

7. Полуэмпирические соотношения в теории турбулентности

8. Турбулентное течение вблизи твердой стенки.

9. Потери давления (напора) при турбулентном течении в трубах

Дата добавления: 2014-01-05