Пример 1.8

Метод деления.

Деление на q (при помощи арифметики основания р). Если представление числа u по основанию q имеет вид (0,U_-1U_-2… U_-n), то можно, используя арифметику основания р, вычислить U_-1q^-1 + U_-2q^-2+… +U_-nq^-n в виде:

((…(U_-n/q+ U_-n+1)/q+…+ U_-2)/q+ U_-1)/q

Необходимо внимательно следить за ошибками, которые могут появиться в результате усечения или округления при делении на q; ошибки эти обычно пренебрежимы, но не всегда.

Преобразовать дробь (0,1011)₂ в десятичную систему счисления.

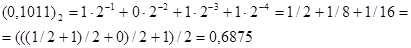
Метод умножения преобразования дробей используется при переходе из “родной” в “чужую” систему счисления, а метод деления – из “чужой” в “родную”.

1.2.3. Перевод чисел с основанием q=p^k.

Наиболее прост перевод чисел из q-ичной системы в p-ичную (или обратно), если имеет место соотношение q=p^k (k- целое положительное) и обе системы имеют неотрицательные базы.

В этом случае перевод из q–ичной системы счисления в p–ичную производят “поразрядно”, заменяя каждую q–ичную цифру равной ей k–разрядным числом, записанным в p–ичной системе счисления. Перевод из p–ичной системы в q–ичную производят при этом следующим образом. Двигая от запятой вправо и влево, разбивают p–ичную запись числа на группы по k цифр. Если при этом самая левая или самая правая группы окажутся неполными, к ним приписывают соответственно слева и справа столько нулей, чтобы каждая из них содержала k цифр. После этого каждую группу p–ичных цифр заменяют одной q–ичной цифрой, равной числу, обозначенному этой группой p–ичных цифр. Большой практический интерес представляет случай, когда p=2 (двоичное основание).

В этом случае имеем частный случай двоично-кодированной системы счисления, при которых двоичное число и двоично-кодированное число совпадают. Этот факт используют для более короткой записи двоичных чисел. Обычно берут p=2³=8 (восьмеричная система счисления) и p=2⁴=16 (шестнадцатеричная система счисления).

Дата добавления: 2014-01-05