Быстрое преобразование Фурье

Классическое, или «медленное» преобразование Фурье ВР из N отсчетов требует ~N² операций. Это ограничивает его использование в задачах RT. Для сокращения объемов вычислений разработаны алгоритмы БПФ, среди которых одним из самых распространенных является алгоритм Кули-Тьюки 1965.

Применение БПФ для ВР с количеством элементов N=2^p позволяет сократить объем вычислений с N² до 4N_p операций, т.е. в 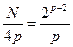раз. Т.к. 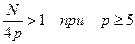, применение БПФ оправдано при N≥32.

Идея БПФ: вместо одного ПФ ВР из N элементов выполнить N*p БПФ ВР-в из 2 элементов. Рассмотрим схему БПФ ВР, состоящую из 8 элементов:

p
N
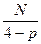
	1.6		25.6	83.3	157.5

N=8; p=3.

БПФ представляет собой оперативную процедуру из р шагов.

При l=1 ВР x_i iє (0,p-1) (0…7) разбивается пополам и вычисляются ПФ каждой пары членов ВР, отстоящих на N/2 (на 4: x₀±x₄; x₁±x₅; x₂±x₆; x₃±x₇).

При l=2 каждая половина ряда, состоящего из N преобразований А₁(i) снова делится пополам, и находятся преобразования каждой пары преобразованных переменных, расположенных в соседних четвертях: (А₁(0)± А₁(2); А₁(1)± А₁(3); А₁(4)± А₁(6); А₁(5)± А₁(7)).

При l=3 каждая четверть делится на 2*1/8 и находятся преобразования соседних членов, представляющих собой результаты предыдущего преобразования. (А₂(0)± А₂(1); А₂(2)± А₂(3); …).

Рассмотрим алгоритм БПФ. Представим номер элемента ВР (временной индекс) i и номер ординаты ПФ к (частотный индекс) в двоичном виде:

i=i_p-1*2^p-1+ i_p-2*2^p-2 +…+i₀*2⁰; (1)

k=k_p-1*2^p-1+ k_p-2*2^p-2 +…+k₀*2⁰; (2)

Коэффициенты i_j и k_j представляют собой биты и принимают значения 0 или 1. БПФ является оперативной процедурой из р шагов, на каждом шаге которой вычисляется вектор преобразованных переменных А_l размерностью N: A_l=f(A_l-1), l є [1,p]. В качестве А_l-1/l=1=A₀=x_i=x(i_p-1,…,i₀), а конечное становится равным искомому ПФ: x_k=x(jkΔω)=A_p(k_p-1;k_p-2,… k₀), где - нормированная частота (по сути).

Для получения каждого последующего вектора переменных А_l старшие временные индексы i_p-1,i_p-2,… в выражении для предыдущего вектора А_l-1 последовательно заменяются младшими частотными: k₀, k₁ и т.д. В результате получаем:

А₁= А₁(k₀, i_p-2,i_p-3,…i₀);

А₂= А₂(k₀,k₁, i_p-3,…i₀);

…

А_l= А₁(k₀,k₁,…k_l-1, i_p-l-1,…i₀);

…

А_p= А_p(k₀,k₁,…k_p-1)

Рекурсивные выражения для нахождения А_l имеют вид:

А₁(0, i_p-2, …, i₀)= А₀(0, i_p-2, …, i₀)+ А₀(1, i_p-2, …, i₀) (3)

k₀ i_p-1 i_p-1

А₁(1, i_p-1, …, i₀)= А₀(0, i_p-2, …, i₀)+ А₀(1, i_p-2, …, i₀) (4)

k₀ i_p-1 i_p-1

A_l(k₀,k₁,…,k_l-2,0, i_p-l-1,…, i₀) = A_l-1(k₀,k₁,…,k_l-2,0, i_p-l-1,…, i₀) +

k_l-1 i_p-l

+A_l-1(k₀,k₁,…,k_l-2, 1, i_p-l-1,…, i₀) (5)

i_p-l

A_l(k₀,k₁,…,k_l-2,1, i_p-l-1,…, i₀) = A_l-1(k₀,k₁,…,k_l-2,0, i_p-l-1,…, i₀) -

k_l-1 i_p-l

-A_l-1(k₀,k₁,…,k_l-2, 1, i_p-l-1,…, i₀),l=2…p (6)

i_p-l

Получаемый по выражениям (5) (6) вектор А_р содержит обратный порядок следования битов (на месте старшего – младший бит и наоборот), поэтому следует переупорядочить биты, изменив номера элементов А_р(). При этом крайние элементы А_р(0) и А_р(N-1) не изменят своих номеров.

Пример: ВР из 4 элементов: N=4, p=2 /*экономически не оправдано */. Классическое ПФ по формуле: 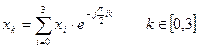(7)

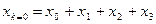
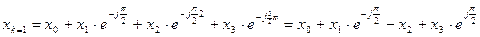
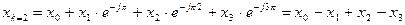
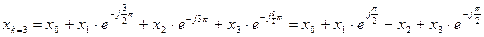
Найдем теперь БПФ по формулам (3)-(6).

А₁(0, i₀)=A₀(0, i₀)+A₀(1, i₀); А₁(1, i₀)=A₀(0, i₀)-A₀(1, i₀)

k₀ i₁ i₁ k₀ i₀ i₁

A₁(0)=x₀+x₂; A₁(1)=x₁+x₃; A₁(2)=x₀-x₂; A₁(3)=x₁- x₃

k₀ =0,i₀=0 k₀ =0,i₀=1 k₀ =1,i₀=0 k₀ =1,i₀=1

k₁ i₀ i₀ биты

k₁ i₀ i₀ биты

Т.о.:

А₂(0)=А₁(0)+А₁(1)=(х₀+х₂)+(х₁+х₃) (к₀=0, к₁=0)

А₂(2)=А₁(2)+А₁(3)*e^-jπ/2=х₀+х₁e^-jπ/2-х₂+х₃e^jπ/2 (к₀=1, к₁=0)

А₂(1)=А₁(0)-А₁(1)= х₀-х₁+х₂-х₃ (к₀=0, к₁=1)

А₂(3)=А₁(2)-А₁(3)*e^-jπ/2=х₀+х₁e^jπ/2-х₂+х₃e^-jπ/2 (к₀=1, к₁=1)

Заменив порядок следования битов, получим:

А₂(2)→А₂(1); А₂(1)→ А₂(2).

Результаты МПФ и БПФ совпадают.

Спектральный анализ временных рядов.

Дата добавления: 2014-01-05