Режекторный фильтр(заграждающий)

ФВЧ.

ФНЧ.

Типы фильтров.

Идеальный:B=f₀(=f_x)

B-частота пропускания, f₀- частота среза

f₀

АЧХ реальных фильтров имеют отклонение от номинальных значений, максимальные значение этих отклонений задаются на стадии проектирования и указываются на диаграмме требований.

1+δ₁

1 f_x 2 f_k δ₂ 3 f_g/2

f_x - частота среза;

f_k - граничная частота;

δ₁ – максимальное допустимое отклонение АЧХ от 1;

δ₂ – максимальное допустимое отклонение АЧХ от 0;

1 – полоса пропускания;

2 – переходная полоса;

3 – полоса задерживания;

a_max = 20lg(1- δ₁) – максимальное допустимое ослабление в полосе пропускания.

a₀ = 20lg δ₂ < 0 – максимальное допустимое ослабление в полосе задерживания.

Синтез сводится к выбору управления и определению параметров.

Качество фильтра тем лучше, чем выше порядок уравнения.

f₀ f₁

f₀- частота среза, f₁-некоторая большая частота, для ЦФ f₁=f_k/2=1/2T_k

3.Полосно-пропускной фильтр.

f₀ f₀ – середина полосы пропускания

В

имеет характеристику, обратную ППФ

f₀

Явление транспонирования частот.

Это явление заключается в том, что при дискретизации сигнала (по времени) возникает НЧ-составляющая, проходящая через систему. Причиной тому:

1. Выбор параметров дискретизации исходя из параметров полезного сигнала: f_g≥2f_Bs.
2. Наличие в полном сигнале помимо полезного - шумового ВЧ-компонента.

В результате наблюдается преобразование ВЧ-гармоник шума в НЧ, называемое транспонированием (подменой) частот.

T_g

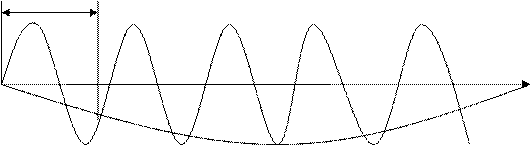
Если ВЧ-гармоника w_ВЧ=2π/T_ВЧ, дискретизируется с частотой w_g=2π/T_g, причём

w_g/2 < w_ВЧ < w_g1

то есть 2T_g>T_N>T_g, в результате возникает НЧ-гармоника той же амплитуды (рис.), но гораздо меньшей частоты:

w_НЧ=w_g-w_ВЧ

T_НЧ=2π/ w_НЧ = T_gT_ВЧ / (T_ВЧ - T_g)

Транспонирование частот при дискретизации сигналов требует подавления ВЧ-шумов в диапазоне w_g/2 … w_g. Для этого применяют противоподменный фильтр. На входе АЦП (см. л. 1-2, типовые схемы), п.с. ФНЧ с В= w_g/2.

Аналоговые и цифровые фильтры описываются ДУ и КРУ соответственно.

Улучшение характеристик достигается повышением порядка уравнения, отсюда следует усложнение схемы или алгоритма фильтра.

Вообще, под линейной цифровой фильтрацией понимают любое линейное преобразование сигнала, выполняемое в цифровой форме. В ОС типах преобразование можно записать:

	∞

y_k= ∑ c_i x_k-i (1)

i=-∞

Выделяют 2 обширных класса фильтров:

1.КИХ – фильтры (нерепурсивные, трансверсиальные). Выход зависит только от входа и конечного числа коэффициентов фильтра.

	N

y_n= ∑ c_k x_n-k

	i=1

N

N

2.БИХ-фильтры (репурсивные).Выход зависит от предыдущего значения выхода

y_k= ∑ b_ix_n-i - ∑ a_iy_n-1 (2)

	i=0		i=1

БИХ-фильтры проще реализовать. Основной метод их расчёта – аппроксимация известных аналоговых фильтров.

трансверсиальные – по структуре

x_n x_{n-1 …………}

Дата добавления: 2014-01-05