Фильтры первого порядка

ЦФ 1 описывается конечно-разностным уравнением первого порядка вида:

	n-1

i=0

y_k+a₁y_k-1= ∑ b_ix_k-i (3)

n-1

или

y_k= ∑ b_ix_k-i - a₁y_k-1 (4)

	i=0

где x_k-входной сигнал(фильтруемый ВР); y_k-выходной сигнал (оценка полезного сигнала).

Параметры фильтров первого порядка:

а) фильтр скользящего среднего:

	t

Analog: y(t)=1/T_ф ∫ x(τ)d τ (5) T_ф-

_t-Tф

------ память фильтра

	n-1

i=0

Digital: y_k=1/N ∑ x_k-I (6) N-

N определяет степень фильтрации

N = 1→ y_k=x_k (фильтрация отсутствует);

N = ∞→ y_k=const (среднее значение всего временного ряда).

Чтобы избавиться в (6) от ∑, перейдём к рекуррентной форме:

y_k=y_k-1+1/N(x_k-x_k-N) (7)

что позволяет экономить RAM.

Если допустить, что y_k-1= x_k-N,

то y_k=(1/N)x_k+(1-1/N)y_k-1 (8)

или y_k=αx_k+(1-α) y_k-1 ; α=1/N (9)

В этом случае требуется хранить только y_k-1.

б) Фильтр экспоненциального сглаживания:

Более разумно учитывать более свежие наблюдения с большим весом, что реализовано в ФЭС (через экспоненциальную систему весов).

	t

Analog: y(t) = 1/T_ф ∫ e^(-t-τ)/Tф x(τ)d τ (10)

	∞

Dig: Весовая функция:

e^{a t} = e^{a i T}= βⁱ (β=e^aT)

βⁱ определяется как геометрическая прогрессия: βⁱ = a_i = a₁*g_i с начальным членом a₁ = α и знаменателем g = (1-α).

Таким образом, наблюдения x_k-i берётся в ФЭС с весом γ_i = α (1-α)ⁱ, при этом сумма весов γ_i→ 1 при n→ ∞ (как следует из формулы для суммы ГП):

lim_{n→ ∞}S_n = a₁ / (1-g) = α / (1-(1- α)) =1

Уравнение дискретного ФЭС:

y_k= αx_k+ α(1- α)x_k-1+ α(1- α)²x_k-2+…+ α(1- α)ⁱx_k-i = α ∑ (1- α)ⁱx_k-I (11)

Запишем (11) в рекуррентной форме

y_k= αx_k+(1- α)y_k-1 (12)

Как видно, рекуррентная форма у ФЭС (9) и у ФЭС (12) совпадает, но коэффициенты различны (но здесь без всяких допущений).

Степень фильтрации ФЭС определяется значением α.

При α→0, y_k=y_k-1=const (полная фильтрация, оставляющая только const)

При α→1, y_k=x_k (фильтрация отсутствует)

На практике α=0,05…0,3

ФЭС и ФСС в форме (9) эквивалентны, если средний возраст наблюдений совпадает.

У ФСС:

τ_ср.=(n-1)/2 (13)

	∞

У ФЭС:

τ_ср=α ∑ i(1-α)ⁱ = (1-α)/α (14)

	i=0

Таким образом, ФСС и ФЭС эквивалентны, когда

(n-1)/2 = (1- α)/α или α=2/(n+1) (15)

ФЭС с α=0,1 эквивалентен ФСС с n=19.

Передаточная функция ФСС, соответствующая (7):

W(z)=y(z)/x(z)=(1/n)*(1-z^-n)/(1-z^-1) (16)

Заменив z на e^jwT и извлекая корень, получим АЧХ ФСС:

A(w)=1/n√(1-Cos(wnT))/(1-CoswT) (17)

ПФ и АЧХ ФЭС:

W(z)=α/(1-(1- α)z^-1) (18) A(w)= α/√1+(1- α)²-2(1- α)CoswT (19)

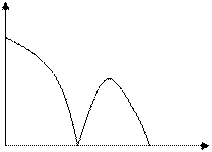
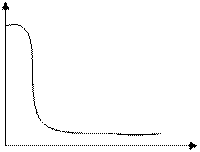
АЧХ ФСС ФЭС

Дата добавления: 2014-01-05