
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Спектры некоторых типовых сигналов
|
|
|
|
Понятие о спектре непериодического сигнала
Понятие о расчете цепей при периодических сигналах
Спектр последовательности прямоугольных импульсов
Графическое и частотное изображение спектра периодического сигнала
 графическое изображение
графическое изображение
 АЧС
АЧС
Аналогично ФЧС, только учитывая, что фазы могут быть отрицательными.
Такой спектр называется дискретным или линейчатым, он характерен для периодического сигнала.
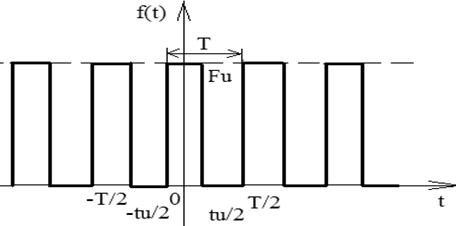
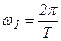
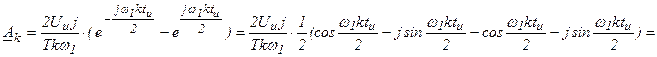
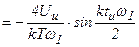
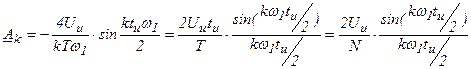 , где
, где 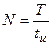 - скважность.
- скважность.
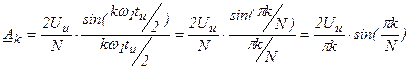
Найдем нулевые точки синуса:
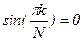
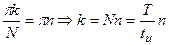
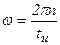
АЧС последовательности прямоугольных импульсов:
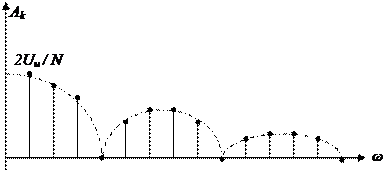
Первая нулевая точка – самая важная для спектра последовательности прямоугольных импульсов.
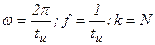
Основную долю энергии несут гармоники, расположенные от 0 до первой нулевой точки (около 90% энергии). Эту область частот, где сосредоточено 90% энергии сигнала, называют шириной спектра (частотного) сигнала.
Для прямоугольного импульса ширина спектра -  .
.
Любая цифровая передача сигнала требует большего спектра, чем простая аналоговая.
ФЧС последовательности прямоугольных импульсов:
Влияние длительности импульса и периода на вид спектра
Если длительность уменьшается, то основная частота не изменится, нулевые точки переместятся вправо. До первой нулевой точки, где сосредоточена основная энергия, попадает больше составляющих. Технически отмечают, что спектр расширяется.
Если же длительность импульса возрастает, то происходит сужение спектра.
Если период повторения увеличивается, то уменьшается основная частота. Если период повторения уменьшается, то основная частота увеличивается.
Изменение положения импульса или начала отсчета
Это не влияет на АЧС, при этом изменяется только фазовый спектр. Это можно отразить на основе теоремы запаздывания:

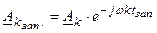
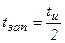
Фазовый спектр для первого сигнала N=4:

Методика расчета:
- Определяется комплексный спектр периодического сигнала;
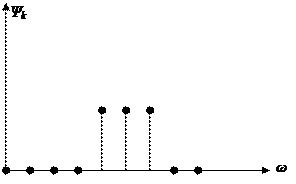
- Оценивается спектр, оставляют наиболее значащие гармоники (первый критерий: отсекаются все, который составляют менее 0,1 от максимальной гармоники);
- Рассчитываются токи и напряжения от каждой составляющей в отдельности. Можно использовать комплексный метод расчета.
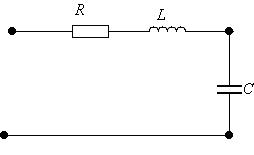
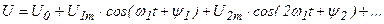
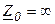
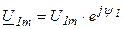
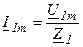
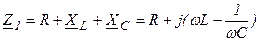
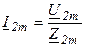

Оценить негармоническую функцию можно по негармоническому значению, т.е. среднеквадратичному за период:
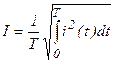
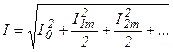
Непериодические сигналы являются самыми важными, так как именно они несут информацию. Периодические сигналы являются служебными для передачи информации, а новой информации не несут. Поэтому возникает вопрос спектров непериодических сигналов. Их можно попробовать получить предельным переходом из периодических сигналов, устремив период к бесконечности (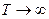 ). Остается одиночный сигнал. Найдем комплексную амплитуду одиночного сигнала:
). Остается одиночный сигнал. Найдем комплексную амплитуду одиночного сигнала: 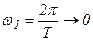 .
.
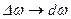 ,
,
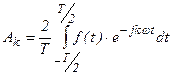
Непериодический сигнал можно разбить на бесконечную сумму гармонических составляющих с бесконечно малыми амплитудами и отличающихся по частоте на бесконечно малые величины – называется сплошным спектром, а не дискретным. Для расчетов используют понятие не комплексных амплитуд, и спектральной плотности амплитуд - величины амплитуды, приходящейся на единицу частоты.
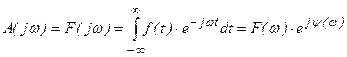
Здесь F(ω) – спектральная плотность амплитуд, ψ(ω) – спектр фаз.
Размерность плотности амплитуд отличается от размерности исходного сигнала. Спектр непериодического сигнала похож на спектр такого же по форме периодического сигнала, но является сплошной непрерывной функцией частоты.
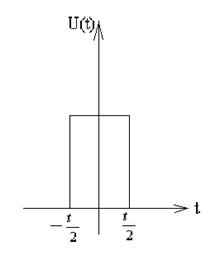 Найдем спектральную плотность одиночного прямоугольного импульса при симметричном распределении.
Найдем спектральную плотность одиночного прямоугольного импульса при симметричном распределении.
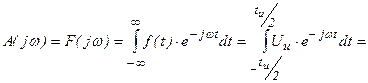
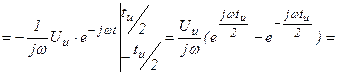
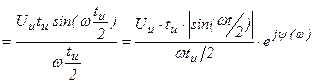
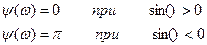
Получается непрерывная функция частоты вида 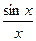
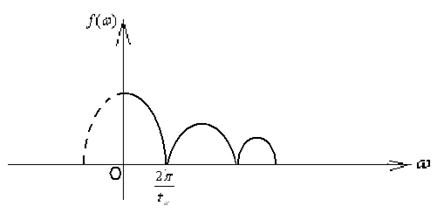
Вывод: Спектр одиночного сигнала похож на спектр последовательности таких же сигналов, точнее соответствует огибающей спектра дискретного сигнала, но размерности у них разные.
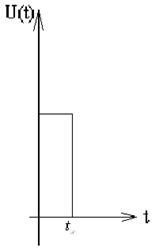 Рассмотрим несимметричное расположение сигнала.
Рассмотрим несимметричное расположение сигнала.
Найдем его спектр. Это можно сделать напрямую с помощью интеграла Фурье, а можно по теореме запаздывания.

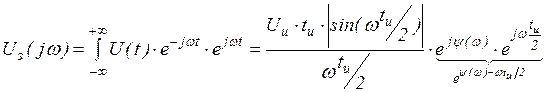
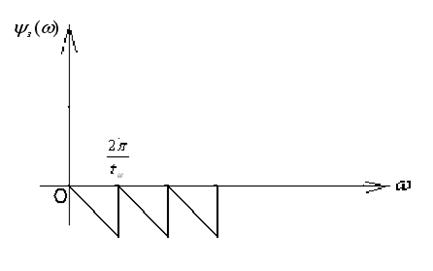
Спектральная плотность амплитуд не изменяется, спектр фаз показан ниже.
Их можно получить на основе прямого преобразования Фурье, а можно из операторных изображений этих сигналов, заменив p на jω.
1) Единичная ступенчатая функция: 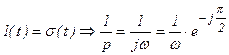 . Следовательно, спектральная плотность равна
. Следовательно, спектральная плотность равна 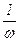 .
.
2) Единичная импульсная функция 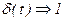 . Спектральная плотность равна 1, т.е. спектральная плотность равномерна.
. Спектральная плотность равна 1, т.е. спектральная плотность равномерна.
3) Экспонента: 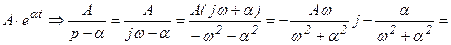
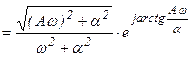
4) Профессиональный – радиоимпульс
Радиоимпульс ─ сигнал, огибающая которого соответствует прямоугольному импульсу, но он имеет заполнение какой-то частотой.
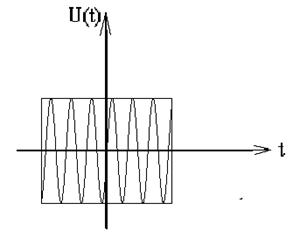
Частота заполнения ─ технически частота несущей радиостанции.
Определим спектр такого сигнала. Это можно сделать, используя теорему смещения в области комплексного переменного.
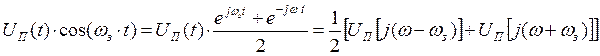
Импульс переносится в район частоты 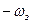 и
и 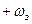 .
.

На этом принципе работают все радиостанции, передающие радиосигналы.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 6166; Нарушение авторских прав?; Мы поможем в написании вашей работы!