Многоканальные пуассоновские СМО

<le^-lt, me^-mt, m>1, N>

6.1. СМО без очереди (N=0)

S0

S1

...

Sm

Рис. 7. Размеченный граф СМО.

Составим систему уравнений для определения вероятностей состояний

P₁=P₀l/m=rP₀, где r=l/m

P₂=P₁×r/2=P₀×r²/2

P₃=P₂×r/3=P₀

Вероятность состояний S_k равны

P_k=P₀ k=1,...,m

Вероятность Р₀ определяется из условия

Вероятность отказа в обслуживании равна:

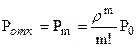
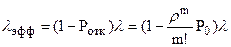
Т.к. очередь отсутствует среднее время нахождения заявок в СМО равно

Среднее число заявок в СМО равно

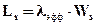
6.2. СМО с ограниченной очередью (N>0)

l l l l l l

S1

S2

S3

¼

Sm

¼

SN+m

m 2m 3m mm mm mm

Рис. 8 Размеченный граф СМО.

Составим систему уравнений для определения вероятностей состояний

P₁=P₀l/m=rP₀, где r=l/m

P₂=P₁×r/2=P₀×r²/2

P₃=P₂×r/3=P₀

P_k=P₀ k=1,...,m

Введем обозначение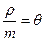

учитывая условие, что сумма всех вероятностей равна единице.

, получим P₀:

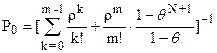(14)

Определим среднее число заявок в очереди: ,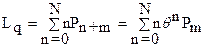

где .

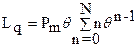(15)

Введем в рассмотрение функцию:

(16)

Подставим (16) в (15), получим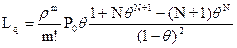

Вероятность отказа в обслуживании равна:

Эффективный поток заявок: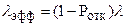

Используя формулы Литтла, получим среднее время ожидания заявок в очереди:

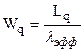
Время в СМО отличается от W_q на время обслуживания: .

Наконец среднее число заявок в системе равно: .

Частный случай

Рассмотрим случай, когда .

Система уравнений для определения Р_n примет вид:

.

Определим Р₀

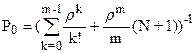
Средняя длина очереди равна: ,

учитывая, что получим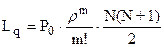

Пример расчета характеристик многоканальной СМО с ограниченнной очередью.

В мастерской шиномонтажа работают 2 мастера (m =2), которые обслуживают клиентов с интенсивностью 2 авто в час. Поток клиентов 4 в час. Максимальное число мест для ожидания 4 (N=4).

Решение.

ρ= λ/ μ = 4/2 = 2; θ= ρ/ m = 1.

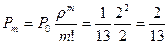
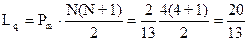запросов,

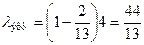
W_q= час.

W_s= час.,

L_s =l_эфф×W_s= 4 × 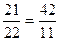запросов.

Дата добавления: 2014-01-05