Ациклические сети СМО

В ациклических сетях каждая заявка может посетить узел не более одного раза. Это условие означает, что в сети отсутствуют циклы, а матрица вероятностей переходов имеет следующий вид:

:

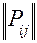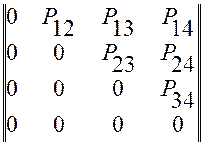
Рассчитаем величины входных потоков на каждый узел (нагрузку на узел).

Характеристики каждого узла 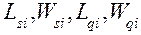рассчитываются как для одноканальной СМО:

; ; ;

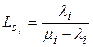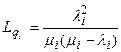
Характеристики всей сети СМО определяются следующим образом:

.

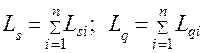Среднее время нахождения заявки в сети:

где вероятность посещения заявки СМО_i

Среднее время ожидания заявки во всех узлах сети: .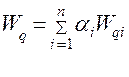

7.3. Циклические сети СМО.

В циклических сетях заявка может посетить один узел неоднократно. Пример такой сети приведен ниже.

Для анализа циклических сетей совместим “выход” и “источник”. Матрица вероятностей переходов для циклических сетей произвольная.

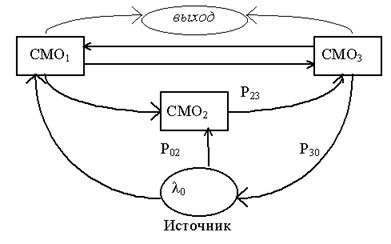
Рассматривая процесс перехода заявки от узла к узлу как марковский процесс, рассчитаем предельные вероятности нахождения заявки в каждом узле. Для этого решим следующее векторное уравнение (см. п. 4.1).

Отношение 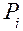к 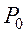следует интерпретировать как частоту посещения заявки i узла (СМО_i)., вышедшей из источника.

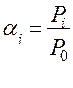
Тогда входной поток в узел i будет определяться по формуле:

Зная интенсивность обслуживания в каждом узле 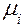, рассчитаем характеристики по каждому узлу .

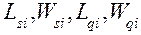Расчет характеристик сети в целом ведется также, как и в ациклических сетях.

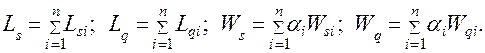
Пример расчета характеристик циклической сети СМО

Задана матрица переходов :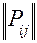

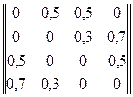
Входной поток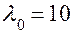

и интенсивности обслуживания заявок в узлах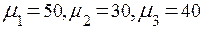

Находим предельные вероятности, решая систему уравнений:

Далее рассчитываем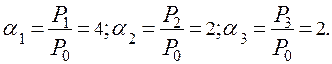

Входные потоки заявок на каждый узел будут равны:

Рассчитаем характеристики СМО в каждом узле:

;

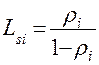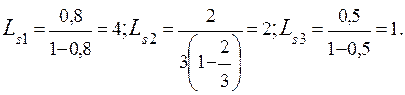
Интегральные характеристики по сети будут равны:

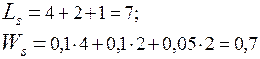
Дата добавления: 2014-01-05