Решение. 1. Рассмотрим равновесие точки А (или узла А), в которой сходятся все стержни и нити

1. Рассмотрим равновесие точки А (или узла А), в которой сходятся все стержни и нити.

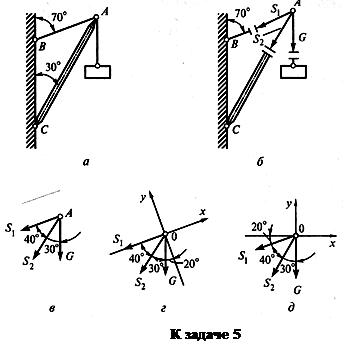
2. Активной силой является вес груза G, направленный вниз (рис. б).

3. Отбросим связи: стержень и нить. Усилие в нити обозна­чим Sx и направим от точки А, так как нить может испытывать только растяжение. Усилие в стержне обозначим S₂ и тоже на­правим от точки А, предполагая что стержень АС растянут (рис. б).

Выполним на отдельном чертеже схему действия сил в точке А (рис. в).

4. Выберем положение системы координат. Начало коорди­нат совмещаем с точкой А (рис. г). Ось х совмещаем с лини­ей действия усилия S, а ось у располагаем перпендикулярно оси х. Укажем углы между осями координат и усилиями S₁. и S₂.

5. Составим уравнения равновесия.

Из второго уравнения находим

Из первого уравнения находим

Знак «минус» перед S₂ свидетельствует о том, что стержень АС не растянут, как предполагалось, а сжат.

6. Проверку решения предлагаем выполнить самостоятельно, расположив оси координат так, как показано на рис. д.

Ответ: S₁ = 15,56 кН, S₂ = - 29,24 кН (при принятом на черте­же направлении усилий).

Величина усилий зависит от углов наклона стержня и нити. Например, если на рис. а угол 70° заменить на 60°, сохранив угол 30°, то усилия будут равны: S₁ = 20 кН, S₂ = - 34,64 кН. А при угле 50° S₁ = 29,26 кН, S₂ = - 44,8 кН. Оба усилия растут и становятся больше веса груза.

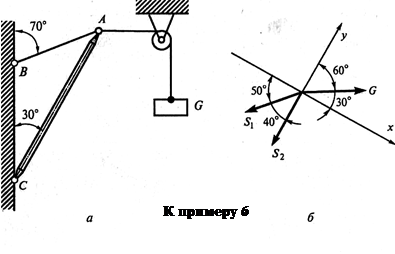
Пример 6. Как изменятся усилия в стержне и нити, если груз будет перекинут через блок, как показано на рис. а?

Остальные данные — в примере 5.

Решение

1. Рассматриваемой тонкой остается точка А.

2. Активная сила (вес груза G) действует на точку горизонтально слева направо, так как груз перекинут через блок.

3. Усилия S₁ и S₂ прикладываем к точке А, как в примере 2.

4. Выбираем систему координат, как показано на рис. б.

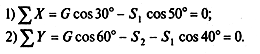5. Составляем и решаем уравнения равновесия:

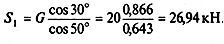Из первого уравнения находим

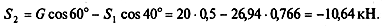Из второго уравнения находим

Ответ: S₁ = 26,94 кН; S₂ = - 10,64 кН при принятом направлении усилий на чертеже. Усилие S₁ увеличилось, S₂ — уменьшилось, а знаки не изменились.

Пример 7. Определить усилия в стержнях (рис. а). Массой стержней пренебречь.

Дата добавления: 2014-01-05