
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неинерциальные системы отсчета
|
|
|
|
Неинерциальной системой отсчета (НИСО) называется система, движущаяся ускоренно относительно
инерциальной системы отсчета (ИСО).
Наша задача состоит в том, чтобы найти уравнения движения в НИСО. Поскольку законы движения в инерциальных системах отсчета нам известны, то она сводится к установлению законов преобразования сил и ускорений при переходе от ИСО к НИСО.
В этом разделе мы ограничимся рассмотрением движений, происходящих с малыми скоростями ( ), т.е. останемся в рамках классической механики. Такой подход обусловлен двумя причинами. Во-первых, для задач, которые нам предстоит решать, достаточно формализма классической физики, во-вторых, поскольку математический аппарат релятивистской механики сложен, его использование может привести к неоправданным трудностям в понимании изучаемых физических процессов.
), т.е. останемся в рамках классической механики. Такой подход обусловлен двумя причинами. Во-первых, для задач, которые нам предстоит решать, достаточно формализма классической физики, во-вторых, поскольку математический аппарат релятивистской механики сложен, его использование может привести к неоправданным трудностям в понимании изучаемых физических процессов.
Напомним, что в классической механике длина масштабов и время считаются абсолютными, т.е. во всех системах отсчета время течет одинаково и одинаковы любые выбранные масштабы.
Итак, пусть имеются две произвольные системы отсчета 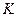 и
и  , движущиеся известным образом относительно друг друга. Заданы скорость
, движущиеся известным образом относительно друг друга. Заданы скорость 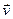 и ускорение
и ускорение  некоторой точки
некоторой точки  в
в 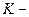 системе. Требуется найти соответствующие значения
системе. Требуется найти соответствующие значения  и
и 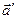 в
в  системе.
системе.
Договоримся произвольно выбранную ИСО, например 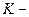 систему, считать неподвижной, а движение относительно неё условно назовём абсолютным. Движение системы отсчета
систему, считать неподвижной, а движение относительно неё условно назовём абсолютным. Движение системы отсчета  относительно
относительно 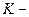 системы будем называть переносным. Движение тела относительно подвижной
системы будем называть переносным. Движение тела относительно подвижной  системы назовем относительным.
системы назовем относительным.
Тогда абсолютное движение тела складывается из его относительного движения и переносного вместе с подвижной системой отсчета.
Наша цель – изучить относительное движение.
Если движущаяся  система отсчета инерциальна, то законы движения – это законы Ньютона. Поэтому рассмотрим только те случаи, когда
система отсчета инерциальна, то законы движения – это законы Ньютона. Поэтому рассмотрим только те случаи, когда  система движется относительно неподвижной
система движется относительно неподвижной 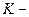 системы с ускорением.
системы с ускорением.
1.  система движется поступательно по отношению к
система движется поступательно по отношению к 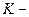 системе.
системе.
Пусть в 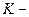 системе начало отсчета
системе начало отсчета  системы характеризуется радиус-вектором
системы характеризуется радиус-вектором  , а её скорость и ускорение – векторами
, а её скорость и ускорение – векторами  и
и  . Если положение точки
. Если положение точки  в
в 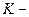 системе определяется радиус-вектором
системе определяется радиус-вектором  , а в
, а в  системе – радиус-вектором
системе – радиус-вектором  , то ясно, что
, то ясно, что  .
.
 Пусть далее за промежуток времени
Пусть далее за промежуток времени 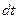 точка
точка 
совершит в 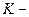 системе элементарное перемещение
системе элементарное перемещение 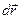 .
.
Это перемещение складывается из перемещения  вместе
вместе
с  системой и перемещения
системой и перемещения  относительно
относительно
 системы, т.е.
системы, т.е.
 . (1)
. (1)
Поделив это выражение на 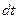 , получим искомую формулу
, получим искомую формулу
преобразования скорости:
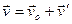 . (2)
. (2)
Продифференцировав полученное выражение по времени, найдем и формулу преобразования ускорения:
 . (3)
. (3)
2.  система вращается с угловой скоростью
система вращается с угловой скоростью  вокруг оси, неподвижной в
вокруг оси, неподвижной в 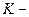 системе.
системе.
 Получим сначала преобразования при условии
Получим сначала преобразования при условии 
 .
.
Выберем начала отсчета 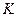 и
и  систем в произвольной точке
систем в произвольной точке 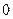
на оси вращения. Тогда в обеих системах отсчета радиус-вектор точки
 будет один и тот же:
будет один и тот же: 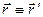 .
.
Если точка  неподвижна в
неподвижна в  системе (
системе ( ), это значит, что
), это значит, что
её перемещение 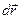 в
в 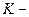 системе за время
системе за время 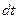 обусловлено только
обусловлено только
поворотом радиус-вектора  на угол
на угол 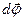 вместе с
вместе с  системой
системой
и равно векторному произведению  .
.
Если точка  движется относительно
движется относительно  системы со скоростью
системы со скоростью  ,
,
то за время 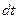 она совершит дополнительное перемещение
она совершит дополнительное перемещение  и тогда
и тогда
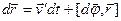 . (4)
. (4)
Поделив на 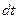 , получим формулу преобразования скорости:
, получим формулу преобразования скорости:
 , (5)
, (5)
где 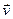 и
и  - скорости точки
- скорости точки  в
в 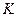 и
и  системах соответственно.
системах соответственно.
Перейдем к ускорениям.
В соответствии с (5) в 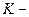 системе приращение
системе приращение 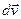 вектора
вектора 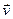 за время
за время 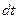 должно складываться из суммы приращений векторов
должно складываться из суммы приращений векторов  и [
и [ , т.е.
, т.е.
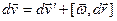 , т.к.
, т.к. 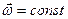 . (6)
. (6)
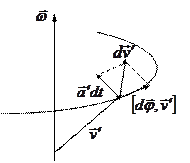 Если точка
Если точка  движется в
движется в  системе с постоянной скоростью
системе с постоянной скоростью
(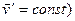 , то в
, то в 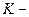 системе это приращение обусловлено
системе это приращение обусловлено
только поворотом вектора  вместе с
вместе с  системой и равно
системой и равно
 .
.
Если же точка имеет ускорение 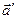 в
в  системе, то за время
системе, то за время
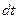 вектор
вектор  дополнительно получит приращение
дополнительно получит приращение 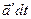 . Тогда
. Тогда
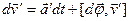 . (7)
. (7)
Подставив (4) и (7) в (6) и разделив на 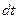 , получим формулу
, получим формулу
преобразования ускорения:
 , (8)
, (8)
где  и
и 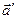 - ускорения точки
- ускорения точки  в
в 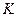 и
и  системах отсчета. Второе слагаемое носит название кориолисова (или поворотного) ускорения
системах отсчета. Второе слагаемое носит название кориолисова (или поворотного) ускорения
 , (9)
, (9)
третье слагаемое –осестремительное ускорение
 (10)
(10)
{не путать с нормальным (центростремительным) ускорением}.
Рассмотрим более общий случай, объединяющий два предыдущих.
3.  система вращается с угловой скоростью
система вращается с угловой скоростью  вокруг оси, перемещающейся поступательно со скоростью
вокруг оси, перемещающейся поступательно со скоростью  и ускорением
и ускорением  по отношению к
по отношению к 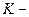 системе.
системе.
Легко понять, что формула преобразования скоростей примет следующий вид
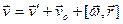 . (11)
. (11)
Формула преобразования ускорения в самом общем случае ( ) приобретет вид:
) приобретет вид:
 , (12)
, (12)
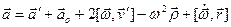 , (13)
, (13)
где  - радиус-вектор, перпендикулярный оси вращения и характеризующий положение точки
- радиус-вектор, перпендикулярный оси вращения и характеризующий положение точки  относительно этой оси.
относительно этой оси.
Введя обозначения  , объединив члены выражения (12), не зависящие от относительного движения точки
, объединив члены выражения (12), не зависящие от относительного движения точки  , можно написать
, можно написать
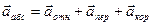 , (
, ( ). (14)
). (14)
Полученное выражение представляет собой математическую запись теоремы Кориолиса:
Абсолютное ускорение является векторной суммой относительного, кориолисова и переносного ускорений.
Основное уравнение динамики в НИСО.
Из выражения (13) следует, что ускорение частицы в  системе (здесь
системе (здесь 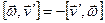 )
)
 . (15)
. (15)
Умножив обе части уравнения (14) на массу  частицы и учтя, что в ИСО
частицы и учтя, что в ИСО 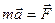 , получаем
, получаем
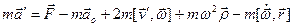 . (16)
. (16)
Это и есть основное уравнение динамики в неинерциальной системе отсчета, которая вращается с некоторой угловой скоростью  вокруг оси, перемещающейся поступательно с ускорением
вокруг оси, перемещающейся поступательно с ускорением  .
.
Очевидно, что даже при  частица будет двигаться в этой системе отсчета с ускорением, в общем случае отличным от нуля, причем так, как если бы на него действовали силы, описываемые членами уравнения (16). Эти силы получили название сил инерции.
частица будет двигаться в этой системе отсчета с ускорением, в общем случае отличным от нуля, причем так, как если бы на него действовали силы, описываемые членами уравнения (16). Эти силы получили название сил инерции.
Из вида уравнения (16) следует, что введение сил инерции позволяет сохранить форму записи основного уравнения динамики и для НИСО. Однако кроме силы 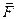 , обусловленной действием на частицу окружающих тел, необходимо учесть и силы инерции, описываемые остальными слагаемыми в правой части уравнения (16).
, обусловленной действием на частицу окружающих тел, необходимо учесть и силы инерции, описываемые остальными слагаемыми в правой части уравнения (16).
Силы инерции.
Перепишем основное уравнение динамики в НИСО (16) в виде:
 , (17) где
, (17) где
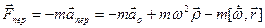 - переносная сила инерции. (18)
- переносная сила инерции. (18)
 (18а)
(18а)
часто называют поступательной силой инерции. Она, например, проявляется при резком торможении автомобиля, когда нас резко бросает вперед, т.е. в сторону, противоположную ускорению 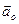 .
.
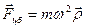 - центробежная сила инерции. (18б)
- центробежная сила инерции. (18б)
Примером проявления этой силы служат перегрузки, возникающие при поворотах.
Последний член в выражении (18) не имеет «специального» названия и «отвечает» за неравномерность вращения.
Важно отметить, что силы, входящие в выражение (18), как и, естественно, сама переносная сила, не зависят от относительной скорости  движения частицы, а являются исключительно следствием ускоренного движения НИСО.
движения частицы, а являются исключительно следствием ускоренного движения НИСО.
Совершенно иначе обстоит дело с третьим слагаемым в правой части уравнения (17).
 - сила Кориолиса, (19)
- сила Кориолиса, (19)
или кориолисова сила инерции.
Кориолисова сила возникает только тогда, когда частица движется ( ) во вращающейся НИСО, т.е. в отличие от других сил инерции зависит от относительного движения частицы.
) во вращающейся НИСО, т.е. в отличие от других сил инерции зависит от относительного движения частицы.
Итак, для описания движения частицы в НИСО кроме сил, обусловленных взаимодействием тел, мы формально ввели силы инерции. Каков же характер этих сил?
Они не являются силами в ньютоновском смысле, т.е. мерой взаимодействия тел, а обусловлены свойствами самих НИСО. Поэтому на силы инерции третий закон Ньютона не распространяется.
Силы инерции не инвариантны относительно перехода из одной системы отсчета в другую. И, наконец, они существуют только в НИСО. В ИСО этих сил нет – об этом необходимо помнить во избежание недоразумений.
Силы инерции всегда являются внешними по отношению к любой системе движущихся тел. Т.е. движение тел под действием сил инерции аналогично движению во внешних полях. Поэтому на силы инерции можно смотреть как на действие со стороны каких-то реальных полей.
Переносные силы инерции, так же как и ньютоновские, совершают работу.
Кориолисова сила инерции, как это следует из (19), всегда перпендикулярна скорости относительного движения тела ( ) и поэтому работы не совершает.
) и поэтому работы не совершает.
 гироскопическая сила, непотенциальная.
гироскопическая сила, непотенциальная.
Все силы инерции, подобно силам тяготения, пропорциональны массе тела.
Поэтому в однородном поле сил инерции, как и в поле сил тяготения, все тела движутся с одним и тем же ускорением независимо от их масс. Это весьма существенный факт с далеко идущими последствиями.
Движение тел на Земле.
Используем основное уравнение динамики в НИСО (16) применительно к движению тел относительно Земли.
 (16/)
(16/)
Переобозначим для простоты записи  ;
;  , т.к. всё, что нас интересует, происходит в НИСО, связанной с Землей (
, т.к. всё, что нас интересует, происходит в НИСО, связанной с Землей ( система).
система).
Далее, преобразуем уравнение (16/) в соответствии со следующими договоренностями:
1. Пусть Земля вращается равномерно, т.е. 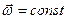 и
и  .
.
2. Выберем начало отсчета в центре Земли, тогда  и
и  – переносные скорость и ускорение центра Земли относительно неподвижной системы отсчета – Солнца (гелиоцентрическую систему отсчета называют также системой Коперника).
– переносные скорость и ускорение центра Земли относительно неподвижной системы отсчета – Солнца (гелиоцентрическую систему отсчета называют также системой Коперника).
3. Сила взаимодействия может быть представлена как  ,
,
где 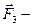 гравитационное притяжение Земли;
гравитационное притяжение Земли;
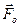 - равнодействующая гравитационного притяжения небесных тел – Солнца, Луны, звезд и других
- равнодействующая гравитационного притяжения небесных тел – Солнца, Луны, звезд и других
планет;
 - равнодействующая других сил (сопротивления воздуха, трения, упругости и т.д.)
- равнодействующая других сил (сопротивления воздуха, трения, упругости и т.д.)
В этих обозначениях уравнение (16/) приобретает вид
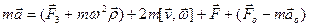 .
.
Обобщенный закон Галилея гласит: все тела в однородном поле тяготения падают с одинаковыми ускорениями.
Иначе говоря, сила, действующая на тело, строго пропорциональна массе тела. В этом отношении силы инерции, которые также строго пропорциональны массам тел, ведут себя так же, как и силы тяготения.
Посмотрим, как ведет себя поле тяготения вблизи поверхности Земли. Основной вклад в силу 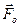 вносят гравитационные поля Солнца и Луны – небесных тел (НТ). Они убывают пропорционально обратным квадратам расстояний от этих тел (
вносят гравитационные поля Солнца и Луны – небесных тел (НТ). Они убывают пропорционально обратным квадратам расстояний от этих тел ( ) и поэтому неоднородны. Однако размеры Земли столь малы по сравнению с этими расстояниями, что, в первом приближении, изменениями внешних гравитационных полей на расстояниях порядка земного диаметра можно пренебречь, а сами поля считать однородными. Следовательно, в принятом приближении, внешнее гравитационное поле сообщает всем телам у поверхности Земли такое же ускорение, что и центру Земли, поэтому
) и поэтому неоднородны. Однако размеры Земли столь малы по сравнению с этими расстояниями, что, в первом приближении, изменениями внешних гравитационных полей на расстояниях порядка земного диаметра можно пренебречь, а сами поля считать однородными. Следовательно, в принятом приближении, внешнее гравитационное поле сообщает всем телам у поверхности Земли такое же ускорение, что и центру Земли, поэтому
 , или
, или 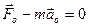 . (19/)
. (19/)
Т.о., силы гравитационного притяжения Солнца, Луны и других небесных тел в НИСО, связанной с Землей, полностью компенсируются поступательными силами инерции, возникающими из-за ускорения, сообщаемого Земле этими же гравитационными полями. Тогда
 . (20)
. (20)
Это уравнение движения тела вблизи поверхности Земли.
Векторная сумма  (сила взаимодействия
(сила взаимодействия  определяется из закона всемирного тяготения) пропорциональна массе тела и не зависит от скорости его относительного движения. Эта сумма характеризует только гравитационное поле Земли и её вращение.
определяется из закона всемирного тяготения) пропорциональна массе тела и не зависит от скорости его относительного движения. Эта сумма характеризует только гравитационное поле Земли и её вращение.
Представим её в виде:
 =
= 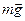 . (21)
. (21)
Определенная таким образом величина  одинакова для всех тел и определяется только лишь конкретной точкой пространства, а уравнение относительного движения тела принимает вид:
одинакова для всех тел и определяется только лишь конкретной точкой пространства, а уравнение относительного движения тела принимает вид:

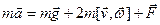 . (22)
. (22)
Чтобы установить физический смысл вектора  , положим скорость
, положим скорость 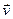 тела равной нулю и допустим, что внешних сил нет (
тела равной нулю и допустим, что внешних сил нет ( ). Тогда из (22) следует
). Тогда из (22) следует
 .
.
Т.о., вектор  есть ускорение свободно падающего тела относительно Земли при условии, что его скорость в рассматриваемый момент времени равна нулю.
есть ускорение свободно падающего тела относительно Земли при условии, что его скорость в рассматриваемый момент времени равна нулю.
Из (21) видно, что ускорение свободного падения является суммой двух слагаемых
 =
= 
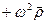 , (23)
, (23)
где  =
=  – ускорение, вызванное силой гравитационного притяжения Земли. Такое ускорение мы получили бы в неподвижной системе отсчета при условии, что, помимо земного гравитационного, никаких других полей нет.
– ускорение, вызванное силой гравитационного притяжения Земли. Такое ускорение мы получили бы в неподвижной системе отсчета при условии, что, помимо земного гравитационного, никаких других полей нет.
Второе слагаемое  – ускорение, сообщаемое центробежной силой инерции, связано с вращением Земли.
– ускорение, сообщаемое центробежной силой инерции, связано с вращением Земли.
Оговорка, сделанная выше по поводу относительной скорости, необходима, т.к. при 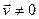 появляется дополнительное ускорение, обусловленное кориолисовой силой инерции.
появляется дополнительное ускорение, обусловленное кориолисовой силой инерции.
Вес тела.
Вес тела 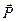 – это сила, с которой это тело действует на подставку (на которой оно лежит) или тянет за подвес (к которому оно подвешено).
– это сила, с которой это тело действует на подставку (на которой оно лежит) или тянет за подвес (к которому оно подвешено).
При этом тело и подставка (подвес) покоятся в системе отсчета, где производится взвешивание. Обычно, когда говорят о весе тела, предполагается, что тело и подвес (подставка), покоятся относительно Земли.
Если тело действует на подвес с силой 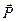 , то подвес действует на тело с противоположно направленной силой
, то подвес действует на тело с противоположно направленной силой  . По сути,
. По сути, 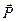 и
и  силы взаимодействия подвеса и тела. Поэтому они удовлетворяют третьему закону Ньютона:
силы взаимодействия подвеса и тела. Поэтому они удовлетворяют третьему закону Ньютона:  . Тогда, предполагая, что тело на подвесе покоится относительно Земли (
. Тогда, предполагая, что тело на подвесе покоится относительно Земли (
 ), из (22) получим
), из (22) получим
 , (24)
, (24)
Учитывая (23), можем записать
 , (25)
, (25)
т.е. вес равен геометрической сумме силы гравитационного притяжения Земли и центробежной силы инерции, а направление нити подвеса (отвеса) определяет направление силы 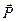 и, следовательно, ускорения свободного падения
и, следовательно, ускорения свободного падения  .
.
На рисунке показаны направления ускорений в предположении,
 что Земля имеет форму шара со сферически-симметричным
что Земля имеет форму шара со сферически-симметричным
распределением вещества по объему.
Вектор  направлен точно к центру Земли. Однако и в этом
направлен точно к центру Земли. Однако и в этом
случае направление отвеса не совпадает с вектором  , а
, а
определяется вектором  , т.е. диагональю параллелограмма,
, т.е. диагональю параллелограмма,
построенного на векторах  и
и  .
.
Для сферически симметричной Земли угол 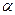 между
между
векторами ускорений можно найти с помощью теоремы синусов
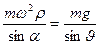 .
.
Учитывая, что 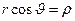 , получаем
, получаем
 , (26)
, (26)
где  - географическая широта места. На полюсе и на экваторе угол
- географическая широта места. На полюсе и на экваторе угол 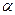 обращается в нуль.
обращается в нуль.
Для реальной Земли формула (26) приближенна, но достаточно точна.
Проектируя векторы  и
и  на направление вектора
на направление вектора  и полагая
и полагая 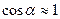 и
и  , получим приближенную (ошибка расчета порядка
, получим приближенную (ошибка расчета порядка  ) формулу, связывающую величину ускорения свободного падения с его компонентами
) формулу, связывающую величину ускорения свободного падения с его компонентами
 . (27)
. (27)
Опыты показали, что значения  и
и 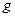 зависит от географической широты места.
зависит от географической широты места.
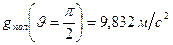 ;
;  ;
;
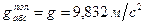 ;
; 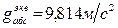 .
.
Если бы Земля была шаром со сферически-симметричным распределением вещества в нем, то величина 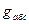 не должна была бы зависеть от широты места. Наблюдаемая разница объясняется сплюснутостью Земли, обусловленной действием центробежных сил.
не должна была бы зависеть от широты места. Наблюдаемая разница объясняется сплюснутостью Земли, обусловленной действием центробежных сил.
Совершенно аналогично «земной» складывается ситуация с определением веса тела на любом объекте, находящемся в поле тяготения небесных тел, например, на космическом корабле. В силу малых размеров корабля гравитационное поле, создаваемое небесными телами (Солнцем, Землей, Луной), с высокой степенью точности будет внутри корабля однородным. В корабле с выключенными двигателями, свободно падающем в гравитационном поле небесных тел, это поле полностью компенсируется поступательными силами инерции, возникающими в системе отсчета, связанной с кораблем, из-за ускорения, сообщаемого тем же самым гравитационным полем. Ввиду ничтожности гравитационного поля, создаваемого самим кораблем, в выражении (21) член 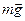 может быть обусловлен исключительно вращением корабля и равен
может быть обусловлен исключительно вращением корабля и равен  (центробежная сила). Если корабль не вращается (
(центробежная сила). Если корабль не вращается (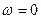 ), то
), то 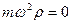 и вес любых тел, неподвижных относительно корабля, будет равен нулю, т.е. возникает состояние невесомости.
и вес любых тел, неподвижных относительно корабля, будет равен нулю, т.е. возникает состояние невесомости.
«Искусственная тяжесть» возникает при вращении корабля (нескомпенсированная внешними гравитационными полями центробежная сила) или при работе двигателей, сообщающих кораблю дополнительное поступательное ускорение (добавляется член 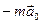 в уравнение (22)). Тогда все тела внутри космического корабля снова становятся «весомыми». Именно этим «весом» обусловлены перегрузки, которые испытывают космонавты при старте и торможении космических кораблей.
в уравнение (22)). Тогда все тела внутри космического корабля снова становятся «весомыми». Именно этим «весом» обусловлены перегрузки, которые испытывают космонавты при старте и торможении космических кораблей.
Однако приближение (19/) выполняется не всегда, и может нарушаться при определенном расположении Солнца и Луны. Следствием неоднородности внешних гравитационных полей (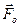 не строго равно
не строго равно  ) являются приливы.
) являются приливы.
Приливы.
У берегов океанов и морей дважды в сутки, с интервалом 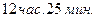 , наблюдается поднятие (прилив) воды до некоторого максимального уровня (полная вода), а затем её опускание (отлив) до минимального уровня (малая вода). Разность уровней большой и малой воды называется амплитудой прилива. Время между следующими друг за другом положениями полной (или малой) воды точно совпадает с половиной промежутка времени, в течение которого Луна в своем видимом движении совершает полный оборот вокруг Земли. Поэтому причину приливов и отливов уже давно связывали с положением Луны на небесном своде, но впервые объяснил это явление Ньютон.
, наблюдается поднятие (прилив) воды до некоторого максимального уровня (полная вода), а затем её опускание (отлив) до минимального уровня (малая вода). Разность уровней большой и малой воды называется амплитудой прилива. Время между следующими друг за другом положениями полной (или малой) воды точно совпадает с половиной промежутка времени, в течение которого Луна в своем видимом движении совершает полный оборот вокруг Земли. Поэтому причину приливов и отливов уже давно связывали с положением Луны на небесном своде, но впервые объяснил это явление Ньютон.
Возникновение приливов и отливов объясняется неоднородностью полей тяготения Луны и Солнца.
Очевидно, что гравитационное поле, создаваемое небесными телами, неоднородно. Поэтому в земной системе отсчета его полная компенсация поступательной силой инерции, связанной с ускоренным движением центра масс Земли, имеет место только в самом центре масс, куда мы помещаем начало отсчета. В остальных точках земного шара можно говорить лишь о приблизительном равенстве сил тяготения и обусловленной ими поступательной силы инерции. Нескомпенсированность именно этих сил наиболее существенно будет проявляться вблизи поверхности Земли, вызывая приливы. Хотя лунное поле тяготения слабее солнечного, но оно более неоднородно, поскольку Луна почти в 400 раз (384 тыс. км и 150 млн. км) ближе к Земле, чем Солнце, поэтому влияние Луны более существенно.
Следует отметить, что Луна обращается вокруг Земли по эллиптической орбите. В перигее она удалена от Земли на 57 земных радиусов, а в апогее – на 63,7 земных радиусов.
Если ввести приливообразующую силу 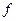 , обусловленную неполной компенсацией силы тяготения Луны (Солнца) поступательной силой инерции и отнесенную к единице массы, на которую они действуют, то для Луны отношение
, обусловленную неполной компенсацией силы тяготения Луны (Солнца) поступательной силой инерции и отнесенную к единице массы, на которую они действуют, то для Луны отношение  изменяется в пределах от
изменяется в пределах от 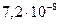 (в апогее) до
(в апогее) до  (в перигее). Для Солнца при его среднем удалении от Земли эта величина составляет
(в перигее). Для Солнца при его среднем удалении от Земли эта величина составляет 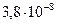 и меняется в течение года примерно на
и меняется в течение года примерно на 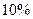 . Т.о., приливообразующая сила Луны в
. Т.о., приливообразующая сила Луны в  раза больше, чем Солнца.
раза больше, чем Солнца.
Очевидно, что приливообразующие силы ничтожно малы по сравнению с обычной силой тяжести на Земле. Если бы рассматриваемые силы оставались постоянными во времени, то они лишь слегка изменили бы равновесную форму свободной поверхности воды в океане. То обстоятельство, что эти силы вызывают такое грандиозное явление природы, как приливы и отливы, связано с тем, что они периодически меняются во времени. Это вызывает периодические изменения направления отвеса в каждой точке земного шара, что и является непосредственной причиной приливов и отливов.
Солнечные приливы накладываются на приливы лунные. При этом лунные приливы могут как усиливаться, так и ослабляться солнечными. В полнолуние и новолуние, когда Луна и Солнце находятся с одной стороны Земли, происходят большие (сизигийные) приливы. И наоборот, когда Луна находится в первой или последней четверти, наблюдаются малые (квадратурные) приливы.
Полная теория приливов ещё не создана. Это объясняется тем, что на характере приливов существенно сказывается большое число различных параметров: сложный рельеф дна океанов и морей, наличие материков и островов, очертания берегов, трение, морские течения и ветры, деформация самой Земли под действием приливообразующих сил и множество других трудно учитываемых факторов.
На открытых островах в океане амплитуда прилива в полнолуние и новолуние обычно достигает примерно одного метра. У берегов океана амплитуда приливов составляет около двух метров. Немного мест, где амплитуда приливов достигает трех метров, и очень мало, где шести. Все они находятся в узких проливах, либо в глубине длинных заливов. Наиболее значительные приливы наблюдаются в заливе Фунди, на восточном берегу Канады. Этот залив расположен между материком и полуостровом Новая Шотландия. Амплитуда прилива составляет  при входе в залив и нарастает до
при входе в залив и нарастает до 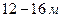 в глубине залива. Во время сизигийных приливов здесь наблюдались амплитуды свыше
в глубине залива. Во время сизигийных приливов здесь наблюдались амплитуды свыше 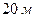 . (Сивухин, т.I. с. 360-366).
. (Сивухин, т.I. с. 360-366).
3.3. Отклонение падающих тел. Маятник Фуко.
Рассмотрим свободное падение тел в поле тяжести Земли. В этом случае мы должны положить  в уравнении (22), которое, с учетом вращения Земли, примет вид:
в уравнении (22), которое, с учетом вращения Земли, примет вид:
 (28)
(28)
Вращение Земли приводит к появлению центробежной силы, вклад которой учтен в векторе  , который теперь направлен не к центру Земли, а по отвесу (эта сила входит в вектор
, который теперь направлен не к центру Земли, а по отвесу (эта сила входит в вектор 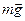 как его составная часть), и кориолисовой силы.
как его составная часть), и кориолисовой силы.
При падении тел без начальной скорости кориолисова сила инерции проявляется в отклонении свободно падающих тел к востоку и экватору от направления отвеса.
Точное решение этой задачи сводится к решению дифференциального уравнения (28) и, несмотря на его кажущуюся простоту, весьма громоздко и трудоемко. Более того, этот путь вряд ли оправдан, поскольку при самой формулировке уравнения (28) мы уже пренебрегли зависимостью  от координат.
от координат.
Здесь мы воспользуемся решением задачи, полученным методом последовательных приближений (см. Сивухин, т.I, с.354-356). Найденные этим методом выражения для восточного и экваториального отклонений имеют вид:
 ;
;  ,
,
где 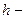 высота падания;
высота падания; 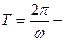 период суточного вращения земли;
период суточного вращения земли;  угол географической широты рассматриваемого места.
угол географической широты рассматриваемого места.
Из-за наличия малых множителей отклонения  и
и 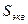 очень малы, причем
очень малы, причем 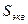 мало настолько, что недоступно экспериментальному измерению.
мало настолько, что недоступно экспериментальному измерению.
Значения  на широте Москвы (
на широте Москвы (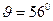 ) составляют
) составляют  при падении тела с высоты
при падении тела с высоты 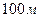 и
и 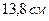 при
при 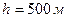 . Несмотря на малость эффекта, уже в середине XIX века его с уверенностью удалось наблюдать в опытах с падением тел в глубоких шахтах.
. Несмотря на малость эффекта, уже в середине XIX века его с уверенностью удалось наблюдать в опытах с падением тел в глубоких шахтах.
Опыты по отклонению падающих тел к востоку, в принципе, дают экспериментальное доказательство неинерциальности системы отсчета, связанной с Землей. Однако точность таких опытов, как мы видим, невелика, поэтому для этой цели больше подходит маятник Фуко.
Маятник Фуко.
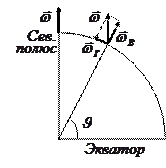 Маятник Фуко представляет собой массивный груз, подвешенной на длинной нити (проволоке), верхний конец которой укреплен с помощью карданного шарнира, позволяющего
Маятник Фуко представляет собой массивный груз, подвешенной на длинной нити (проволоке), верхний конец которой укреплен с помощью карданного шарнира, позволяющего
маятнику качаться в любой вертикальной плоскости.
Рассмотрим движение маятника Фуко в инерциальной системе отсчета,
связанной со звездами. Если маятник отклонить от вертикали и отпустить,
не сообщая ему начальной скорости, то действующие на груз маятника сила
земного тяготения и сила натяжения нити обеспечивали бы колебания в одной
плоскости, неподвижной в этой системе отсчета. В свою очередь, Земля,
совершая суточное вращение, поворачивалась бы относительно плоскости
качания маятника против часовой стрелки.
Наблюдатель, находящийся на Земле (в неинерциальной системе отсчета)
и вращающийся вместе с ней, видит, что плоскость качаний маятника Фуко
медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли. Этим опытом наглядно подтверждается факт суточного вращения Земли.
В неинерциальной системе отсчета, связанной с Землей, уравнение движения маятника имеет вид:
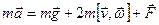 . (3.13)
. (3.13)
Поскольку сила 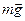 и сила натяжения нити
и сила натяжения нити  лежат в плоскости качаний маятника, то они не могут привести к её вращению. Поэтому, очевидно, вращение плоскости колебаний обусловлено действием кориолисовой силы инерции, причем скорость систематического вращения плоскости колебаний определяется лишь вертикальной (см. рисунок) составляющей
лежат в плоскости качаний маятника, то они не могут привести к её вращению. Поэтому, очевидно, вращение плоскости колебаний обусловлено действием кориолисовой силы инерции, причем скорость систематического вращения плоскости колебаний определяется лишь вертикальной (см. рисунок) составляющей  угловой скорости вращения Земли. Сила Кориолиса, обусловленная горизонтальной составляющей (см. рисунок) этой скорости
угловой скорости вращения Земли. Сила Кориолиса, обусловленная горизонтальной составляющей (см. рисунок) этой скорости 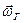 , не приводит к систематическому вращению плоскости качаний маятника Фуко, а, меняя свое направление в течение одного периода качаний, вызывает лишь малые колебания плоскости качаний маятника относительно её среднего положения. Т.о., уравнение движения маятника Фуко в системе отсчета, связанной с Землей может быть записано в виде:
, не приводит к систематическому вращению плоскости качаний маятника Фуко, а, меняя свое направление в течение одного периода качаний, вызывает лишь малые колебания плоскости качаний маятника относительно её среднего положения. Т.о., уравнение движения маятника Фуко в системе отсчета, связанной с Землей может быть записано в виде:
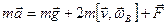 , (3.13а) где
, (3.13а) где 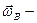 вертикальная составляющая угловой скорости собственного вращения Земли, зависящая от географической широты
вертикальная составляющая угловой скорости собственного вращения Земли, зависящая от географической широты  места, т.е.
места, т.е.
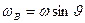 , (3.14)
, (3.14)
 угловая скорость вращения Земли (угловая частота).
угловая скорость вращения Земли (угловая частота).
Реальные опыты Фуко впервые продемонстрировал в 1850 г. в Парижской обсерватории и затем в 1851 г. в Пантеоне. Маятник имел длину 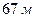 , а вес груза – металлического шара – составлял
, а вес груза – металлического шара – составлял  .
.
Находившийся в Исаакиевском соборе Ленинграда маятник Фуко, имел длину  , а его наибольшее отклонение от положения равновесия составляло
, а его наибольшее отклонение от положения равновесия составляло 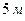 .
.
Опыты показали, что относительно Земли плоскость качаний маятника вращается вокруг вертикали рассматриваемого места в соответствии с формулой (3.14), или
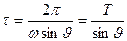 ,
,
где  время одного оборота плоскости качаний маятника, а
время одного оборота плоскости качаний маятника, а 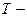 период собственного вращения Земли относительно инерциальной системы отсчета (системы Коперника).
период собственного вращения Земли относительно инерциальной системы отсчета (системы Коперника).
Если маятник отклонен в крайнее положение и отпущен безначальной скорости, то в неинерциальной системе отсчета, связанной с Землей, он будет двигаться по траектории, изображенной на рисунке слева. Сила Кориолиса все время будет изгибать траекторию маятника вправо (если смотреть в направлении движения маятника).
Несколько иная траектория получится, если маятник приведен в движения толчком из положения равновесия (правый рисунок). Траектория, по-прежнему, будет искривляться вправо, однако в крайних положениях она будет совершать плавные повороты, поскольку маятник при движении от центра приобретет под действием кориолисовой силы азимутальную скорость.
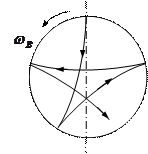 Отметим, что вследствие медленности вращения Земли наблюдатель не замечает искривления плоскости качания маятника. В обоих случаях ему кажется, что плоскость качаний вращается вокруг вертикали с угловой скоростью
Отметим, что вследствие медленности вращения Земли наблюдатель не замечает искривления плоскости качания маятника. В обоих случаях ему кажется, что плоскость качаний вращается вокруг вертикали с угловой скоростью 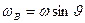 .
.
 |
В Южном полушарии вращение плоскости качаний маятника Фуко будет происходить в сторону, противоположную, наблюдаемой в Северном полушарии. На экваторе (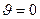 ) скорость вращения плоскости качаний маятника Фуко, как следует из (3.13а и 3.14) обращается в нуль.
) скорость вращения плоскости качаний маятника Фуко, как следует из (3.13а и 3.14) обращается в нуль.
Заметим, что результат опыта Фуко находится в согласии с предположением об инерциальности гелиоцентрической системы отсчета.
Размывы берегов рек.
 Размывы правых берегов рек в северном полушарии и левых
Размывы правых берегов рек в северном полушарии и левых
берегов рек, текущих в южном полушарии, связаны с поступательным
движением воды относительно поверхности Земли и могут быть
объяснены действием сил Кориолиса (см. рисунок).
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 5393; Нарушение авторских прав?; Мы поможем в написании вашей работы!