Инертная и гравитационная массы. Принцип эквивалентности

4.1. Инертная и гравитационная массы.

Понятие «масса» было введено в механику Ньютоном для обозначения коэффициента пропорциональности между импульсом и скоростью свободного движения тела в определении импульса

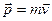, (4.1)

где 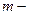постоянная для данного тела величина. Эквивалентное определение массы получается из уравнения движения классической механики – второго закона Ньютона

. (4.2)

Определенная таким образом величина является мерой инерции тела, т.к. под действием постоянной силы тело приобретает тем меньшее ускорение, чем больше его масса, и называется инерциальной или инертной массой.

Однако тела обладают не только свойствами инерции, но и способностью возбуждать в окружающем пространстве гравитационные поля (по аналогии с электрическими полями и создающими их электрическими зарядами в теории гравитации Ньютона масса выступает как источник тяготения).

Каждое тело создает поле тяготения, пропорциональное его гравитационной массе, и, в то же время, испытывает на себе воздействие поля тяготения, создаваемого другими телами, сила которого также пропорциональна его массе. Если обозначить гравитационные массы взаимодействующих тел (точечных) посредством 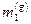и 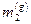, то сила гравитационного взаимодействия определяется законом Ньютона:

. (4.3)

Здесь численный коэффициент для согласования системы единиц.

Важно подчеркнуть, что инерция тел и их способность возбуждать гравитационные поля не должны рассматриваться как взаимосвязанные или, тем более, тождественные свойства. В принципе, задавая расстояние 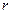и силу 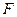в известных единицах, можно коэффициенту приписать произвольные значения и размерность, соответственно устанавливая единицы измерения гравитационной массы .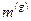

Рассматривая движение тела в поле силы тяжести Земли, можем записать

, (4.4)

где 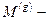масса Земли и 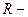ее радиус.

Физический закон, установленный Ньютоном гласит: сила гравитационного взаимодействия тел пропорциональна их инертным массам. Отсюда следует, что инертная масса тела пропорциональна его гравитационной массе.

Действительно, если тело имеет инертную массу , то под действием этой силы тяжести тело, согласно 2-му закону Ньютона, приобретает ускорение:

(4.5)

Если единицы измерения гравитационной массы выбрать такими же, как и для инертной массы, то можно положить для любого тела

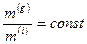
Это фундаментальный физический закон - закон эквивалентности инертной и гравитационной масс.

Галилей экспериментально установил, что все тела у поверхности Земли имеют одинаковое ускорение.

Если положить

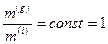
Тогда

.

Таким образом, обобщенный закон Галилея: все тела при свободном падении в одном и том же гравитационном поле приобретают одинаковое ускорение (мы уже им пользовались в предыдущем параграфе), по своему содержанию полностью соответствует принципу эквивалентности инертной и гравитационноймасс.

4.2. Опыт Этвеша.

Опыты Галилея, указывающие на эквивалентность инертной и гравитационноймасс, имели весьма малую точность. Значительно большей точности достигли Ньютон, а затем Бессель, изучая колебания маятника.

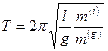
Они установили, что период малых колебаний математического маятника не зависит от материала, из которого он изготовлен. Относительная точность, с которой было установлено равенства инертной и гравитационноймасс, в опытах Бесселя составляла .

Долгое время рекордно точными были исследования венгерского физика Этвеша (1848-1919). Начиная с 1887 г. и до конца жизни он проводил опыты, в которых произвел сравнение восьми разных материалов с платиной, принятой за эталон, и установил равенство инертной и гравитационной масс с относительной точностью 5×10^-9.

m^gg

На длинной тонкой нити подвешивался стержень с прикрепленными к его концам грузами, например, из платины и меди. Стержень устанавливался перпендикулярно меридиану в месте проведения опыта (Будапешт, северной широты и восточной долготы), чтобы обеспечить одинаковые значения ускорений центробежной силы инерции (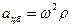) для обоих грузов, и уравновешивался в исходном положении.

Идея эксперимента: если стержень равноплечный, то он будет оставаться в равновесии в исходном положении (ось маятника перпендикулярна меридиану), если одновременно будут равны вертикальные и горизонтальные составляющие всех действующих на него сил, т.е.

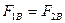(4.6а)

и

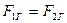. (4.6б)

В системе отсчета, связанной с Землей, на каждый груз действуют две силы:

гравитационная сила притяжения 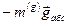, пропорциональная гравитационной массе,

и центробежная сила инерции 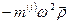, пропорциональная инертной массе.

Поэтому условие (4.6а) можно записать следующим образом

,

или

. (4.7)

Если инертная и гравитационная 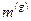массы не строго пропорциональны друг другу, т.е. , то уравнение (4.7) удовлетворяется только при .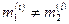

В этом случае для грузов, находящихся на стержне, ориентированном перпендикулярно меридиану, условие (4.6б) не выполняется, т.е.

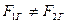
и, следовательно, должен появиться вращающий момент

(4.8)

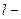(длина стержня), стремящийся закрутить нить.

В установившемся положении угол скручивания составит 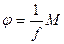, где 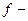модуль кручения нити. Если затем развернуть прибор на 180⁰, то момент сил и угол поворота изменят свои знаки на противоположные. Т.о., угол между двумя устойчивыми положениями стержня на скрученной нити должен составить

,

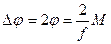что и измерялось в эксперименте.

Однако опыты Этвеша показали, что , т.е. было получено, что 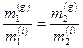, что и доказывает равенство гравитационных и инертных масс (с точностью до ).

Результаты, полученные в 1961-64 гг. американским физиком Р. Дикке с сотрудниками, а затем в 1971 г.

В. Б. Брагинским и В.И. Пановым, последовательно усовершенствовавшими опыт Этвеша, что позволило в итоге повысить точность эксперимента почти на три порядка, дают основания утверждать, что инертная и гравитационная массы равны с относительной точностью до , т.е.

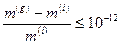. (4.9)

(Чтобы дать представление о фантастической точности проведенного эксперимента, заметим, что она соответствует процедуре взвешивания заполненного грузом корабля водоизмещением 10000 тонн с точностью до 0.01 грамма).

Ранее нами уже было отмечено, что из уравнения , где , следует вывод о том, что всякая энергия обладает инертной массой. Закон эквивалентности масс позволяет распространить это утверждение и на гравитационную массу. Всякая энергия должна обладать также и гравитационной массой. С целью проверки этого утверждения Саузернс повторил опыт Этвеша с радиоактивными веществами. В пределах точности эксперимента не было обнаружено различия между инертной и гравитационной массами. Поскольку при радиоактивных превращениях уменьшаются энергия и инертная масса источника, то результаты опыта позволяют утверждать, что пропорционально уменьшается и гравитационная масса. Т.о., равенство инертной и гравитационной масс все время соблюдается.

Если дорелятивистская физика не придавала существенного значения равенству инертной и гравитационной масс, то совсем иначе обстоит дело в теории, которая была создана и развита Эйнштейном. Принцип эквивалентности масс явился главным опытным фактом и послужил отправным пунктом при построении общей теории относительности, называемой также релятивистской теорией гравитации.

4.3. Принцип эквивалентности сил инерции и сил гравитации.

Побудительной причиной к созданию общей теории относительности (ОТО) послужили размышления о природе и возможности реализации инерциальных систем отсчета. Эйнштейн обратил внимание на следующее: невозможно понять, почему законы природы записываются в одинаковой форме только в специальных системах отсчета, которые движутся равномерно и прямолинейно относительно друг друга - ИСО. Почему вообще «вдруг» выделились инерциальные системы отсчета? Вероятно потому, что Земля – почти инерциальная система отсчета (исключая крайне слабые эффекты, обусловленные её вращением). Но как это может быть в условиях вездесущего тяготения, когда на каждое материальное тело и, в том числе на Землю, казалось бы, должны действовать внешние силы со стороны Солнца и других небесных тел? Размышления на эту тему привели Эйнштейна к гениальному выводу – инерциальность системы отсчета, связанной с Землей, объясняется свободным падением Земли в поле силы тяжести Солнца.

Гравитационные поля (поля тяготения) обладают тем свойством, что при заданных начальных условиях все тела, независимо от массы, движутся в них одинаковым образом. В частности, в поле тяготения Земли все тела приобретают одинаковое ускорение относительно любой инерциальной системы отсчета. Эйнштейн понял, что инерциальная система отсчета может быть осуществлена её свободным падением в поле силы тяжести. Такая система отсчета будет «локальной» (Земля, космический корабль и т.д.) в отличие от «глобальной» ньютоновской системы отсчета, покрывающей все пространство.

Тем же свойством, что и в поле тяготения, обладают свободно движущиеся тела, если рассматривать их движение относительно какой-либо неинерциальной системы отсчета. Тела любой массы будут обладать в этой системе отсчета одинаковым постоянным ускорением, равным и противоположным ускорению самой системы отсчета.

Т.о., равномерно ускоренная система отсчета эквивалентна в этом смысле постоянному однородному внешнему полю.

Теперь можно ответить на «простой» вопрос: почему падающая в поле земного тяготения система инерциальна? Очевидно, потому, что сила тяжести в ней компенсируется силой инерции.

Конечно, поля, которым эквивалентны неинерциальные системы отсчета, не вполне тождественны «истинным» гравитационным полям, существующим и в инерциальных системах отсчета. На бесконечном расстоянии от создающих поле тел «истинное» гравитационное поле всегда стремится к нулю. В то же время поля, эквивалентные неинерциальным системам отсчета, либо неограниченно возрастают (центробежные силы во вращающейся системе отсчета), либо остаются конечными по величине (поле, которому эквивалентна прямолинейно ускоренно движущаяся система отсчета). Кроме того, поля, которым эквивалентны неинерциальные системы отсчета, исчезают при переходе к инерциальной системе. В противоположность этому, «истинные» гравитационные поля невозможно исключить никаким выбором системы отсчета (пример – поле на бесконечности).

Однако, если рассмотреть заданный участок пространства, достаточно малый, чтобы поле в нем можно было считать однородным, то соответствующим выбором ускоренно движущейся системы отсчета можно исключить гравитационное поле на этом участке, если ускорение этой системы отсчета равно ускорению, которое приобретает частица в локальном гравитационном поле.

В этом случае силы инерции аналогичны по своему действию на тела любой массы силам тяготения.

Именно эта аналогия между силами тяготения и силами инерции явилась отправной точкой при построении общей теории относительности, созданной и окончательно сформулированной в 1916 г. Эйнштейном. Эта теория была построена чисто дедуктивным путем и лишь в дальнейшем подтверждена астрономическими наблюдениями.

Рассмотрим, как это делал Эйнштейн, пример с движущимся лифтом.

Пусть сначала лифт неподвижно висит на тросе или равномерно движется относительно Земли. Все тела в лифте находятся в поле земного тяготения. Пассажир в лифте ощущает вес собственного тела, оказывает давление на пол лифта, испытывает равную по величине и противоположно направленную реакцию со стороны пола. Подвешенный на пружине груз растягивает её своим весом. Все тела, лишенные опоры или подвеса, свободно падают относительно лифта с одним и тем же ускорением и т.д.

Вообразим теперь лифт, бесконечно удаленный от Земли и всех других небесных тел, т.е. находящийся вне каких-либо полей тяготения. Будем тянуть лифт за трос, сообщая ему постоянное ускорение . Теперь в лифте появляется единственная сила – сила инерции:

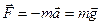. (4.10)

Под действием этой силы все тела в лифте приобретут ускорение . Груз, подвешенный на пружине, растянет её с силой 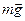, пассажир лифта будет действовать на пол с той же силой, как и в поле силы тяжести, и испытывать противодействие со стороны пола. Предоставленные самим себе тела станут «падать» с тем же ускорением .

Вывод: все механические явления и движение тел в ускоренно движущемся лифте () будут в точности такими же, как в неподвижно висящем в поле земной тяжести лифте.

Так же, как и в случае с принципом относительности Галилея, Эйнштейн распространил это утверждение не только на механические, но и на любые физические явления. Для выдвижения такой гипотезы он имел веские основания: в природе нет чисто механических явлений. Выделение «чисто механических свойств» тех или иных явлений прежде всего связано с удобством их описания. В действительности в основе каждого «механического» явления лежит громадное множество «других» явлений, которые для удобства описания мы относим к иным разделам физики.

Итак, все физические явления в равномерно ускоренном лифте будут происходить в точности так же, как в неподвижном лифте, висящем в однородном поле тяжести.

Допустим, что пассажир в лифте имеет возможность производить опыты только над телами внутри лифта и лишен возможности наблюдать «внешний мир». Замечая, что все тела в лифте падают с одним и тем же ускорением, он не может на основании только этого наблюдения решить, определить, чем вызвано это ускорение – однородным гравитационным полем, ускоренным поступательным движением лифта, или, наконец, обеими этими причинами. Т.о., никакие опыты по свободному падению тел в такой лаборатории не могут отличить однородное поле тяготения от однородного поля сил инерции.

Эйнштейн высказал предположение, что вообще никакими физическими опытами невозможно отличить однородное поле сил тяготения от однородного поля сил инерции. Это предположение, возведенное в постулат, составляет содержание принципа эквивалентности гравитационных сил и сил инерции:

Все физические явления в гравитационном поле происходят совершенно так же, как в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а начальные условия одинаковы для всех тел замкнутой системы.

В силу отмеченных в начале параграфа свойств «истинного» поля тяготения, лишь в ограниченных объемах пространства, где гравитационное поле может считаться практически однородным, оно может быть приближенно имитировано ускоренным движением системы отсчета. Поэтому принцип эквивалентности носит локальный характер.

В заключение параграфа заметим следующее.

По своим физическим действиям переносные силы инерции (поступательные и центробежные) совершенно эквивалентны ньютоновским гравитационным силам – те и другие не зависят от скоростей тел, на которые они действуют. Совершенно иначе ведут себя силы Кориолиса – они возникают только при движении тела и пропорциональны его скорости. Тем не менее, эквивалентность инертной и гравитационной масс делает целесообразным объединение гравитационного поля и поля всех сил инерции в единое поле, что и происходит в общей теории относительности. Поле, являющееся результатом такого объединения сохраняет название гравитационного поля, а сила инерции становится частным случаем сил этого поля. Уравнения гравитационного поля в общей теории относительности называются уравнениями Эйнштейна. Закон всемирного тяготения Ньютона содержится в уравнениях Эйнштейна и носит приближенный характер уже потому, что в его основе лежит предположение о мгновенном распространении взаимодействий.

Физические законы в НИСО в присутствии сил инерции записываются также как в ИСО в присутствии поля тяготения – это фундаментальный принцип эквивалентности, сформулированный в виде общего принципа относительности.

Основная идея ОТО.

Можно сказать, что основное содержание ОТО содержится в ответе на вопрос – как гравитационное поле воздействует на свойства пространства и времени. Чтобы разобраться с этим вопросом, воспользуемся принципом эквивалентности.

Поведение часов и масштабов в присутствии полей тяготения.

Рассмотрим течение времени и поведение масштабов длин с точки зрения наблюдателей, связанных с инерциальной и неинерциальной системами отсчета.

Пример Эйнштейна.

Пусть диск радиусом 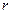вращается с постоянной угловой скоростью вокруг оси симметрии, перпендикулярной его плоскости.

Установим одинаковым образом проградуированные часы

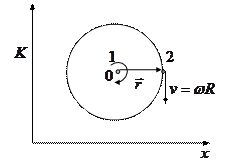в центре, по радиусу и на краю диска.

Центр диска покоится в некоторой инерциальной системе

отсчета. С точки зрения наблюдателя, находящегося в ИСО,

ход часов будет замедляться по мере их удаления от центра

диска.

, , .

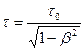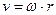Для наблюдателя из НИСО ход часов также будет

замедляться по мере их приближения к краю, но он

объяснит это действием центробежной силы инерции

, (4.11)

или, с точки зрения общей теории относительности, наличием гравитационного поля напряженностью 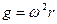, возрастающего от центра к краю диска.

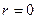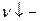Итак, в этом гравитационном поле часы в центре диска (, слабое поле) показывают такое же время, как и любые другие часы, помещенные вдоль оси (ИСО), и максимально замедляют свой ход на краю диска (, сильное поле). Можно сказать, что часы идут быстрее или медленнее в зависимости от величины гравитационного поля, в которое они помещены (период растет; частота падает).

Посмотрим теперь, как ведут себя масштабы. Если мы остановим диск, то, с точки зрения обоих наблюдателей, отношение длины окружности диска к его диаметру :

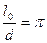. (4.12)

Пусть диск вращается с угловой скоростью 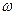, т.е. теперь линейный элемент окружности диска в окрестности точки 2 движется относительно наблюдателя из ИСО, находящегося в точке 1, со скоростью 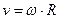. Если 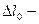линейный элемент окружности покоящегося (невращающегося) в 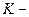системе диска, то

. (4.13)

В то же самое время расстояние между точками 1 и 2, равное , не претерпевает изменения в силу того, что «поперечные» (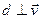) размеры тел в соответствии с постулатами СТО сохраняются.

Тогда, для вращающегося диска, с точки зрения наблюдателя из ИСО, находящегося в точке 1, выполняется равенство

, (4.14)

откуда неизбежно следует

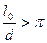. (4.15)

Для наблюдателя из НИСО, вращающего вместе с диском, этот эффект связан с наличием возрастающего от центра к краю гравитационного (в расширенном толковании) поля, которое, действуя на пространство, «деформирует» последнее с точки зрения евклидовой геометрии.

Рассмотрим ещё один пример.

Пусть в некоторый момент времени часы начинают движение относительно инерциальной 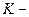системы отсчета и движутся с постоянным ускорением . Если часы идут одинаково с любыми часами во всякой мгновенно сопутствующей инерциальной системе отсчета, то промежуток времени, определенный по неподвижным ) и движущимся () часам, связан формулой

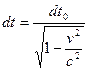. (4.16)

Единственной видимой причиной замедления времени является движение часов.

Если расстояние, пройденное часами, то их скорость в 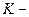системе

. (4.17)

Тогда

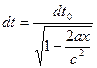. (4.18)

Теперь обратимся к неинерциальной системе отсчета, движущейся вместе с часами . В этой системе отсчета часы неподвижны, но есть силы инерции, которые в соответствии с принципом относительности неотличимы от сил гравитации.

Положим применительно к земному тяготению и введем в рассмотрение гравитационный потенциал

, (4.19)

тогда, взяв модуль ускорения, можем переписать (4.18) в виде

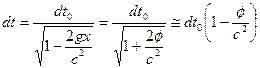. (4.20)

Отсюда получаем

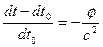, (4.21)

здесь и 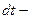промежутки времени, измеренные по часам, расположенным в точках с нулевым гравитационным потенциалом и с гравитационным потенциалом , соответственно.

Для двух точек гравитационного поля с различным потенциалом:

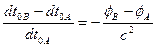, (4.22)

Т.о., часы в гравитационном поле идут тем медленнее, тем выше гравитационный потенциал точки, в которой они находятся. Например, на поверхности Земли ; на Солнце - .

В 1976 г. группа ученых Мэрилендского университета провела измерения на борту самолета, летавшего в течение 14 часов на высоте 10 км, в котором находились сверхточные цезиевые часы. Эталонные часы оставались на поверхности Земли. Рассчитанные поправки составили: кинематическая - 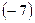нс; гравитационная - 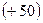нс. Теоретические предсказания оправдались с возможной погрешностью (!).

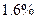Именно сходство движения тел в НИСО с учетом сил инерции и в ИСО при наличии гравитации привело Эйнштейна к выводу, что пространство и время, находящиеся под воздействием гравитационного поля, образуют единое искривленное 4^х-мерное пространство-время, для описания которого нужна особая (неевклидова) геометрия.

Гравитация и геометрия.

В отсутствии тяготения в пространстве-времени СТО движение тела по инерции изображается прямой линией, или, на математическом языке, экстремальной (геодезической) линией.

Согласно эйнштейновской теории тяготения в поле тяготения тела также движутся по геодезическим линиям в пространстве-времени, которое искривлено, т.е. геодезические линии – не прямые, и геометрия такого пространства-времени – уже неевклидова. В заданном поле тяготения все тела, независимо от их массы и состава, при одинаковых начальных условиях будут двигаться по одним и тем же геодезическим линиям, т.е. совершенно одинаково. Наблюдатель воспримет это движение как движение по искривленным траекториям в трехмерном пространстве-времени с переменной скоростью.

Кривизна пространства-времени создается источниками гравитационного поля. При этом тяготение, т.е. искривление пространства-времени, определяется не только массой вещества, слагающего тело, но и всеми видами энергии, присутствующими в системе. Эта идея явилась обобщением на случай теории тяготения сформулированного в СТО принципа эквивалентности массы и энергии , т.е. тяготение зависит не только от распределения масс в пространстве, но и от их движения, от давления и натяжений в телах, от электромагнитного и всех других физических полей.

Проще всего представить неевклидову геометрию в двумерном случае.

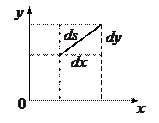Соответствующие координаты были изобретены великим немецким математиком Гауссом с целью измерить площади земельных участков, расположенных на неровной местности.

Если в плоской евклидовой геометрии длина отрезка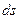

в прямоугольных координатах 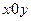определяется из уравнения

,

а в косоугольных координатах

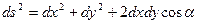
и в обоих случаях суммы углов треугольников всегда равны

,

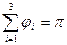то в гауссовых координатах, когда в общем случае поверхность неплоская,

длина отрезка 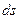записывается как

,

где коэффициенты 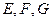зависят от координат точки на поверхности

и сумма углов треугольника

.

Отрезок 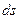на гауссовой поверхности – геодезическая линия (его длина – кратчайшее расстояние между двумя точками на гауссовой поверхности).

В общем случае (для поверхности любой кривизны) можно записать

. (4.23)

Если коэффициенты зависят от координат, то никаким образом нельзя выразить длину отрезка 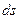, заданную в криволинейных координатах, в «плоских» евклидовых координатах. Набор коэффициентов может характеризовать геометрические свойства пространства.

Ученик Гаусса Риман показал, что та же картина имеет место и в трехмерном, и в четырехмерном пространствах. Только вместо относительно простых функций необходимо использовать гораздо более сложные.

Т.о., в искривленном неевклидовом пространстве тела перемещаются по геодезическим (экстремальным) линиям, которые представляют собой 4^х-мерное обобщение «прямых» псевдоевклидовой геометрии пространства Минковского. Именно по таким геодезическим линиям вместо свободного движения происходит свободное падение тел – камня на Земле, планеты вокруг Солнца.

Т.о., специальная теория относительности является теорией физических процессов в плоском пространстве-времени (пространстве-времени Минковского). В общей теории относительности пространство-время не плоское, а искривленное. В таком пространстве-времени (в не малых, т.е. конечных областях) нельзя ввести декартовы координаты, поэтому становится неизбежным использование криволинейных координат. Тогда в конечных областях искривленного пространства-времени квадрат четырехмерного «расстояния» (интервала) записывается в криволинейных координатах общей квадратичной формой:

, (4.24)

где 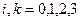; 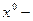временная координата; произвольные пространственные координаты; по дважды встречающимся индексам, как и ранее, производится суммирование.

С физической точки зрения переход к произвольным координатам означает и переход от ИСО к системе отсчета, вообще говоря, движущейся с ускорением (в общем случае разным в разных точках), деформирующейся и вращающейся с использованием в этой системе отсчета недекартовых координат и произвольно идущих часов.

Зная 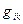как функции четырех координат, можно определить все геометрические свойства пространства-времени. Говорят, что величины 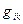определяют метрику пространства-времени, а совокупность всех 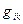называют метрическим тензором. С помощью 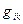вычисляют темп течения времени в разных точках системы отсчета и расстояния между точками в трехмерном пространстве. Формула для вычисления бесконечно малого интервала времени по часам, покоящимся в системе отсчета, имеет вид:

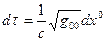. (4.25)

Это соотношение определяет промежутки собственного времени для данной точки пространства по изменению координаты .

При наличии поля тяготения величина 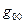разная в различных точках, следовательно, темп течения времени зависит от гравитационного поля. Оказывается, что чем сильнее поле, тем медленнее течет время по сравнению с течением времени для наблюдателя, находящегося вне поля.

Математическим аппаратом ОТО является тензорное исчисление. Законы природы записываются в произвольных криволинейных координатах (т.е. в произвольных системах отсчета) в виде, формально пригодном в любой четырехмерной системе отсчета (как говорят, в ковариантном виде).

Основная задача теории тяготения – определение гравитационного поля, что соответствует в ОТО нахождению геометрии пространства-времени. Эта последняя задача сводится к нахождению метрического тензора .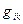

В ОТО Эйнштейн установил связь между распределением и движением материи, с одной стороны, и пространственно-временной метрикой 4^х-мерного пространства-времени с другой. Уравнения тяготения Эйнштейна, связывающие величины 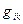с величинами, характеризующими материю, создающую поле, имеют вид:

. (4.26)

называется скалярной кривизной пространства; величины определяются из уравнений

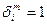, где символ Кронекера: при ; при .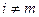

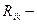так называемый тензор Риччи, выражающийся через 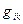, его первые и вторые производные по координатам.

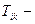тензор энергии-импульса материи, компоненты которого выражаются через плотность, потоки импульса и другие величины, характеризующие материю и её движение (под физической материей подразумевается обычное вещество и физические поля).

Отметим, что в отличие от уравнений Ньютона, уравнения (4.26) ОТО нелинейны и не удовлетворяют принципу суперпозиции.

Решение уравнений Эйнштейна приводит к совместному определению движения материи, создающей поле, и к вычислению самого поля. Существенно, что уравнения поля тяготения содержат в себе и уравнения движения масс в поле тяготения. С физической точки зрения это соответствует тому, что в ОТО материя создает искривление пространства-времени, которое влияет на движение материи, создающей искривление.

Если же искривление пространства мало, то появляется возможность использовать для описания движения тела евклидово пространство с учетом гравитационного поля, задаваемого законом всемирного тяготения Ньютона. Уравнения Эйнштейна (4.26) приближенно переходят в уравнения теории Ньютона (4.27) и (4.29).

1. У равнение Пуассона

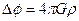. (4.27)

Функция задает распределение плотности вещества в пространстве; как и всюду, гравитационная постоянная; оператор Лапласа.

Уравнение (4.27) служит для нахождения гравитационного потенциала , градиент которого определяет напряженность потенциального гравитационного поля

. (4.28)

2. Уравнение движения тела в поле тяготения (II закон Ньютона)

, (4.29)

причем выполняется принцип эквивалентности масс: .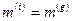

Экспериментальная проверка общей теории относительности.

К моменту создания окончательной формулировки ОТО (1915 г.) сам Эйнштейн указал три знаменитых «критических» эффекта, которые могут служить для проверки теории: гравитационное смещение спектральных линий («Если гравитационного смещения спектральных линий не существует, то ОТО несостоятельна» - Эйнштейн, 1920 г.), отклонение световых лучей в поле Солнца и смещение перигелия Меркурия. Хотя основополагающим экспериментом, конечно же, является опытная проверка принципа эквивалентности масс.

Если ОТО верна, то должно существовать гравитационное смещение спектральных линий. Т.е., если источник и приемник расположены в точках с разным гравитационным потенциалом, то должно выполняться соотношение

.

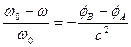Такой сдвиг впервые наблюдал Адамс в 1924 г., исследуя спектры спутника Сириуса - белого карлика Сириус-В. Для света, приходящего от Солнца к Земле (против гравитационного поля, более сильного около Солнца) наблюдается гравитационный сдвиг частоты , что блестяще подтверждает теорию.

Теория предсказывает искривление луча света при прохождении вблизи массивных тел. Причем этот результат следует и из ньютоновской теории тяготения и из общей теории относительности. Различие состоит в том, что с точки зрения ОТО этот эффект должен быть вдвое большим. Многочисленные наблюдения прохождения света от звезд, проводившиеся во время полных солнечных затмений, подтвердили предсказания ОТО (отклонение луча на 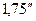у края солнечного диска) с точностью 20%. Гораздо большая точность (не хуже 6%) была достигнута с помощью современной техники наблюдения внеземных точечных источников, излучающих в радиодиапазоне.

Тесно связан с только что рассмотренным и другой эффект – бо^/льшая длительность распространения света в поле тяготения, чем это дают формулы без учета эффектов общей теории относительности. ОТО предсказывает дополнительную задержку луча, проходящего вблизи Солнца около 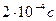. Эксперименты проводились методом радиолокации Меркурия и Венеры во время их прохождения за диском Солнца, с также с помощью ретрансляции радиосигналов космическими кораблями. Предсказания теории были подтверждены с точностью не хуже, чем 2%.

Ещё одним эффектом, предсказываемым ОТО, является медленный дополнительный, (т.е. который не может быть объяснен гравитационными возмущениями со стороны других планет Солнечной системы) поворот в эллиптических орбитах планет, движущихся вокруг Солнца. Наибольшую величину этот эффект имеет для орбиты Меркурия и составляет 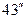в столетие. Это предсказание подтверждено экспериментально с точностью до 1%.

Ограничения применимости теории тяготения Эйнштейна.

ОТО – неквантовая теория. Она подобна в этом отношении классической электродинамике Максвелла. Однако из общих рассуждений следует, что, так же как и электромагнитное поле, гравитационное поле должно подчиняться квантовым законам. В противном случае возникли бы противоречия с принципом неопределенности для электронов, фотонов и т.д.

Применение квантовой теории к гравитации показывает, что гравитационные волны можно рассматривать как поток квантов – гравитонов, представляющих собой электрически нейтральные частицы с нулевой массой покоя и спином, равным (в единицах ).

В подавляющем большинстве процессов, мыслимых во Вселенной и наблюдаемых в лабораторных условиях, квантовые эффекты гравитации чрезвычайно слабы, что позволяет обоснованно пользоваться общей теорией относительности. Однако там, где искривления пространства-времени очень велики, т.е. вблизи сингулярностей поля тяготения, квантовые эффекты должны стать существенными, и ОТО неприменима.

Сингулярные состояния возникают в ходе гравитационного коллапса, сингулярность в прошлом была в расширяющейся Вселенной. Последовательной квантовой теории, описывающей такие явления, пока не существует. В то же время можно предположить, что при энергиях частиц, соответствующих столь экстремальным состояниям (), все виды физических взаимодействий будут проявляться как единое взаимодействие.

Дата добавления: 2014-01-05