По­ня­тие о ста­ти­сти­че­ской и кор­ре­ля­ци­он­ной свя­зи

Раз­ли­ча­ют два ти­па свя­зей ме­ж­ду раз­лич­ны­ми яв­ле­ния­ми и их при­зна­ка­ми: функ­цио­наль­ную или же­ст­ко де­тер­ми­ни­ро­ван­ную, с од­ной сто­ро­ны, и ста­ти­сти­че­скую или сто­хас­ти­че­ски де­тер­ми­ни­ро­ван­ную - с дру­гой. Строго оп­ре­де­лить раз­ли­чие этих двух ти­пов свя­зи мож­но то­гда, ко­гда они по­лу­ча­ют ма­те­ма­ти­че­скую фор­му­ли­ров­ку. Для про­сто­ты бу­дем го­во­рить о свя­зи двух яв­ле­ний или двух при­зна­ков, ма­те­ма­ти­че­ски ото­бра­жае­мой в фор­ме урав­не­ния свя­зи двух пе­ре­мен­ных.

Ес­ли с из­ме­не­ни­ем зна­че­ния од­ной из пе­ре­мен­ных вто­рая из­ме­ня­ет­ся строго оп­ре­де­лен­ным об­ра­зом, т.е. зна­че­нию од­ной пе­ре­мен­ной со­от­вет­ст­ву­ет од­но или не­сколь­ко точ­но за­дан­ных зна­че­ний дру­гой пе­ре­мен­ной, связь ме­ж­ду ни­ми яв­ля­ет­ся функ­цио­наль­ной.

Не­ред­ко го­во­рят о стро­гом со­от­вет­ст­вии лишь од­но­го зна­че­ния вто­рой из пе­ре­мен­ных ка­ж­до­му зна­че­нию пер­вой из них, но это не­вер­но. На­при­мер, связь ме­ж­ду x и y яв­ля­ет­ся стро­го функ­цио­наль­ной ес­ли y=(x; но зна­че­нию x=4 со­от­вет­ст­ву­ет не од­но, а два зна­че­ния; y1=2 и y2=-2. Урав­не­ния бо­лее вы­со­ких сте­пе­ней мо­гут иметь не­сколь­ко кор­ней, связь ра­зу­ме­ет­ся ос­та­ет­ся функ­цио­наль­ной.

Функ­цио­наль­ная связь двух ве­ли­чин воз­мож­на лишь при ус­ло­вии, что вто­рая из них за­ви­сит толь­ко от пер­вой и ни от че­го бо­лее. В ре­аль­ной при­ро­де та­ких свя­зей нет; они яв­ля­ют­ся лишь аб­ст­рак­ция­ми, по­лез­ны­ми и не­об­хо­ди­мы­ми при ана­ли­зе яв­ле­ний, но уп­ро­щаю­щи­ми ре­аль­ность. Функ­цио­наль­ная за­ви­си­мость дан­ной ве­ли­чи­ны y от мно­гих фак­то­ров x1, x2,... xk воз­мож­на толь­ко в том слу­чае, ес­ли ве­ли­чи­на y все­гда за­ви­сит толь­ко от пе­ре­мен­но­го на­бо­ра фак­то­ров x1, x2,... xk и ни от че­го боль­ше. Ме­ж­ду тем все яв­ле­ния и про­цес­сы ре­аль­но­го ми­ра свя­за­ны ме­ж­ду со­бой, и нет та­ко­го ко­неч­но­го чис­ла пе­ре­мен­ных k, ко­то­рые аб­со­лют­но пол­но оп­ре­де­ля­ли бы со­бой за­ви­си­мую ве­ли­чи­ну y. Сле­до­ва­тель­но, мно­же­ст­вен­ная функ­цио­наль­ная за­ви­си­мость пе­ре­мен­ных есть то­же аб­ст­рак­ция, уп­ро­щаю­щая ре­аль­ность.

Од­на­ко в нау­ке ус­пеш­но ис­поль­зу­ют пред­став­ле­ние свя­зей как функ­цио­наль­ных не толь­ко в ана­ли­ти­че­ских це­лях, но не­ред­ко и в це­лях про­гно­зи­ро­ва­ния. Это воз­мож­но по­то­му, что в не­ко­то­рых про­стых сис­те­мах ин­те­ре­сую­щая нас пе­ре­мен­ная за­ви­сит в ос­нов­ном (ска­жем на 99% или да­же на 99.99%) от не­мо­но­гих дру­гих пе­ре­мен­ных или толь­ко от од­ной пе­ре­мен­ной. То есть связь в та­кой не­слож­ной сис­те­ме яв­ля­ет­ся хо­тя и не аб­со­лют­но функ­цио­наль­ной, но прак­ти­че­ски очень близ­кой к та­ко­вой. Так, на­при­мер, дли­на го­да (пе­ри­од об­ра­ще­ния Зем­ли во­круг Солн­ца) поч­ти функ­цио­наль­но за­ви­сит толь­ко от мас­сы Солн­ца и расстояния Зем­ли от не­го. На са­мом де­ле она за­ви­сит в очень сла­бой сте­пе­ни и от масс, и расстояния дру­гих пла­нет от Зем­ли, но вно­си­мые ими (и тем бо­лее в мил­лио­ны раз бо­лее да­ле­ки­ми звез­да­ми) ис­ка­же­ния функ­цио­наль­ной свя­зи для всех прак­ти­че­ских це­лей, кро­ме кос­мо­нав­ти­ки, пре­неб­ре­жи­мо ма­лы.

Сто­хас­ти­че­ски де­тер­ми­ни­ро­ван­ная связь не име­ет ог­ра­ни­че­ний и ус­ло­вий, при­су­щих функ­цио­наль­ной свя­зи. Ес­ли с из­ме­не­ни­ем зна­че­ния од­ной пе­ре­мен­ной вто­рая мо­жет в оп­ре­де­лен­ных при­де­лах при­ни­мать лю­бые зна­че­ния с ве­ро­ят­но­стя­ми, но ее сред­нее зна­че­ние или иные ста­ти­сти­че­ские (мас­со­вые) ха­рак­те­ри­сти­ки из­ме­ня­ют­ся по оп­ре­де­лен­но­му за­ко­ну - связь яв­ля­ет­ся ста­ти­сти­че­ской. Ины­ми сло­ва­ми, при ста­ти­сти­че­ской свя­зи раз­ным зна­че­ни­ям од­ной пе­ре­мен­ной соответствуют раз­ные рас­пре­де­ле­ния зна­че­ний дру­гой пе­ре­мен­ной.

В на­стоя­щее вре­мя нау­ка не зна­ет бо­лее ши­ро­ко­го оп­ре­де­ле­ния свя­зи. Все свя­зи, ко­то­рые мо­гут быть из­ме­ре­ны и вы­ра­же­ны чис­лен­но, под­хо­дят под оп­ре­де­ле­ние “ста­ти­сти­че­ской свя­зи”, в том чис­ле и функ­цио­наль­ные. По­след­ние пред­став­ля­ют со­бой ча­ст­ный слу­чай ста­ти­сти­че­ских свя­зей, ко­гда зна­че­ни­ям од­ной пе­ре­мен­ной соответствуют “рас­пре­де­ле­ния” зна­че­ний вто­рой, со­стоя­щие из од­но­го или не­сколь­ких зна­че­ний и имею­щие ве­ро­ят­ность, рав­ную еди­ни­це.

Кор­ре­ля­ци­он­ной свя­зью на­зы­ва­ют важ­ней­ший ча­ст­ный слу­чай ста­ти­сти­че­ской свя­зи, со­стоя­щий в том, что раз­лич­ным зна­че­ни­ям од­ной пе­ре­мен­ной со­от­вет­ст­ву­ют раз­лич­ные сред­ние зна­че­ния дру­гой. С из­ме­не­ни­ем зна­че­ния x за­ко­но­мер­ным об­ра­зом из­ме­ня­ет­ся сред­нее зна­че­ние при­зна­ка y; в то вре­мя как в ка­ж­дом от­дель­ном слу­чае зна­че­ние при­зна­ка y (с раз­лич­ны­ми сте­пе­ня­ми ве­ро­ят­но­сти) мо­жет при­ни­мать мно­же­ст­во раз­лич­ных зна­че­ний.

Ес­ли же с из­ме­не­ни­ем зна­че­ния при­зна­ка x сред­нее зна­че­ние при­зна­ка y не из­ме­ня­ет­ся за­ко­но­мер­ным об­ра­зом, но за­ко­но­мер­но из­ме­ня­ет­ся дру­гая ста­ти­сти­че­ская ха­рак­те­ри­сти­ка (по­ка­за­те­ли ва­риа­ции, асимметрии, экс­цес­са и т.п.), то связь яв­ля­ет­ся не кор­ре­ля­ци­он­ной, а ста­ти­сти­че­ской.

Ста­ти­сти­че­ская связь ме­ж­ду дву­мя при­зна­ка­ми (пе­ре­мен­ны­ми ве­ли­чи­на­ми) пред­по­ла­га­ет, что ка­ж­дый из них име­ет слу­чай­ную ва­риа­цию ин­ди­ви­ду­аль­ных зна­че­ний от­но­си­тель­но сред­ней ве­ли­чи­ны. Ес­ли же та­кую ва­риа­цию име­ет лишь один из при­зна­ков, а зна­че­ния дру­го­го яв­ля­ют­ся стро­го де­тер­ми­ни­ро­ван­ны­ми, то го­во­рят лишь о рег­рес­сии, но не о ста­ти­сти­че­ской (тем бо­лее кор­ре­ля­ци­он­ной) свя­зи. На­при­мер, при ана­ли­зе ди­на­ми­че­ских ря­дов мож­но из­ме­рять рег­рес­сию уров­ней ря­да уро­жай­но­сти (имею­щих слу­чай­ную из­мен­чи­вость) на но­ме­ра лет. Но нель­зя го­во­рить о кор­ре­ля­ции ме­ж­ду ни­ми и при­ме­нять по­ка­за­те­ли кор­ре­ля­ции с со­от­вет­ст­вую­щей им ин­тер­пре­та­ци­ей.

Са­мо сло­во кор­ре­ля­ция ввел в упот­реб­ле­ние в ста­ти­сти­ку анг­лий­ский био­лог и ста­ти­стик Френ­сис Галь­тон в кон­це XIX ве­ка. То­гда оно пи­са­лось как “corelation” (соответствие), но не про­сто “связь” (relation), а “как бы связь”, т.е. связь, но не в при­выч­ной функ­цио­наль­ной фор­ме. В нау­ке во­об­ще, а имен­но в па­лео­нто­ло­гии, тер­мин “кор­ре­ля­ция” при­ме­нял еще рань­ше, в кон­це XYIIIв зна­ме­ни­тый фран­цуз­ский па­лео­нто­лог Жорж Кю­вье. Он ввел да­же “за­кон кор­ре­ля­ции” час­тей и ор­га­нов жи­вот­ных. “За­кон кор­ре­ля­ции” по­мо­га­ет вос­ста­но­вить по най­ден­ным в рас­коп­ках че­ре­пу, кос­тям и т.д. об­лик все­го жи­вот­но­го и его ме­сто в сис­те­ме: ес­ли че­реп с ро­га­ми, то это бы­ло тра­во­яд­ное жи­вот­ное, а его ко­неч­но­стя­ми бы­ли ко­пы­та; ес­ли же ла­па с ког­тя­ми - то хищ­ное жи­вот­ное без ро­гов, но с круп­ны­ми клы­ка­ми.

Кор­ре­ля­ци­он­ная связь ме­ж­ду при­зна­ка­ми мо­жет воз­ни­кать раз­лич­ны­ми пу­тя­ми. Важ­ней­ший путь - при­чин­ная за­ви­си­мость ре­зуль­та­тив­но­го при­зна­ка (его ва­риа­ции) от вариации фак­тор­но­го при­зна­ка. На­при­мер, при­знак x - балл оцен­ки пло­до­ро­дия почв, при­знак y - уро­жай­ность сель­ско­хо­зяй­ст­вен­ной куль­ту­ры. Здесь со­вер­шен­но яс­но ло­ги­че­ски, ка­кой при­знак яв­ля­ет­ся не­за­ви­си­мой пе­ре­мен­ной (фак­тор) x, ка­кой - за­ви­си­мой пе­ре­мен­ной (ре­зуль­тат) y.

Со­вер­шен­но иная ин­тер­пре­та­ция нуж­на при изу­че­нии кор­ре­ля­ци­он­ной свя­зи ме­ж­ду дву­мя след­ст­вия­ми од­ной при­чи­ны. Из­вес­тен клас­си­че­ский при­мер, при­ве­ден­ный круп­ней­шим ста­ти­сти­ком России на­ча­ла XXв А.А. Чу­про­вым: ес­ли в ка­че­ст­ве при­зна­ка x взять чис­ло по­жар­ных ко­манд в го­ро­де, а за при­знак y - сум­му убыт­ков за год в го­ро­де от по­жа­ров, то ме­ж­ду при­зна­ка­ми x и y в со­во­куп­но­сти го­ро­дов Рос­сии су­ще­ст­вен­ная пря­мая кор­ре­ля­ция; в сред­нем, чем боль­ше по­жар­ни­ков в го­ро­де, тем боль­ше и убыт­ков от по­жа­ров. Уж не за­ни­ма­лись ли под­жи­га­тель­ст­вом из бо­яз­ни по­те­рять ра­бо­ту? Но де­ло в дру­гом. Дан­ную кор­ре­ля­цию нель­зя ин­тер­пре­ти­ро­вать как связь при­чи­ны и след­ст­вия; оба при­зна­ка - след­ст­вия об­щей при­чи­ны - раз­ме­ра го­ро­да. Впол­не ло­гич­но, что в круп­ных го­ро­дах боль­ше по­жар­ных час­тей, но и боль­ше по­жа­ров, и убыт­ков от них за год, чем в мел­ких го­ро­дах.

Тре­тий путь воз­ник­но­ве­ния кор­ре­ля­ции - взаи­мо­связь при­зна­ков, ка­ж­дый из ко­то­рых и при­чи­на и след­ст­вие. Та­ко­ва, на­при­мер, кор­ре­ля­ция ме­ж­ду уров­ня­ми про­из­во­ди­тель­но­сти тру­да ра­бо­чих и уров­нем оп­ла­ты 1 ча­са тру­да (та­риф­ной сет­ки). С од­ной сто­ро­ны, уро­вень зар­пла­ты - след­ст­вие про­из­во­ди­тель­но­сти тру­да: чем она вы­ше, тем вы­ше и оп­ла­та. Но с дру­гой сто­ро­ны, ус­та­нов­лен­ные рас­цен­ки иг­ра­ют сти­му­ли­рую­щую роль: при пра­виль­ной сис­те­ме оп­ла­ты они вы­сту­па­ют в ка­че­ст­ве фак­то­ра, от ко­то­ро­го за­ви­сит про­из­во­ди­тель­ность тру­да. В та­кой сис­те­ме при­зна­ков до­пус­ти­мы обе по­ста­нов­ки за­да­чи; ка­ж­дый при­знак мо­жет вы­сту­пать и в ро­ли не­за­ви­си­мой пе­ре­мен­ной x, и в ка­че­ст­ве за­ви­си­мой пе­ре­мен­ной y.

Ус­ло­вия при­ме­не­ния и ог­ра­ни­че­ния кор­ре­ля­ци­он­но-рег­рес­си­он­но­го ме­то­да.

По­сколь­ку кор­ре­ля­ци­он­ная связь яв­ля­ет­ся ста­ти­сти­че­ской, пер­вым ус­ло­ви­ем воз­мож­но­сти ее изу­че­ния яв­ля­ет­ся об­щее ус­ло­вие вся­ко­го ста­ти­сти­че­ской ис­сле­до­ва­ния: на­ли­чие дан­ных по дос­та­точ­но боль­шой со­во­куп­но­сти яв­ле­ний. По от­дель­ным яв­ле­ни­ям мож­но по­лу­чить со­вер­шен­но не­пра­виль­ное пред­став­ле­ние о свя­зи при­зна­ков, ибо в ка­ж­дом от­дель­ном яв­ле­нии зна­че­ния при­зна­ков кро­ме за­ко­но­мер­ной со­став­ляю­щей име­ют слу­чай­ное от­кло­не­ние (ва­риа­цию). На­при­мер, срав­ни­вая зна­ния био­ло­гии сту­ден­та-хи­ми­ка и сту­ден­та-био­ло­га мож­но об­на­ру­жить, что зна­ния пер­во­го об­шир­нее. Но ес­ли срав­ни­вать всех сту­ден­тов фа­куль­те­тов, то ока­жет­ся, что зна­ния сту­ден­тов-био­ло­гов все-та­ки не­множ­ко боль­ше.

Ка­кое имен­но чис­ло на­блю­де­ний дос­та­точ­но для ана­ли­за кор­ре­ля­ци­он­ной и во­об­ще ста­ти­сти­че­ской свя­зи, за­ви­сит от це­ли ана­ли­за, тре­буе­мой точ­но­сти и на­деж­но­сти па­ра­мет­ров свя­зи, от чис­ла фак­то­ров с ко­то­ры­ми кор­ре­ля­ция изу­ча­ет­ся. Обыч­но счи­та­ют, что чис­ло на­блю­де­ний долж­но быть не ме­нее чем в 5-6 раз, а луч­ше не ме­нее чем в 10 раз боль­ше чис­ла фак­то­ров. Еще луч­ше ес­ли чис­ло на­блю­де­ний в не­сколь­ко де­сят­ков или в сот­ни раз боль­ше чис­ла фак­то­ров, то­гда за­кон боль­ших чи­сел, дей­ст­вуя в пол­ную си­лу, обес­пе­чи­ва­ет эф­фек­тив­ное взаи­мо­по­га­ше­ние слу­чай­ных от­кло­не­ний от за­ко­но­мер­но­го ха­рак­те­ра свя­зи при­зна­ков.

Вто­рым ус­ло­ви­ем за­ко­но­мер­но­го про­яв­ле­ния кор­ре­ля­ци­он­ной свя­зи слу­жит ус­ло­вие, обес­пе­чи­ваю­щее на­деж­ное вы­ра­же­ние за­ко­но­мер­но­сти в сред­ней ве­ли­чи­не. Кро­ме уже ука­зан­но­го боль­шо­го чис­ла еди­ниц со­во­куп­но­сти для это­го не­об­хо­ди­ма дос­та­точ­но ка­че­ст­вен­ная од­но­род­ность со­во­куп­но­сти. На­ру­ше­ние это­го ус­ло­вия мо­жет из­вра­тить па­ра­мет­ры кор­ре­ля­ции. На­при­мер, наблюдается прямая зависимость между численностью животных и площадью на которой она подсчитывалась. Однако, есть колониальные животные и есть одиночные и, если исследовать зависимость между общим числом животных всех видов и площадью, то получится совершенно другая зависимость.

Ино­гда как ус­ло­вие кор­ре­ля­ци­он­но­го ана­ли­за вы­дви­га­ют не­об­хо­ди­мость под­чи­не­ния рас­пре­де­ле­ния со­во­куп­но­сти по ре­зуль­та­тив­но­му и фак­тор­ным при­зна­кам нор­маль­но­му за­ко­ну рас­пре­де­ле­ния ве­ро­ят­но­стей. Это ус­ло­вие свя­за­но с при­ме­не­ни­ем ме­то­да наи­мень­ших квад­ра­тов при рас­че­те па­ра­мет­ров кор­ре­ля­ции: толь­ко при нор­маль­ном рас­пре­де­ле­нии ме­тод наи­мень­ших квад­ра­тов да­ет оцен­ку па­ра­мет­ров, от­ве­чаю­щую прин­ци­пам мак­си­маль­но­го прав­до­по­до­бия. На прак­ти­ке эта пред­по­сыл­ка ча­ще все­го вы­пол­ня­ет­ся при­бли­жен­но, но и то­гда ме­тод наи­мень­ших квад­ра­тов да­ет не­пло­хие ре­зуль­та­ты.

Од­на­ко при зна­чи­тель­ном от­кло­не­нии рас­пре­де­ле­ний при­зна­ков от нор­маль­но­го за­ко­на нель­зя оце­ни­вать на­деж­ность вы­бо­роч­но­го ко­эф­фи­ци­ен­та кор­ре­ля­ции, ис­поль­зуя па­ра­мет­ры нор­маль­но­го рас­пре­де­ле­ния ве­ро­ят­но­сти или рас­пре­де­ле­ния Стью­ден­та.

Еще од­ним спор­ным во­про­сом яв­ля­ет­ся до­пус­ти­мость при­ме­не­ния кор­ре­ля­ци­он­но­го ана­ли­за к функ­цио­наль­но свя­зан­ным при­зна­кам. Без­ус­лов­но нель­зя про­во­дить кор­ре­ля­ци­он­ный ана­лиз в тех слу­ча­ях ко­гда за­ве­до­мо из­вест­но, что ме­ж­ду па­ра­мет­ра­ми су­ще­ст­ву­ет же­ст­ко де­тер­ми­ни­ро­ван­ная связь. На­при­мер, чис­ло ба­бо­чек и чис­ло крыль­ев у них. Од­на­ко, по­лез­но про­во­дить кор­ре­ля­ци­он­ный ана­лиз ес­ли уро­вень за­ви­си­мо­сти па­ра­мет­ров обыч­но же­ст­ко детерминированных, мо­жет в ря­де слу­ча­ев при­ни­мать дру­гую фор­му.

Кор­ре­ля­ци­он­но-рег­рес­си­он­ный ана­лиз учи­ты­ва­ет меж­фак­тор­ные свя­зи, сле­до­ва­тель­но да­ет нам бо­лее пол­ное из­ме­ре­ние ро­ли ка­ж­до­го фак­то­ра: пря­мое, не­по­сред­ст­вен­ное его влия­ние на ре­зуль­та­тив­ный при­знак; кос­вен­ное влия­ние фак­то­ра че­рез влия­ние его на дру­гие фак­то­ры; влия­ние всех фак­то­ров на ре­зуль­та­тив­ный при­знак. Ес­ли связь ме­ж­ду фак­то­ра­ми не­су­ще­ст­вен­на, мож­но ог­ра­ни­чить­ся ин­декс­ным ана­ли­зом. В про­тив­ном слу­чае его по­лез­но до­пол­нить кор­ре­ля­ци­он­но-рег­рес­си­он­ным из­ме­ре­ни­ем влия­ния фак­то­ров, да­же ес­ли они функ­цио­наль­но свя­за­ны с ре­зуль­та­тив­ным при­зна­ком.

За­да­чи кор­ре­ля­ци­он­но-рег­рес­си­он­но­го ана­ли­за и мо­де­ли­ро­ва­ния

В со­от­вет­ст­вии с сущ­но­стью кор­ре­ля­ци­он­ной свя­зи ее изу­че­ние име­ет две це­ли: 1) из­ме­ре­ние па­ра­мет­ров урав­не­ния, вы­ра­жаю­ще­го связь сред­них ве­ли­чин за­ви­си­мой пе­ре­мен­ной со зна­че­ния­ми не­за­ви­си­мой пе­ре­мен­ной (за­ви­си­мость сред­них ве­ли­чин ре­зуль­та­тив­но­го при­зна­ка от зна­че­ний од­но­го или не­сколь­ких фак­тор­ных при­зна­ков); 2) из­ме­ре­ние тес­но­ты свя­зи двух (или боль­ше­го чис­ла) при­зна­ков ме­ж­ду со­бой. Вто­рая за­да­ча спе­ци­фич­на для ста­ти­сти­че­ских свя­зей, а пер­вая раз­ра­бо­та­на для функ­цио­наль­ных свя­зей и яв­ля­ет­ся об­щей. Ос­нов­ным ме­то­дом ре­ше­ния за­да­чи на­хо­ж­де­ния па­ра­мет­ров урав­не­ния свя­зи яв­ля­ет­ся ме­тод наи­мень­ших квад­ра­тов, раз­ра­бо­тан­ный К.Ф.Га­ус­сом. Он со­сто­ит в ми­ни­ми­за­ции сум­мы квад­ра­тов от­кло­не­ний фак­ти­че­ски из­ме­рен­ных зна­че­ний за­ви­си­мой пе­ре­мен­ной y от ее зна­че­ний, вы­чис­лен­ных по урав­не­нию свя­зи с фак­тор­ным при­зна­ком (мно­ги­ми при­зна­ка­ми) x.

Для из­ме­ре­ния тес­но­ты свя­зи при­ме­ня­ет­ся не­сколь­ко по­ка­за­те­лей. При пар­ной свя­зи тес­но­та свя­зи из­ме­ря­ет­ся пре­ж­де все­го кор­ре­ля­ци­он­ным от­но­ше­ни­ем. Квад­рат кор­ре­ля­ци­он­но­го от­но­ше­ния - это от­но­ше­ние меж­груп­по­вой дис­пер­сии ре­зуль­та­тив­но­го при­зна­ка, ко­то­рая вы­ра­жа­ет влия­ние раз­ли­чий груп­пи­ро­воч­но­го при­зна­ка на сред­нюю ве­ли­чи­ну ре­зуль­та­тив­но­го при­зна­ка, к об­щей дис­пер­сии ре­зуль­та­тив­но­го при­зна­ка, вы­ра­жаю­щей влия­ние на не­го всех при­чин и ус­ло­вий. Квад­рат кор­ре­ля­ци­он­но­го от­но­ше­ния на­зы­ва­ет­ся ко­эф­фи­ци­ен­том де­тер­ми­на­ции.

, где yj - ин­ди­ви­ду­аль­ные зна­че­ния ре­зуль­та­тив­но­го при­зна­ка, f - час­то­та в j-й груп­пе. Дан­ное урав­не­ние при­ме­ня­ет­ся при рас­че­те по­ка­за­те­ля тес­но­ты свя­зи по ана­ли­ти­че­ской груп­пи­ров­ке. Обыч­но же для рас­че­та кор­ре­ля­ци­он­но­го от­но­ше­ния по урав­не­нию свя­зи (урав­не­нию пар­ной и мно­же­ст­вен­ной рег­рес­сии) при­ме­ня­ет­ся фор­му­ла.

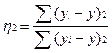. Сум­ма квад­ра­тов в чис­ли­те­ле - это объ­яс­нен­ная свя­зью с фак­то­ром x дис­пер­сия ре­зуль­та­тив­но­го при­зна­ка y. Она вы­чис­ля­ет­ся по ин­ди­ви­ду­аль­ным дан­ным, по­лу­чен­ным для ка­ж­дой еди­ни­цы со­во­куп­но­сти на ос­но­ве урав­не­ния рег­рес­сии.

Ес­ли урав­не­ние вы­бра­но не­вер­но или сде­ла­на ошиб­ка при рас­че­те его па­ра­мет­ров, то сум­ма квад­ра­тов в чис­ли­те­ле мо­жет ока­зать­ся боль­ше чем в зна­ме­на­те­ле, и от­но­ше­ние ут­ра­тит тот смысл, ко­то­рый долж­но иметь, а имен­но ка­ко­ва до­ля об­щей ва­риа­ции ре­зуль­та­тив­но­го при­зна­ка, объ­яс­ни­мая на ос­но­ве вы­бран­но­го урав­не­ния свя­зи его с фак­тор­ным при­зна­ком (при­зна­ка­ми). Что­бы из­бе­жать оши­боч­но­го ре­зуль­та­та, луч­ше вы­чис­лять кор­ре­ля­ци­он­ное от­но­ше­ние по дру­гой фор­му­ле:

, не столь на­гляд­но вы­яв­ляю­щий сущ­ность по­ка­за­те­ля, но за­то пол­но­стью га­ран­ти­рую­щий от воз­мож­но­го ис­ка­же­ния.

Dоб­щая=Dобъ­яс­нена урав­не­ни­ем рег­рес­сии +Dо­ста­точ­ная

Урав­не­ние кор­ре­ля­ци­он­ной свя­зи из­ме­ря­ет за­ви­си­мость ме­ж­ду ва­риа­ци­ей ре­зуль­та­тив­но­го при­зна­ка и ва­риа­ци­ей фак­тор­но­го при­зна­ка. Ме­ры тес­но­ты свя­зи из­ме­ря­ют до­лю ва­риа­ции ре­зуль­та­тив­но­го при­зна­ка, ко­то­рая свя­за­на кор­ре­ля­ци­он­но с ва­риа­ци­ей фак­тор­но­го при­зна­ка.

Ин­тер­пре­ти­ро­вать кор­ре­ля­ци­он­ные по­ка­за­те­ли стро­го сле­ду­ет лишь в тер­ми­нах ва­риа­ции (раз­ли­чий в про­стран­ст­ве) от­кло­не­ний от сред­ней ве­ли­чи­ны. Ес­ли же за­да­ча ис­сле­до­ва­ния со­сто­ит в из­ме­ре­нии свя­зи не ме­ж­ду ва­риа­ци­ей двух при­зна­ков в со­во­куп­но­сти, а ме­ж­ду из­ме­ре­ния­ми при­зна­ков объ­ек­та во вре­ме­ни, то ме­тод кор­ре­ля­циоо­но-рег­рес­си­он­но­го ана­ли­за тре­бу­ет зна­чи­тель­но­го из­ме­не­ния.

Из вы­ше­при­ве­ден­но­го оп­ре­де­ле­ния об ин­тер­пре­та­ции по­ка­за­те­лей кор­ре­ля­ции сле­ду­ет, что нель­зя трак­то­вать кор­ре­ля­цию при­зна­ков как связь их уров­ней. Это яс­но хо­тя бы из та­ко­го при­ме­ра: Ес­ли бы все сту­ден­ты, ко­то­рые хо­дят на лек­ции, учи­лись бы толь­ко на пя­тер­ки, то ва­риа­ция это­го при­зна­ка рав­ня­лась бы ну­лю, а сле­до­ва­тель­но ус­пе­вае­мость аб­со­лют­но не мог­ла бы вли­ять на по­се­щае­мость. Па­ра­мет­ры кор­ре­ля­ции ме­ж­ду ус­пе­вае­мо­стью и по­се­щае­мо­стью все­гда бу­дут рав­нять­ся ну­лю. Но ведь и в этом слу­чае уро­вень зна­ний за­ви­сел бы от чис­ла лек­ций - он был бы тем вы­ше, чем боль­ше лек­ций.

Итак, стро­го го­во­ря, ме­тод кор­ре­ля­циоо­но-рег­рес­си­он­но­го ана­ли­за не мо­жет объ­яс­нить ро­ли фак­тор­ных при­зна­ков в соз­да­нии ре­зуль­та­тив­но­го при­зна­ка. Это очень серь­ез­ное ог­ра­ни­че­ние ме­то­да, о ко­то­ром не сле­ду­ет за­бы­вать.

Сле­дую­щий об­щий во­прос - это во­прос о “чис­то­те” из­ме­ре­ния влия­ния ка­ж­до­го при­зна­ка. Груп­пи­ров­ка со­во­куп­но­сти по од­но­му фак­тор­но­му при­зна­ку мо­жет от­ра­зить влия­ние имен­но дан­но­го при­зна­ка на ре­зуль­та­тив­ный при­знак при ус­ло­вии, что все дру­гие фак­то­ры не свя­за­ны с изу­чае­мым, а слу­чай­ные от­кло­не­ния и ошиб­ки взаи­мо­по­га­си­лись в боль­шой со­во­куп­но­сти. Ес­ли же изу­чае­мый фак­тор свя­зан с дру­ги­ми фак­то­ра­ми, влияю­щи­ми на ре­зуль­та­тив­ный при­знак, бу­дет по­лу­че­на не “чис­тая” ха­рак­те­ри­сти­ка влия­ния толь­ко од­но­го фак­то­ра, а слож­ный ком­плекс, со­стоя­щий как из не­по­сред­ст­вен­но­го влия­ния фак­то­ра, так и из его кос­вен­ных влия­ний, че­рез его связь с дру­ги­ми фак­то­ра­ми и их влия­ние на ре­зуль­та­тив­ный при­знак. Дан­ное по­ло­же­ние пол­но­стью от­но­сит­ся и к пар­ной кор­ре­ля­ци­он­ной свя­зи. Главным достоинством корреляционно-регрессионного метода заключается в возможности разделить влияние комплекса факторных признаков, анализировать различные стороны сложной системы взаимосвязей. Кор­ре­ля­ци­он­ный ме­тод при объ­е­ме со­во­куп­но­сти око­ло 100 еди­ниц по­зво­ля­ет вес­ти ана­лиз сис­те­мы с 8-10 фак­то­ра­ми и раз­де­лить их влия­ние.

Не­об­хо­ди­мо ска­зать и о дру­гих за­да­чах при­ме­не­ния ме­то­да, имею­щих не фор­маль­но ма­те­ма­ти­че­ских, а со­дер­жа­тель­ный ха­рак­тер.

1. За­да­ча вы­де­ле­ния важ­ней­ших фак­то­ров, влияю­щих на ре­зуль­та­тив­ный при­знак (т.е. на ва­риа­цию его зна­че­ний в со­во­куп­но­сти). Эта за­да­ча ре­ша­ет­ся в ос­нов­ном на ба­зе мер тес­но­ты свя­зи фак­то­ров с ре­зуль­та­тив­ным при­зна­ком.

2. За­да­ча про­гно­зи­ро­ва­ния воз­мож­ных зна­че­ний ре­зуль­та­тив­но­го при­зна­ка при за­да­вае­мых зна­че­ни­ях фак­тор­ных при­зна­ков. Та­кая за­да­ча ре­ша­ет­ся пу­тем под­ста­нов­ки ожи­дае­мых, или пла­ни­руе­мых, или воз­мож­ных зна­че­ний фак­тор­ных при­зна­ков в урав­не­ние свя­зи и вы­чис­ле­ния ожи­дае­мых зна­че­ний ре­зуль­та­тив­но­го при­зна­ка. При­хо­дит­ся ре­шать и об­рат­ную за­да­чу: вы­чис­ле­ние не­об­хо­ди­мых зна­че­ний фак­тор­ных при­зна­ков для обес­пе­че­ния пла­но­во­го или же­лае­мо­го зна­че­ния ре­зуль­та­тив­но­го при­зна­ка. Эта за­да­ча обыч­но не име­ет од­но­го ре­ше­ния.

При ре­ше­нии ка­ж­дой из на­зван­ных за­дач нуж­но учи­ты­вать осо­бен­но­сти и ог­ра­ни­че­ния кор­ре­ля­ци­он­но­го ме­то­да. Вся­кий раз не­об­хо­ди­мо спе­ци­аль­но обос­но­вы­вать воз­мож­ность при­чин­ной ин­тер­пре­та­ции урав­не­ния как объ­яс­няю­ще­го связь ме­ж­ду ва­риа­ци­ей фак­то­ра и ре­зуль­та­та. Труд­но обес­пе­чить раз­дель­ную оцен­ку влия­ния ка­ж­до­го из фак­то­ров. В этом от­но­ше­нии кор­ре­ля­ци­он­ные ме­то­ды глу­бо­ко про­ти­во­ре­чи­вы. С од­ной сто­ро­ны, их иде­ал - из­ме­ре­ния чис­то­го влия­ния ка­ж­до­го фак­то­ра. С дру­гой сто­ро­ны, та­кое из­ме­ре­ние воз­мож­но при от­сут­ст­вии свя­зи ме­ж­ду фак­то­ра­ми и слу­чай­ной ва­риа­ции при­зна­ков. А то­гда связь яв­ля­ет­ся функ­цио­наль­ной, и кор­ре­ля­ци­он­ные ме­то­ды ана­ли­за из­лиш­ни. В ре­аль­ных сис­те­мах связь все­гда име­ет ста­ти­сти­че­ский ха­рак­тер, и то­гда иде­ал ме­то­дов кор­ре­ля­ции ста­но­вит­ся не­дос­ти­жи­мым. Но это не зна­чит, что по­доб­ные ме­то­ды не нуж­ны. Это оз­на­ча­ет не­дос­ти­жи­мость аб­со­лют­ной ис­ти­ны в по­зна­нии ре­аль­ных свя­зей. Вся­кая на­уч­ная ис­ти­на - от­но­си­тель­на.

Вы­чис­ле­ние и ин­тер­пре­та­ция па­ра­мет­ров

пар­ной ли­ней­ной кор­ре­ля­ции

Про­стей­шей сис­те­мой кор­ре­ля­ци­он­ной свя­зи яв­ля­ет­ся ли­ней­ная связь ме­ж­ду дву­мя при­зна­ка­ми - пар­ная ли­ней­ная кор­ре­ля­ция. Прак­ти­че­ское ее зна­че­ние в том, что есть сис­те­мы, в ко­то­рых сре­ди всех фак­то­ров, влияю­щих на ре­зуль­та­тив­ный при­знак, вы­де­ля­ет­ся один важ­ней­ший фак­тор, ко­то­рый в ос­нов­ном оп­ре­де­ля­ет ва­риа­цию ре­зуль­та­тив­но­го при­зна­ка. Из­ме­ре­ние пар­ных кор­ре­ля­ций со­став­ля­ет не­об­хо­ди­мый этап в изу­че­нии слож­ных, мно­го­фак­тор­ных свя­зей. Есть та­кие сис­те­мы свя­зей, при изу­че­нии ко­то­рых не­об­хо­ди­мо пред­по­честь пар­ную кор­ре­ля­цию.

Из­ме­ре­ние свя­зи не­ко­ли­че­ст­вен­ных па­ра­мет­ров.

Кор­ре­ля­ци­он­но-рег­рес­си­он­ный ме­тод при­ме­ним толь­ко к ко­ли­че­ст­вен­ным при­зна­кам. Од­на­ко за­да­ча из­ме­ре­ния свя­зи ста­вит­ся пе­ред ста­ти­сти­кой и по от­но­ше­нию к та­ким при­зна­кам как пол, се­мей­ное по­ло­же­ние, т.е. при­зна­кам не имею­щим ко­ли­че­ст­вен­но­го вы­ра­же­ния.

Уче­ны­ми ря­да стран за по­след­ние 100 лет раз­ра­бо­та­но не­сколь­ко ме­то­дов из­ме­ре­ния свя­зи та­ких при­зна­ков. Опи­са­тель­ные при­зна­ки - обыч­но аль­тер­на­тив­ные при­зна­ки, при ко­то­рых ка­ж­дый име­ет по две раз­но­вид­но­сти. На­при­мер, боль­ные мо­гут вы­здо­ро­веть, а мо­гут не вы­здо­ро­веть, при­знак есть (нет). В тех слу­ча­ях, ко­гда на­хо­дя­щие­ся в свя­зи яв­ле­ния пред­став­ле­ны опи­са­тель­ны­ми ве­ли­чи­на­ми, ко­эф­фи­ци­ент кор­ре­ля­ции на­хо­дят по сле­дую­щей фор­му­ле.

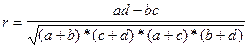, где a,b,c,d - ко­ли­че­ст­во слу­ча­ев от­дель­ных ком­би­на­ций раз­но­вид­но­стей ис­сле­дуе­мых яв­ле­ний.

При вы­чис­ле­нии ко­эф­фи­ци­ен­та кор­ре­ля­ции зна­ме­на­тель фор­му­лы все­гда име­ет по­ло­жи­тель­ный знак. Знак пе­ред r за­ви­сит от то­го, ка­кое из про­из­ве­де­ний боль­ше ad или bc. Для то­го, что­бы лег­че вы­чис­лить ко­эф­фи­ци­ент кор­ре­ля­ции поль­зу­ют­ся так на­зы­вае­мой че­ты­рех­поль­ной таб­ли­цей. В пер­вом столб­це этой таб­ли­це на­но­сят обе раз­но­вид­но­сти од­но­го яв­ле­ния - Х1 и Х2, а в пер­вой стро­ке - обе раз­но­вид­но­сти вто­ро­го -Y1 и Y2. При этом X1 и Y2 обо­зна­ча­ют по­ло­жи­тель­ные раз­но­вид­но­сти, а X2 и Y1 - от­ри­ца­тель­ные. В ука­зан­ных вы­ше при­ме­рах под по­ло­жи­тель­ны­ми раз­но­вид­но­стя­ми под­ра­зу­ме­ва­ют вы­здо­ро­вев­ших, по­лу­чив­ших от­рав­ле­ние. При та­ком со­стоя­нии че­ты­рех­поль­ная таб­ли­ца при­ни­ма­ет сле­дую­щий вид:

X	Y1	Y2	Все­го
X1	a	b	(a+b)
X2	c	d	(c+d)
Все­го	(a+c)	(b+d)	(a+b+c+d)

При­мер 1. Име­ют­ся сле­дую­щие дан­ные о вак­ци­на­ции про­тив грип­па и за­бо­ле­вае­мо­сти грип­пом во вре­мя эпи­де­мии:

X	Y1 За­бо­ле­ло	Y2 Не за­бо­ле­ло	Все­го
X1 Вак­ци­ни­ро­ва­но	a	b	(a+b)
X2 Не вакцинировано	c	d	(c+d)
Все­го	(a+c)	(b+d)	(a+b+c+d)

Тре­бу­ет­ся оп­ре­де­лить раз­мер свя­зи ме­ж­ду про­ве­ден­ной вак­ци­на­ци­ей и за­бо­ле­вае­мо­стью.

r=-0.6.

Ко­эф­фи­ци­ент кор­ре­ля­ции по­ка­зы­ва­ет об­рат­ную связь: вак­ци­ни­ро­ван­ные ре­же бо­ле­ют, чем не вакцинированные.

Не­за­ви­си­мо то то­го, что ка­ж­дый из опи­са­тель­ных при­зна­ков, не­смот­ря на раз­ни­цу в чис­лен­но­сти его раз­но­вид­но­стей, мож­но све­сти к аль­тер­на­тив­но­му - толь­ко с дву­мя раз­но­вид­но­стя­ми, до­воль­но час­то в прак­ти­ке в воз­ни­ка­ет не­об­хо­ди­мость ра­бо­тать с опи­са­тель­ны­ми при­зна­ка­ми бо­лее двух раз­но­вид­но­стей. В та­ких слу­ча­ях не­об­хо­ди­мо при вы­чис­ле­нии ко­эф­фи­ци­ен­та кор­ре­ля­ции со­став­лять так на­зы­вае­мую кор­ре­ля­ци­он­ную таб­ли­цу (где X1,X2,...Xn - обо­зна­ча­ют раз­но­вид­ность од­но­го при­зна­ка, а Y1, Y2... Yn - раз­но­вид­но­сти дру­го­го).

При на­ли­чии та­кой схе­мы ко­эф­фи­ци­ент кор­ре­ля­ции на­хо­дят по фор­му­ле: , где (2 - ко­эф­фи­ци­ент свя­зи, m- чис­ло раз­но­вид­но­стей яв­ле­ния Х; n - чис­ло раз­но­вид­но­стей яв­ле­ния Y.

При­мер 2. Оп­ро­ше­ны жи­те­ли 130 на­се­лен­ных пунк­тов в от­но­ше­нии жи­лищ­ных и бы­то­вых ус­ло­вий и о за­бо­ле­вае­мо­сти ту­бер­ку­ле­зом.

	От­сут­ст­ву­ет Y1	Низ­кая Y2	Сред­няя Y3	Вы­со­кая Y4	Ито­го	Ча­ст­ное
Пло­хие X1	-	(100) 2.5	(100) 2.5	(400) 20		0.625
Сред­ние X2	(25) 0.833	(25) 0.65	(400) 10	-	11.5	0.382
Хо­ро­шие X3	(25) 0.833	(400) 10	(25) 0.65	-	11.5	0.382
От­лич­ные X4	(400) 13.3	(25) 0.65	(25) 0.65	-	14.58	0.486
Ито­го...						1.875

Вы­чис­ле­ние ко­эф­фи­ци­ен­та кор­ре­ля­ции про­хо­дит че­рез сле­дую­щие эта­пы ра­бо­ты:

1. Ка­ж­дую из на­блю­дае­мых час­тот от­дель­ных ком­би­на­ций раз­но­вид­но­стей на­блю­дае­мых при­зна­ков воз­во­дят в квад­рат.

2. По­лу­чен­ные квад­ра­ты де­лят на сум­мы всех час­тот со­от­вет­ст­вую­ще­го столб­ца

3. Скла­ды­ва­ют по­лу­чен­ные ча­ст­ные ка­ж­дой стро­ки

4. По­лу­чен­ные та­ким об­ра­зом час­то­ты де­лят на об­щее ко­ли­че­ст­во со­от­вет­ст­вую­щей раз­но­вид­но­сти при­зна­ка Х.

5. По­лу­чен­ные ча­ст­ные скла­ды­ва­ют

6. На­хо­дят ко­эф­фи­ци­ент (2, вы­чи­тая из ито­га еди­ни­цу;

7. На­хо­дят (2 ко­эф­фи­ци­ент свя­зи =0.875-(4-1)(4-1)/130=0.806

8. На­хо­дят ко­эф­фи­ци­ент кор­ре­ля­ции. В на­шем слу­чае ко­эф­фи­ци­ент кор­ре­ля­ции ра­вен 0.77, что ука­зы­ва­ет на до­воль­но тес­ную связь ме­ж­ду изу­чае­мы­ми яв­ле­ния­ми.

Данный метод пригоден также и для экспрессной оценки связи между количественными (например, возраст) и качественными (например, брак) параметрами.

Конечно, расчет параметров на основе группировки является приближенным: реальные значения признаков заменяются серединами интервалов. Не учитывается неравномерность изменения частот внутри интервалов. Казалось бы с появлением ЭВМ этот метод должен отмереть. Однако для больших совокупностей в десятки и сотни тысяч единиц большинство программ ввиду ограничений на объем оперативной памяти непригодно. Да и сам процесс занесения в память ЭВМ сотни тысяч чисел занял бы столь громадное время, что выигрыш во времени расчета на ЭВМ был бы многократно превышен. Таким образом, иногда трудоемкость расчета с помощью группировки и простого калькулятора оказывается намного меньше, чем с помощью ЭВМ, а степень точности достаточна для большинства задач анализа связи.

В слу­чае, ко­гда па­ра­мет­ры из­ме­ря­ют­ся ко­ли­че­ст­вен­но, тес­но­та пар­ной ли­ней­ной кор­ре­ля­ци­он­ной свя­зи мо­жет быть из­ме­ре­на кор­ре­ля­ци­он­ным от­но­ше­ни­ем h:

.

Кро­ме то­го, при ли­ней­ной фор­ме урав­не­ния при­ме­ня­ет­ся и дру­гой по­ка­за­тель тес­но­ты свя­зи - ко­эф­фи­ци­ент кор­ре­ля­ции rxy. Этот по­ка­за­тель пред­став­ля­ет со­бой стан­дар­ти­зо­ван­ный ко­эф­фи­ци­ент рег­рес­сии, т.е. ко­эф­фи­ци­ент вы­ра­жен­ный не в аб­со­лют­ных еди­ни­цах из­ме­ре­ния при­зна­ков, а в до­лях сред­не­го квад­ра­ти­че­ско­го от­кло­не­ния ре­зуль­ти­рую­ще­го при­зна­ка:

Ко­эф­фи­ци­ент кор­ре­ля­ции был пред­ло­жен анг­лий­ским ста­ти­сти­ком Пирсоном. Его ин­тер­пре­та­ция та­ко­ва: от­кло­не­ние при­зна­ка-фак­то­ра от его сред­не­го зна­че­ния на ве­ли­чи­ну сво­его сред­не­го квад­ра­тич­но­го от­кло­не­ния в сред­нем по со­во­куп­но­сти при­во­дит к от­кло­не­нию при­зна­ка-ре­зуль­та­та от сво­его сред­не­го зна­че­ния на Rxy его сред­не­го квад­ра­тич­но­го от­кло­не­ния. В от­ли­чие от ко­эф­фи­ци­ен­та регрессии b ко­эф­фи­ци­ент кор­ре­ля­ции не за­ви­сит от при­ня­тых еди­ниц из­ме­ре­ния па­ра­мет­ров, а ста­ло быть он срав­ним для лю­бых при­зна­ков.

Для ин­тер­пре­та­ции ко­эф­фи­ци­ен­та кор­ре­ля­ции не­об­хо­ди­мо знать об­ласть его су­ще­ст­во­ва­ния 0£|r|£1. Как яс­но из фор­му­лы, ми­ни­маль­ное, имен­но ну­ле­вое зна­че­ние ко­эф­фи­ци­ен­та кор­ре­ля­ции мо­жет быть дос­тиг­ну­то, ес­ли по­ло­жи­тель­ные и от­ри­ца­тель­ные про­из­ве­де­ния от­кло­не­ний при­зна­ков от их сред­них ве­ли­чин в чис­ли­те­ле урав­но­ве­сят друг дру­га. Это сви­де­тель­ст­во­ва­ло бы о пол­ном от­сут­ст­вии свя­зи, но ве­ро­ят­ность та­ко­го аб­со­лют­но точ­но­го взаи­мо­по­га­ше­ния аб­со­лют­но ма­ла для лю­бой ре­аль­ной, но бес­ко­неч­но боль­шой со­во­куп­но­сти. По­это­му и при от­сут­ст­вии ре­аль­ной свя­зи ко­эф­фи­ци­ент кор­ре­ля­ции на прак­ти­ке не ра­вен 0.

Мак­си­маль­но тес­ная связь - это связь функ­цио­наль­ная, ко­гда ка­ж­дое ин­ди­ви­ду­аль­ное зна­че­ние ре­зуль­та­тив­но­го при­зна­ка мо­жет быть од­но­знач­но по­став­ле­но в со­от­вет­ст­вие к фак­то­ру (на­при­мер, y=cx, где с - кон­стан­та).

Дата добавления: 2014-01-05