Определение моды и медианы в дискретном вариационном ряду

Пример 7: По данным табл. 5.7 определите модальное и медианное значения тарифного разряда.

Таблица 5.7

Распределение рабочих предприятия по тарифному разряду

Тарифный разряд, x	Численность рабочих, чел., f
Мо = 5	60 – наибольшая частота
Всего:

Мо = 5, так как f = 60 – наибольшая частота.

Для определения медианного значения признака по следующей формуле находят порядковый номер медианной единицы ряда:

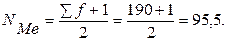
Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95-м и 96-м рабочими. Определим, какой тарифный разряд имеют рабочие с этими порядковыми номерами.

Второй тарифный разряд имеют рабочие с порядковыми номерами с 1 по 12;

третий – с 13 по 12+48=60;

четвертый – с 61 по 60+56=116.

Следовательно, рабочие с порядковыми номерами 95 и 96 имеют четвертый тарифный разряд: Ме = 4.

2) Определение моды и медианы в интервальном ряду требует проведения определенных расчетов на основе следующих формул:

,

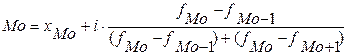где 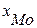– нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);

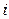– длина модального интервала;

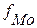– частота модального интервала;

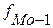– частота интервала, предшествующего модальному;

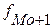– частота интервала, следующего за модальным.

,

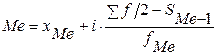где 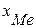– нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого равна или превышает полусумму всех частот ряда);

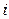– длина медианного интервала;

– частота медианного интервала;

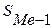– накопленная частота интервала, предшествующего медианному.

Пример 8: По данным табл. 5.8 определите модальное и медианное значения стоимости основных производственных фондов (ОПФ).

Таблица 5.8

Распределение малых предприятий региона по стоимости

основных производственных фондов (ОПФ) в 1996 г.

Группы предприятий по стоимости ОПФ, млн руб. x	14–16	16–18	18–20	20–22	22–24	Итого
Число предприятий, ед. f
Накопленная частота, ед. S						х

Так как f =10 – наибольшая частота, то интервал (18–20) модальный.

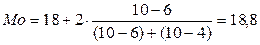млн руб.

Большинство малых предприятий региона имеют стоимость ОПФ, равную 18,8 млн руб.

S = 18 > значит (18–20) – медианный интервал.

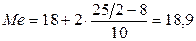млн руб.

Половина малых предприятий региона имеют стоимость ОПФ меньше 18,9 млн руб., а половина – больше этого значения.

Аналогично с нахождением медианы в вариационных рядах распределения можно отыскать значения признака у единиц, делящих ряд на 4, 10, 100 равных частей. Эти величины называются соответственно «квартили», «децили» и «перцентили».

Децили

d₁ d₂ Me d₉

Q₁ Q₃

Р а н ж и р о в а н н а я с о в о к у п н о с т ь

Медиана

Квартили

Рис. 1. Расположение структурных средних в статистической совокупности

Квартили – значения признака, делящие ранжированную совокупность на 4 равные части (на рис. 1 это точки Q₁, Me и Q₃).

, ,

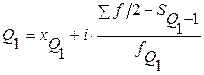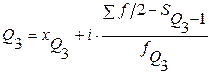где 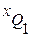– нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);

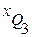– нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);

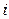– длина интервала;

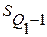– накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;

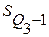– накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;

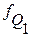– частота интервала, содержащего нижний квартиль;

– частота интервала, содержащего верхний квартиль.

Децилем называется структурная переменная, которая делит распределение на 10 равных частей по 10% единиц в каждой части. Децилей – девять, децильных групп – десять.

Децили вычисляются по той же схеме:

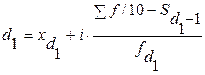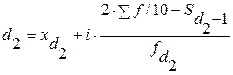, и т. д.

Анализ вариационного ряда дополняется расчетом показателя дифференциации.

По ряду распределения определяется коэффициент децильной дифференциации:

.

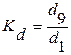Он показывает, во сколько раз наименьший уровень признака из 10% единиц, имеющих наибольший уровень признака, больше наибольшего уровня признака, из 10% единиц совокупности, имеющих наименьший уровень признака. Применяется для характеристики дифференциации населения по уровню дохода.

По первичным данным определяется коэффициент фондовой дифференциации:

,

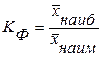где 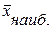– среднее значение признака в 10-й децильной группе;

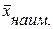– среднее значение признака в 1-й децильной группе.

Дата добавления: 2014-01-05