Абсолютные и средние показатели вариации. Вариация – различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период

Показатели вариации

Вариация – различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период, момент времени.

Показатели вариации – это показатели отклонений индивидуальных значений признака от их среднего значения. Чем меньше эти отклонения, тем средняя более показательна, надежна.

1. Размах вариации показывает разность между наибольшим () и наименьшим () значениями варьирующего признака:

2. Среднее линейное отклонение вычисляется как средняя арифметическая из абсолютных значений отклонений вариантов признака от их среднего значения .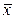

– простое среднее линейное отклонение;

– взвешенное среднее линейное отклонение.

Разности в числителе взяты по модулю, иначе среднее линейное отклонение всегда будет равно 0 (так как сумма всех отклонений отдельных вариантов признака от их среднего значения равна нулю: ).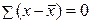

На практике среднее линейное отклонение используют редко, только в тех случаях, когда суммирование показателей без учета знака имеет экономический смысл.

3. Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

– простая дисперсия;

– взвешенная дисперсия.

4. Среднее квадратическое отклонение равно корню квадратному из дисперсии:

– простое среднее квадратическое отклонение;

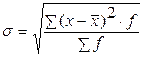– взвешенное среднее квадратическое отклонение.

Среднее линейное отклонение и среднее квадратическое отклонение показывают, на сколько в среднем отклоняются конкретные варианты признака от их среднего значения, выражаются в тех же единицах измерения, что и признак.

Среднее квадратическое отклонение показывает абсолютную меру колеблемости признака в совокупности.

Дата добавления: 2014-01-05