Система средних показателей ряда динамики

1. Средний уровень ряда динамики:

а) в интервальных рядах:

· с равными интервалами:

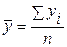(формула средней арифметической простой);

· с неравными интервалами:

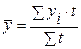(формула средней арифметической взвешенной),

где t – периоды времени;

б) в моментных рядах:

· с равноотстоящими уровнями:

(формула средней хронологической простой),

где – уровни ряда,

n – число уровней;

· с неравноотстоящими уровнями:

(формула средней хронологической взвешенной),

где n– 1- число промежутков времени между уровнями.

2. Средний абсолютный прирост. Показывает, на сколько в среднем в единицу времени изменяется уровень динамического ряда.

,

где n – 1 – число цепных абсолютных приростов.

Используя взаимосвязь цепных и базисных абсолютных приростов, получаем:

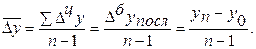
3. Средний темп роста. Показывает, во сколько раз в среднем в единицу времени увеличивается уровень динамического ряда.

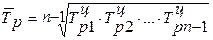(формула средней геометрической),

где n – 1 – число цепных темпов роста.

Используя взаимосвязь цепных и базисных темпов роста, можно получить следующую формулу для вычисления среднего темпа роста:

,

где n – число уровней ряда динамики.

4. Средний темп прироста. Показывает, на сколько процентов в среднем в единицу времени изменяется уровень динамического ряда.

.

Пример 1. Имеются следующие данные об объеме пассажирооборота железнодорожного транспорта.

Таблица 6.2

Динамика пассажирооборота железнодорожного транспорта

Год	Пассажиро-оборот, млн пасс.-км	Цепные показатели динамики
Абсолютный прирост, млн пасс.-км	Темп роста, %	Темп прироста, %	Абсолютное значение одного процента прироста, млн пасс.-км
		–	–	–	–
		–7
			99,4
				7,8	24,23

(По данным статистических сборников «Кировская область в 2005 году». Ч. 2. С. 113.)

Вычислить и проставить в таблицу уровни ряда динамики и недостающие показатели динамики.

Решение:

1. Введем в таблице обозначения:

t – год (1 графа);

y – пассажирооборот (2 графа);

– цепной абсолютный прирост;

– цепной темп роста;

– цепной темп прироста;

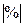– абсолютное значение одного процента прироста.

Год t	Пассажиро-оборот, млн пасс.-км y	Цепные показатели динамики
Абсолютный прирост, млн пасс.-км	Темп роста, %	Темп прироста, %	Абсолютное значение одного процента прироста, млн пасс.-км

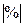
2. Определим по данным задачи уровни ряда динамики (у):

а) уровень 2001 г. определяем из формулы цепного абсолютного прироста:

;

;

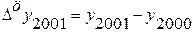млн пасс.-км;

б) уровень 2002 г. определим по формуле цепного темпа роста следующим образом:

;

;

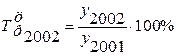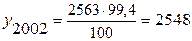млн пасс.-км;

в) уровень 2004 г. определим по формуле абсолютного значения 1% прироста:

;

;

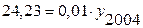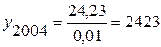млн пасс.-км;

г) уровень 2005 г. определим по формуле цепного темпа прироста следующим образом:

;

;

.

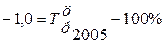Зная цепной темп роста 2005 года можно определить уровень ряда 2005 г.:

млн пасс.-км.

3. Определим цепные показатели динамики:

а) цепные абсолютные приросты находим как разность уровня ряда текущего периода и предыдущего. Например, абсолютный прирост 2002 г. определяем по формуле:

млн пасс.-км.

Остальные абсолютные приросты определяем по аналогии (табл. 6.3);

б) цепные темпы роста находим как отношение уровня ряда текущего периода к предыдущему. Например, темп роста 2001 г. равен:

.

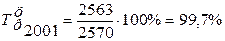Остальные темпы роста определяем по аналогии (табл. 6.3);

в) для определения темпа прироста нужно из соответствующего темпа роста вычесть 100%. Например,

г) абсолютное значение одного процента прироста – это одна сотая от предыдущего уровня ряда. Например, млн пасс.-км.

4. Представим исходные и расчетные значения в таблице.

Таблица 6.3

Динамика пассажирооборота железнодорожного транспорта

Год	Пассажиро-оборот, млн пасс.-км	Цепные показатели динамики
Абсолютный прирост, млн пасс.-км	Темп роста, %	Темп прироста, %	Абсолютное значение одного процента прироста, млн пасс.-км
		–	–	–	–
		–7	99,7	–0,3	25,70
		–15	99,4	–0,6	25,63
		-76	97,0	–3,0	25,48
		-49	98,0	–2,0	24,72
		–24	99,0	–1,0	24,23

Пример 2. По данным табл. 6.3 определить средние показатели ряда динамики: средний уровень ряда, средний абсолютный прирост, средний темп роста и средний темп прироста. Сделать выводы по результатам расчета.

Решение:

1. Определим средний уровень ряда динамики. Так как ряд интервальный (год – это интервал времени), с равными интервалами, то средний уровень ряда определяем по формуле средней арифметической простой:

млн пасс.-км., таким образом, среднегодовой пассажирооборот железнодорожного транспорта в 2000–2005 гг. составлял 2496 млн пасс.-км.

2. Определим средний абсолютный прирост по следующей формуле:

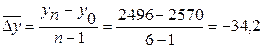млн пасс.-км., таким образом, за период 2000–2005 гг. среднем за год пассажирооборот железнодорожного транспорта снижался на 34,2 млн пасс.-км.

3. Определим средние темп роста и прироста:

;

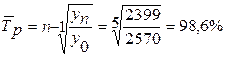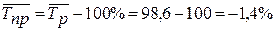, т. е. в среднем за год за период с 2000 по 2005 гг. пассажирооборот железнодорожного транспорта снижался на 1,4%.

Пример 3. Имеются следующие данные об изменении в списочном составе работников предприятия за январь, чел:

состояло по списку на 1 января 100;

уволено с 10 января 5;

зачислено с 20 января 2;

уволено с 25 января 3;

зачислено с 28 января 1.

Определите среднюю списочную численность работников предприятия за январь.

Решение:

Представим исходные данные задачи в виде интервального ряда динамики:

Период, дней t	Списочная численность, чел. y
10 – 1 = 9
20 – 10 = 10	100 – 5 = 95
25 – 20 = 5	95 + 2 = 97
28 – 25 = 3	97 – 3 = 94
31 – 28 + 1 = 4	94 + 1 = 95

Определим среднюю списочную численность работников за январь по формуле среднего уровня ряда динамики. Ряд динамики интервальный, с неравными интервалами. Средний уровень такого ряда определяется по формуле средней арифметической взвешенной:

человек.

Среднесписочная численность работников предприятия за январь составила 97 человек.

Кроме разобранных примеров решения задач полезным будет вспомнить решение задачи на определение цепных и базисных относительных показателей динамики (ОПД) в теме 4 «Статистические показатели. Абсолютные и относительные показатели», задачи на определение среднего остатка товаров за I квартал по формуле средней хронологической простой в теме 5 «Средние величины и показатели вариации» и задачи на определение среднего темпа роста по формуле средней геометрической простой в теме 5 «Средние величины и показатели вариации».

Дата добавления: 2014-01-05