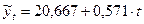КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Экстраполяция и интерполяция в динамических рядах
|
|
|
|
Метод скользящей средней. Объединяется определенное число, обычно нечетное, первых по порядку уровней ряда. Затем такое же число уровней начиная со второго, затем начиная с третьего и так далее. Рассчитываются средние величины, на основании которых судят о тенденции развития. Если объединяется нечетное число уровней, то среднее значение записывается году, находящемуся по середине. Если объединяется четное число уровней, то применяется так называемый способ центрирования.
Методы выявления основной тенденции развития явления во времени
Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Для выявления основной тенденции развития используются следующие методы:
Метод укрупнения периодов времени. Объединяются несколько уровней ряда, затем рассчитываются средние величины, на основании которых судят о тенденции развития.
Пример 4. Дан динамический ряд товарооборота за несколько лет.
Таблица 6.4
Динамика товарооборота фирмы
| Годы | Товарооборот, млн. руб. | Метод укрупнения периодов, млн. руб. | Трехлетние скользящие средние, млн. руб. | Четырехлетние скользящие средние (нецентрирован-ные) | Четырехлетние скользящие средние (центрирован-ные) | ||
 - -
| 
| - | |||||
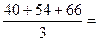 53 53
|  53 53
| 
| - | ||||
 56 56
| 
| (52,0+56,0):2=54 | |||||
 57 57
| 
| 56,75 | |||||
  55 55
| 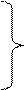
| 58,00 | |||||
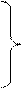
| 60,25 | ||||||
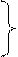 64 64
|
| 65,50 | |||||
| - | |||||||
| - | - |
Поскольку каждое следующее среднее значение больше предыдущего, то можно сделать вывод, что в данном ряде динамики тенденция к росту.
Метод аналитического выравнивания. Состоит в выражении тенденции с помощью математического уравнения:
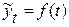 ,
,
где 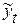 – уровни РД, вычисленные по аналитическому уравнению на момент времени t.
– уровни РД, вычисленные по аналитическому уравнению на момент времени t.
Простейшими моделями являются:
линейная функция: 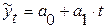 ,
,
где 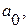
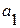 - параметры уравнения;
- параметры уравнения;
t – порядковый номер периода;
парабола: 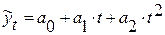 ,
,
экспонента: 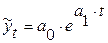 .
.
Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные цепные абсолютные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
Параболическая зависимость используется, если цепные абсолютные приросты сами по себе обнаруживают некоторую тенденцию развития, но цепные абсолютные приросты цепных абсолютных приростов (разности второго порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т. п.).
Выравнивание может производиться по среднему темпу роста, среднему абсолютному приросту, но наиболее точным является выравнивание методом наименьших квадратов, при котором находят такие параметры 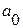 и
и 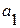 ,
, 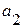 и т. д., чтобы выполнялось условие: сумма квадратов отклонений эмпирических (фактических) уровней от теоретических должна быть минимальной:
и т. д., чтобы выполнялось условие: сумма квадратов отклонений эмпирических (фактических) уровней от теоретических должна быть минимальной:
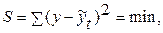 (1)
(1)
где y – уровни ряда;
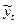 – выровненные значения.
– выровненные значения.
Для линейной модели 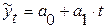 функция S =
функция S =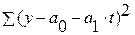 – это функция второго порядка от двух неизвестных
– это функция второго порядка от двух неизвестных 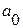 и
и 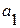 . Свое наименьшее значение она принимает в точке, где частные производные по параметрам
. Свое наименьшее значение она принимает в точке, где частные производные по параметрам 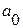 и
и 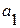 равны нулю. Согласно этому условие метода наименьших квадратов (1) можно преобразовать и получить следующую систему нормальных уравнений:
равны нулю. Согласно этому условие метода наименьших квадратов (1) можно преобразовать и получить следующую систему нормальных уравнений:
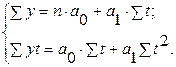
Если 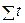 =0, то из последней системы получаем:
=0, то из последней системы получаем:
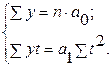 Откуда,
Откуда, 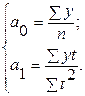
Как сделать, чтобы сумма номеров периодов ровнялась нулю (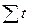 = 0)? Возможны два случая:
= 0)? Возможны два случая:
число уровней РД нечетное, тогда будем поступать следующим образом: пусть ряд динамики включает произвольные 5 лет:
| число уровней РД четное, тогда будем поступать следующим образом: пусть ряд динамики включает произвольные 6 лет:
|
Рассмотрим технику выравнивания ряда динамики по прямой линии на примере.
Таблица 6.5
Расчетная таблица
| Годы | Товарооборот, млн. руб. | Номер года, t | 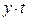
| 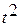
| 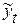
| 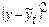
|
| -5 -3 -1 | -80 -54 -25 | 17,81 18,95 20,10 21,24 22,38 23,52 | 3,276 0,903 24,01 1,538 0,384 2,310 | |||
| всего | 124,00 | 32,421 |
Расчетные значения из таблицы 1 подставляем в систему нормальных уравнений:
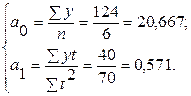
Получили следующее уравнение прямой:
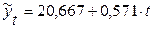 .
.
По уравнению прямой находим выровненные значения 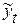 :
:
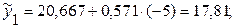
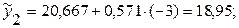
…
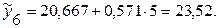
Для выровненных и исходных уровней должно всегда выполняться условие:
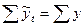 (124 = 124,00).
(124 = 124,00).
Изобразим графически исходные уровни РД и уравнение найденной прямой:
| |||
 |
Т.к. 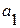 > 0, то в РД тенденция к росту (товарооборот фирмы за период с 1995 по 2000 гг. в целом увеличивается).
> 0, то в РД тенденция к росту (товарооборот фирмы за период с 1995 по 2000 гг. в целом увеличивается).
Система нормальных уравнений для параболы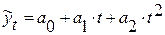 , если
, если 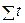 =0:
=0:
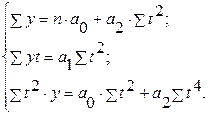
Система нормальных уравнений для экспоненты 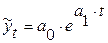 , если
, если 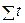 =0:
=0:
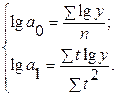
Для выбора наилучшего уравнения, которое бы наиболее точно отражало динамику явления или процесса, можно воспользоваться формулой стандартной ошибки:
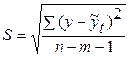 ,
,
где m – число параметров уравнения,
или применить критерий наименьшей суммы квадратов отклоненияэмпирических уровней от теоретических 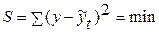 .
.
Из множества возможных уравнений тренда можно выбрать то уравнение, которому соответствует минимальное значение, т. е. критерий наименьших квадратов отклонений, либо использовать формулу средней ошибки аппроксимации:
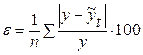 .
.
При аналитическом выравнивании может иметь место автокорреляция, под которой понимается зависимость между соседними членами динамического ряда. Автокорреляцию можно установить с помощью перемещения уровня на одну дату. Коэффициент автокорреляции вычисляется по формуле
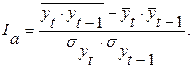
где 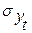 и
и 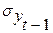 – соответственно средние квадратические отклонения по ряду
– соответственно средние квадратические отклонения по ряду 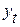 и
и 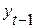 .
.
Процесс нахождения неизвестного уровня ряда, находящегося в данном динамическом ряду, называется интерполяцией.
Процесс нахождения неизвестного уровня ряда, находящегося за пределами данного ряда, называется экстраполяцией (прогноз на будущее).
Чем больше динамический ряд, тем достовернее прогноз, но, с увеличением прогнозной даты, ошибка прогноза возрастает.
Экстраполяция и интерполяция осуществляются следующими способами:
1) по среднему абсолютному приросту;
2) по среднему темпу роста;
3) по аналитическому уравнению.
Найдем прогнозное значение товарооборота на 2009 г. по данным предыдущего примера:
По среднему абсолютному приросту. Поскольку средний абсолютный прирост показывает, на сколько в среднем за год изменяется товарооборот фирмы, то для определения прогнозного значения товарооборота на 2009 г. нужно к последнему уровню ряда прибавить значение среднего абсолютного прироста:
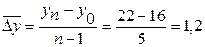 млн руб.;
млн руб.;
y2009 = 22+1,2 = 23,2 млн руб.
По среднему темпу роста. Поскольку средний темп роста показывает, во сколько раз в среднем за год увеличивается товарооборот, то для определения прогнозного значения товарооборота на 2009 г. нужно последний уровень ряда умножить на значение среднего темпа роста:
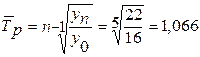 ;
;
y2009 = 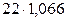 = 23,4 млн руб.
= 23,4 млн руб.
По аналитическому уравнению. В предыдущем примере (см. табл. 6.5) получили уравнение прямой линии 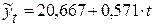 . Чтобы рассчитать прогнозное значение на 2009 г. нужно в это уравнение вместо t подставить номер 7:
. Чтобы рассчитать прогнозное значение на 2009 г. нужно в это уравнение вместо t подставить номер 7:
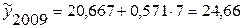 млн руб.
млн руб.
Полученные в ходе расчетов расхождения между прогнозными значениями товарооборота на 2009 г. указывают на необходимость тщательного отбора способов.
На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками.
Для определения границ интервалов используют формулу
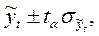
где 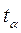 – коэффициент доверия, который определяется по таблице t –распределения Стьюдента, при уровне значимости
– коэффициент доверия, который определяется по таблице t –распределения Стьюдента, при уровне значимости 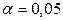 (т. е. с вероятностью P=0,95) и числе степеней свободы
(т. е. с вероятностью P=0,95) и числе степеней свободы 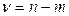 .
.
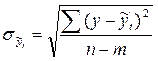 – остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (n – m),
– остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (n – m),
n – число уровней РД,
m – число параметров адекватной модели тренда (для прямой m = 2).
Определим по данным таблицы 6.5 интервальную оценку точечного прогноза на 2009 г. По таблице t –распределения Стьюдента, при уровне значимости 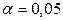 и числе степеней свободы
и числе степеней свободы 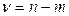 = 6 – 2 = 4, находим значение
= 6 – 2 = 4, находим значение 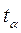 = 2,776. При
= 2,776. При 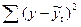 = = 32,421 (см. последнюю графу табл. 6.5) значение остаточного среднего квадратического отклонения
= = 32,421 (см. последнюю графу табл. 6.5) значение остаточного среднего квадратического отклонения 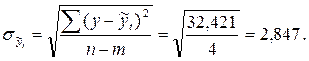
Тогда значение вероятностных границ интервала составляет 24,66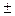 2,847×2,776. Следовательно, с вероятностью 0,95 верхняя граница прогнозного значения товарооборота фирмы на 2009 г. составит 32,64 млн руб., а нижняя граница – 16,68 млн руб.
2,847×2,776. Следовательно, с вероятностью 0,95 верхняя граница прогнозного значения товарооборота фирмы на 2009 г. составит 32,64 млн руб., а нижняя граница – 16,68 млн руб.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 567; Нарушение авторских прав?; Мы поможем в написании вашей работы!