Задачи для решения. 1. По следующим данным постройте линейное уравнение регрессии, вычислите линейный коэффициент корреляции:

1. По следующим данным постройте линейное уравнение регрессии, вычислите линейный коэффициент корреляции: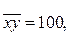

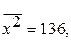
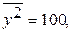
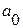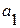2. Используя следующие данные, определите параметры линейного уравнения (и ) регрессии: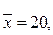

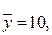
3. По следующим данным постройте линейное уравнение регрессии, вычислите линейный коэффициент корреляции: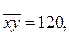

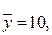
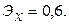
4. Имея следующие данные, постройте линейное уравнение регрессии: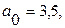

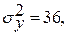
5. Имеются данные по 10 семьям об уровне доходов на 1 человека в год (х) и покупательском спросе – расходах на одежду на 1 чел. в год (у), в млн руб. Методом корреляционного анализа исследовать зависимость между этими признаками. Написать уравнение регрессии, построить эмпирические точки и линию регрессии. Найти коэффициенты корреляции и детерминации. Сформулировать выводы по результатам анализа.

х	3,4	3,1	3,0	5,0	2,8	4,1	2,5	5,3	2,9	4,0
у	0,26	0,21	0,22	0,38	0,19	0,29	0,19	0,35	0,24	0,32

6. Распределение предприятий по источникам средств на их покупку характеризуется следующими данными:

Источник средств	Зарождающийся бизнес	Зрелый бизнес	Итого
Банковский кредит Собственные средства
Итого

Вычислите коэффициенты ассоциации и контингенции. Какие выводы можно сделать на основании значений этих коэффициентов?

7. Распределение основных категорий потенциальных мигрантов по уровню образования характеризуется следующими данными:

Образование	Основные категории потенциальных мигрантов	Итого
руководители	специалисты	служащие	рабочие
Высшее Неполное высшее Среднее специальное Среднее общее Неполное среднее

Рассчитайте коэффициенты взаимной сопряженности Пирсона и Чупрова. Сформулируйте выводы, вытекающие из анализа полученных коэффициентов.

8. По данным таблицы определить зависимость между основными показателями деятельности коммерческих банков Белоруссии с помощью коэффициента конкордации.

банк	Стоимость активов, млрд нац. руб.	Кредитные вложения, млрд нац. руб.	Собственный капитал, млрд нац. руб.

9. По группе предприятий за отчетный год имеются следующие данные:

№ пред-приятия	Годовая производительность труда работника, тыс. руб.	Вооруженность труда основным капиталом, тыс. руб./чел.	Удельный вес оборудования в стоимости основного капитала	Текучесть кадров, %	Интегральный показатель использования рабочего времени
		15,2 12,8 13,8 14,0 16,3 12,6 13,2 12,9 13,1 12,5 15,7 13,5	0,39 0,29 0,34 0,36 0,47 0,28 0,32 0,29 0,33 0,28 0,40 0,34	9,1 10,1 5,0 7,0 9,0 4,0 12,0 6,5 8,0 7,0 8,5 5,0	0,96 0,80 0,84 0,86 0,98 0,83 0,87 0,84 0,81 0,85 0,97 0,83

На основании приведенных данных требуется:

1) составить уравнение множественной зависимости производительности труда, обосновав систему факторов, включенных в модель;

2) определить совокупный коэффициент корреляции и частные коэффициенты корреляции;

3) сопоставить роль различных факторов в формировании моделируемого показателя.

Тема 10

Статистические методы моделирования и прогнозирования

социально-экономических явлений и процессов

Первоначальные прогнозы, как правило, сводятся к экстраполяции тенденции. При этом могут использоваться разные методы, в зависимости от исходной информации (рис. 1).

		Методы экстраполяции тенденций
Упрощенные приемы, основанные на средних показателях динамики		Аналитические методы (кривые роста)		Адаптивные методы, учитывающие степень устаревания данных

Рис.1. Группы методов экстраполяции тенденций

Упрощенные приемы целесообразны при недостаточной информации о предыстории развития явления (нет достаточно длительного динамического ряда или информация задана только двумя точками: начало и конец периода).

Аналитические методы экстраполяции тенденций основаны на применении наименьших квадратов к динамическому ряду и представлении закономерности развития явления во времени в виде уравнения тренда, т. е. математической функции зависимости уровней динамического ряда у от фактора времени t. Используя соответствующую кривую роста, можно дать прогноз (как правило, краткосрочный).

Адаптивные методы используются в условиях сильной колеблемости уровней динамического ряда и позволяют при изучении тенденции учитывать степень влияния предыдущих уровней на последующие значения динамического ряда. К адаптивным методам относятся методы скользящих и экспоненциальных средних, метод гармонических весов, методы авторегрессионных преобразований.

Другую группу методов представляют методы статистического моделирования. Наиболее распространенные из них представлены на рис. 2

		Методы статистического моделирования
	Статические			Динамические
	Методы регрессии		Методы агрегатного моделирования динамики		Методы регрессии
единичные уравнения		система уравнений		по взаимосвязанным рядам динамики		по пространственно-временной информации

Рис. 2 Группы методов статистического моделирования

Деление методов на статические и динамические связано с характером исследуемой информации. Методы статистического моделирования могут быть использованы на основе информации в статике (по совокупности предприятий, фирм, регионов) по системе связанных рядов динамики. В первом случае они относятся к классу статических методов, а во втором – динамических.

Статические методы включают методы регрессии, с помощью которых моделируемый объект представлен в виде математической функции от ряда факторов: 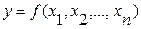. Сложные экономические процессы могут описываться системой взаимосвязанных уравнений:

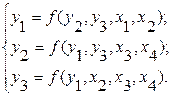
Применение этой группы методов в прогнозировании предполагает инертность процессов. Качество прогноза моделируемого объекта зависит от реальности прогноза факторов.

Динамические методы статистического моделирования основаны на подробном изучении временных рядов. В частности, уровни динамического ряда рассматриваются как функция тенденции, периодических (сезонных) и случайных колебаний. На моделировании этих компонентов разложения уровней динамического ряда основаны методы агрегатного моделирования динамики. Прогноз строится как аддитивная или мультипликативная модель этих компонентов динамики.

Регрессия по взаимосвязанным рядам динамики (особенно как система уравнений) широко применяется для прогнозирования макроэкономических показателей. При этом модель включает обычно не только набор факторов как экономических переменных, но и лаговые переменные, т. е. сдвинутые во времени на определенный интервал (например, в качестве факторов используется моделируемый показатель или собственно фактор за предыдущий год).

Своеобразие методов регрессии для прогноза имеет место при использовании пространственно-временной информации. Для каждого года динамического ряда строится регрессионная модель по совокупности предприятий. Прогноз основывается на экстраполяции параметров регрессии. Данный подход возможен в условиях достаточно стабильной экономики, когда круг охватываемых предприятий во времени мало изменчив.

Методы статистического моделирования входят в группу методов многофакторного моделирования, к которым относятся также логическое моделирование, включающее моделирование по исторической аналогии, методы сценариев и дерева целей.

Прогнозирование по исторической аналогии основано на использовании аналога объекта прогнозирования. Этот подход предполагает перенесение на новую действительность концепции развития той или иной страны, соотношение темпов роста отдельных показателей. Качество прогноза в этом случае полностью зависит от правильности выбора аналога объекта прогнозирования.

Метод сценариев, как и метод дерева целей, представляет собой метод прогнозирования сложных систем. В методе сценариев подробно описывается моделируемая ситуация и делается обзор информации, которая должна быть учтена при прогнозировании. Метод дерева целей предполагает, что для объекта прогноза существует несколько иерархических уровней, и прогноз осуществляется последовательно по отдельным стадиям, блокам – от низшего уровня к более высоким. Методы логического моделирования могут в качестве вспомогательных инструментов прогноза использовать методы экстраполяции и методы статического моделирования.

Рассмотренная классификация методов статистического прогнозирования достаточно условна, так как на практике при прогнозировании нередко методы переплетаются: методы скользящей средней дополняются уравнением тренда, авторегрессионными преобразованиями; экстраполяция тенденций дополняется авторегрессией остатков; уравнение регрессии может включать показатели тенденции развития объекта и т. п.

Элементы прогнозирования и интерполяции. Моделирование временных рядов

Выявление и характеристика основной тенденции развития при иссле­довании динамики социально-экономических явлений дают основание для прогнозирования — определения будущих размеров уровня социально-эко­номических явлений.

Применение прогнозирования предполагает, что закономерность разви­тия, действующая в прошлом (внутри ряда динамики), сохраняется в про­гнозируемом будущем, т. е. прогноз основан на экстраполяции. Экстрапо­ляция, проводимая в будущее, называется перспективой, а в прошлое — ретроспективой.

Теоретической основой распространения тенденции на будущее являет­ся свойство социально-экономических явлений, называемое инерционностью. Именно инерционность позволяет выявить сложившиеся взаимосвязи как между уровнями динамического ряда, так и между группой связанных рядов динамики. На основе рядов динамики получаются весьма надежные прогнозы, если уровни ряда динамики сопоставимы и получены на основе единой методологии.

Применение экстраполяции в прогнозировании базируется на следую­щих условиях:

• развитие исследуемого явления в целом следует описывать плавной кривой;

• общая тенденция развития явления в прошлом и настоящем не должна претерпевать серьезных изменений в будущем.

Временной горизонт экстраполяции не может быть бесконечным, потому что анализируемые временные ряды динамики нередко относительно короткие. Результат прогноза будет тем надежнее и точнее (при прочих равных условиях), чем короче срок экстраполяции (период упреждения).

Пусть имеется временной ряд {y₁, y₂, …, y_n}, взятый для простоты в равноотстоящие моменты времени. В качестве τ обозначим срок прогноза. В зависимости от принципов и исходных данных, положенных в основу прогноза, выделяют следующие элементарные методы экстраполяции: среднего абсолютного прироста, среднего темпа роста, экстраполяция на основе выравнивания рядов по какой-либо аналитической формуле.

1. С помощью среднего абсолютного прироста прогноз делается по следующей формуле:

где 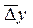– средний абсолютный прирост

2. С помощью среднего темпа роста прогноз делается по следую­щей формуле:

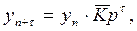
где средний коэффициент роста 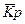наиболее хорош, когда общая тенден­ция ряда характеризуется экспоненциальной, показательной кривой.

3. Экстраполяция на основе выравнивания ряда по какой-либо кривой сводится к тому, что статистик выбирает некоторую кривую у = f(t). Дан­ная кривая определена не только для каждого имеющегося момента времени t = 1,2,..., п, но и для прогнозируемого момента времени t = п + τ.

Дата добавления: 2014-01-05