Метод изоклин

(Метод построения фазовых траекторий)

Для уравнения второго порядка применяют подстановку

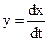(1)

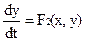
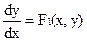(2)

Из уравнения (2) выражают некоторую N(x,y) равную

N(x,y)= 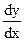(3), который будет являться значением угла фазовой траектории для определенной изоклин. Уравнение изоклин получается выраженным из уравнения (3)

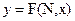(4)

Для различных значений выходного сигнала и её дифференциалов (х₁,…х_i; y₁,…y_i) определяем значения углов N₁…N_i для тех же значений х находим i уравнений (4).

Далее определяем первый изоклин. Выбираем на ней свободную точку С₀. Данному изоклин соответствует угол N₁. Наносим изоклин 2 с углом N₂ через точку С₀ проводим две линии параллельные N₁ и N₂. Точка пересечения изоклина 2 и биссектрисы угла С₀ называем точкой С₁. Также определяем последующие точки N. Точки С₀,…,С_i образуют фазовую траекторию.

Пример:

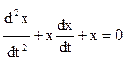
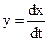
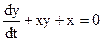
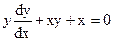
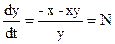
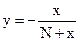
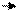
N_i N₁

N₂

x

Дата добавления: 2014-01-05