Принципы управления СЭУ

1) Управление по возмущению

Рассмотрим семейство экстремальных характеристик:

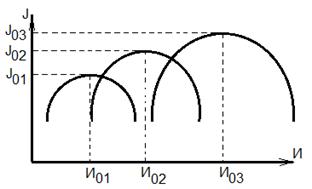
В случаях, когда возмущающее воздействие f можно измерить, допустимо использование некоторых компенсационных характеристик

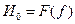
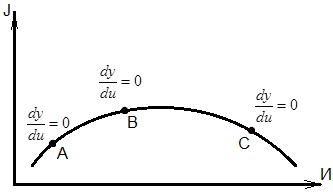
2) Принцип управления по отклонению

Для того, чтобы организовать управление, необходимо вычислить частную производную и организовать воздействие на ОУ таким образом, чтобы рассматриваемая производная стремилась к нулю или находилась в окрестностях точки экстремума системы.

Таким образом, синтез системы преследует цели о нахождении такой структуры системы адаптивного управления, при ктр выполняется условие (1)

Таким образом, получим:

;

;

Существуют многомерные экстремальные ОУ в которых имеется много входов и выходов.

I

В случае многомерных объектов для движения к экстремуму необходимо знать градиент. Векторы проекции градиента на оси буду равны ; ; …;

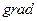
МЕТОДЫ ДВИЖЕНИЯ ЭКСТРЕМУМА

1. Метод градиентного спуска (в каждом цикле движения точки выбирается направление наибольшего подъема I)

2. Метод наискорейшего спуска

Цель управления – найти U_опт1 и U_опт2

Так как функция качества неизвестна, организовывается градиентный поиск.

В точке А выбирается направление движения, которое продолжается до тех пор, пока не прекратится рост критерия качества, то есть пока градиент не станет равным нулю по данному направлению. Шаг заканчивается в точке А₂. В ней вычисляется новый градиент и движение будет идти пока увеличивается критерий качества до точки А₃ и так далее.

Отличие данного метода в том, что новый градиент вычисляется после изменения знака критерия качества.

3. Метод Гаусса-Зейделя

Движение осуществляется только по одной координате, вторая координата постоянна до нахождения экстремума по данной координате

4. Метод случайного поиска

В точке А производится пробное движение по четырем основным направлениям. В каждой точке поиска осуществляется пробное движение в 3-х направлениях. Направление с наибольшей разностью критерия качества является конечным. Метод является самым несовершенным с точки зрения времени поиска, но показывает наилучшие результаты при наличии нескольких или локальных экстремумов.

МЕТОДЫ ОПРЕДЕЛЕНИЯ ГРАДИЕНТОВ

В системах экстремального управления (СЭУ) определение градиента является ключевым моментом. Управляющее воздействие напрямую зависит от знака и значения градиента. Рассмотрим несколько методов:

Метод синхронного детектирования

С целью описания градиента dJ/du, на выход ОУ подается гармоническое колебание небольшой амплитуды

(1)

Из курсов высшей математики известно, что при гладких статических характеристиках объекта, выходной сигнал может быть разложен в степенной ряд Тейлора.

(2)

Ограничимся двумя составляющими выражения

(3)

Выражение (3) запишем с учетом выражения (1)

(4)

Выражение (4) умножим на выражение (1) и получим:

(5)

Если пропустить сигнал, описывающийся выражением (5) через фильтр, то можно получить некоторые усредненные значения составляющих выражения

1)

2)

С учетом вышесказанных допущений, можно записать следующую зависимость:

Таким образом получим сигнал Z, пропорциональный градиенту С с помощью дополнительного гармонического сигнала.

Для технической реализации данной процедуры, необходимо выходной сигнал OУ умножить на гармонический сигнал

Данная процедура называется синхронным детектированием и схематично синхронный детектор можно изобразить так:

Схема оптимального управления будет иметь вид:

Далее, данная схема будет нуждаться в дополнительных настройках К – коэффициента передачи регулятора, А – амплитуды гармонического сигнала и - частоты гармонического сигнала.

Данный метод используется при управлении многомерными объектами, тогда оптимизация будет являться многомерной.

Достоинства:

Простота технической реализации, высокая устойчивость к помехам, большое быстродействие при управлении многомерными объектами.

Недостатки:

1) Трудности управления инерционными объектами.

2) Трудности предварительной настройки коэффициентов передачи регулятора и параметров гармонических сигналов при многомерном управлении.

МЕТОД ПРОИЗВОДНОЙ ПО ВРЕМЕНИ

Градиент (grad) для экстремального объекта можно получить в результате отношения производной по времени выходного сигнала на производную по времени входного сигнала

Достоинства:

Простота реализации.

Недостатки:

1) Возникают случаи, когда производные входного сигнала 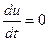, данного положения можно избежать введением в цепь

2) 2) Изменение производной выходного сигнала может быть вызвано так же возмущающим воздействием f, что увеличит время поиска.

3) Трудно реализовать дифференцирующее устройство в природе. Решением этого является дифференциальное звено с фильтрованием:

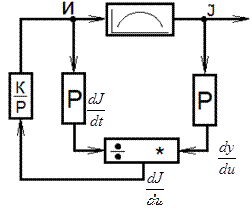
СИСТЕМА ЭКСТРЕМАЛЬНОГО УПРАВЛЕНИЯ (СЭУ) С ПРОИЗВОДНОЙ ПО ВРЕМЕНИ И С ПОМОЩЬЮ РЕЛЕ С ГИСТЕРЕЗИСОМ

Рассмотрим статическую характеристику объекта управления. В точке А получаем , соответственно выход гистерезиса буде положительным. Через интегрирующий регулятор, сигнал подается в объект управления, входной сигнал передвигает рабочую точку из точки А, в направлении экстремума (в точку В). Из-за наличия зоны нечувствительности, рабочая точка переходит экстремум, и достигает точки С.

При этом скорость становится < 0 и принимает отрицательный знак. Реле выдает сигнал , в результате чего, рабочая точка из точки С, начинает движение к экстремуму обратно. Таким образом, рабочая точка ОУ, находится в окрестностях экстремума. При малом параметре петли гистерезиса, можно достичь соответствующую точность.

Дата добавления: 2014-01-05