Цепи Маркова

Марковский процесс - протекающий в системе случайный процесс, который обладает свойством: для каждого момента времени t₀ вероятность любого состояния системы в будущем (при t>t₀) зависит только от ее состояния в настоящем (при t= t₀) и не зависит от того, когда и каким образом система пришла в это состояние (т.е. как развивался процесс в прошлом).

На практике часто встречаются случайные процессы, которые с той или иной степенью приближения можно считать Марковскими.

Любой марковский процесс описывают с помощью вероятностей состояний и переходных вероятностей.

Вероятности состояний P_k(t) марковского процесса – это вероятности того, что случайный процесс (система) в момент времени t находится в состоянии S_k:

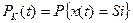
Переходные вероятности марковского процесса – это вероятности перехода процесса (системы) из одного состояния в другое:

Марковский процесс называется однородным, если вероятности перехода за единицу времени не зависят от того, где на оси времени происходит переход.

Наиболее простым процессом является цепь Маркова – марковский случайный процесс с дискретным временем и дискретным конечным множеством состояний.

При анализе цепи Маркова составляют граф состояний, на котором отмечают все состояния цепи (системы) и ненулевые вероятности за один шаг.

Марковскую цепь можно представить себе так, как будто точка, изображающая систему, случайным образом перемещается по графу состояний, перетаскивая за один шаг из состояния в состояние или задерживаясь на несколько шагов в одном и том же состоянии.

Переходные вероятности цепи Маркова за один шаг записывают в виде матрицы P=||P_ij||, которую называют матрицей вероятностей перехода или просто переходной матрицей.

Пример: множество состояний студентов специальности следующие:

S₁ – первокурсник;

S₂ – второкурсник …;

S₅ – студент 5 курса;

S₆ –специалист, окончивший вуз;

S₇ – человек, обучавшийся в вузе, но не окончивший его.

Из состояния S₁ за год возможны переходы в состояние S₂ с вероятностью r₁; S₁ с вероятностью q₁ и S₇ с вероятностью p₁, причем:

r₁+q₁+p₁=1.

Построим граф состояний данной цепи Маркова и разметим его переходными вероятностями (отличными от нуля).

Составим матрицу вероятностей переходов:

Переходные матрицы обладают свойством:

- все их элементы неотрицательны;

- их суммы по строкам равны единице.

Матрицы с таким свойством называют стохастическими.

Матрицы переходов позволяют вычислить вероятность любой траектории цепи Маркова с помощью теоремы умножения вероятностей.

Для однородных цепей Маркова матрицы переходов не зависят от времени.

При изучении цепей Маркова наибольший интерес представляют:

- вероятности перехода за m шагов;

- распределение по состояниям на шаге m→∞;

- среднее время пребывания в определенном состоянии;

- среднее время возвращения в это состояние.

Рассмотрим однородную цепь Маркова с n состояниями. Для получения вероятности перехода из состояния S_i в состояние S_j за m шагов в соответствии с формулой полной вероятности следует просуммировать произведения вероятности перехода из состояния Siв промежуточное состояние Sk за l шагов на вероятность перехода из Sk в Sj за оставшиеся m-l шагов, т.е.

Это соотношение для всех i=1, …, n; j=1, …,n можно представить как произведение матриц:

P(m)=P(l)*P(m-l).

Таким образом, имеем:

P(2)=P(1)*P(1)=P²

P(3)=P(2)*P(1)=P(1)*P(2)=P³ и т.д.

P(m)=P(m-1)*P(1)=P(1)*P(M-1)=P^m,

что дает возможность найти вероятности перехода между состояниями за любое число шагов, зная матрицу переходов за один шаг, а именно P_ij(m) – элемент матрицы P(m) есть вероятность перейти из состояния S_i в состояние S_j за m шагов.

Пример: Погода в некотором регионе через длительные периоды времени становится то дождливой, то сухой. Если идет дождь, то с вероятностью 0,7 он будет идти на следующий день; если в какой-то день сухая погода, то с вероятностью 0,6 она сохраниться и на следующий день. Известно, что в среду погода была дождливая. Какова вероятность того, что она будет дождливой в ближайшую пятницу?

Запишем все состояния цепи Маркова в данной задаче: Д – дождливая погода, С – сухая погода.

Построим граф состояний:

Составим матрицу вероятностей перехода:

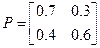
Ответ: р₁₁=р(Д_пят|Д_ср) =0,61.

Пределы вероятностей р₁(m), р₂(m),…, р_n(m) при m→∞, если они существуют, называются предельными вероятностями состояний.

Можно доказать следующую теорему: если в цепи Маркова из +каждого состояния можно перейти (за то или иное число шагов) в каждое другое, то предельные вероятности состояний существуют и не зависят от начального состояния системы.

Таким образом, при m→∞ в системе устанавливается некоторый предельный стационарный режим, при котором каждое из состояний осуществляется с некоторой постоянной вероятностью.

Вектор р, составленный из предельных вероятностей, должен удовлетворять соотношению: р=p*P.

Среднее время пребывания в состоянии S_i за время T равно p_i*T, где p_i - предельная вероятность состояния S_i. Среднее время возвращения в состояние S_i равно .

Пример.

Для многих экономических задач необходимо знать чередование годов с определенными значениями годовых стоков рек. Конечно, это чередование не может быть определено абсолютно точно. Для определения вероятностей чередования (перехода) разделим стоки, введя четыре градации (состояния системы): первую (самый низкий сток), вторую, третью, четвертую (самый высокий сток). Будем для определенности считать, что за первой градацией никогда не следует четвертая, а за четвертой – первая из-за накопления влаги (в земле, водохранилище и т.д.). Наблюдения показали, что в некоторой области остальные переходы возможны, и:

а) из первой градации можно переходить в каждую из средних вдвое чаще, чем опять в первую, т.е.

p₁₁=0,2; p₁₂=0,4; p₁₃=0,4; p₁₄=0;

б) из четвертой градации переходы во вторую и третью градации бывают в четыре и пять раз чаще, чем возвращениеекак д во вторую, т.е.

твертую, т.е.

в четвертую, т.е.

p₄₁=0; p₄₂=0,4; p₄₃=0,5; p₄₄=0,1;

в) из второй в другие градации могут быть только реже: в первую - в два раза, в третью на 25%, в четвертую - в четыре раза реже, чем переход во вторую, т.е.

p₂₁=0,2;p₂₂ =0,4; p₂₃=0,3; p₂₄=0,1;

г) из третьей градации переход во вторую градацию столь же вероятен, как возвращение в третью градацию, а переходы в первую и четвертую градации бывают в четыре раза реже, т.е.

p₃₁=0,1; p₃₂=0,4; p₃₃=0,4; p₃₄=0,1;

Построим граф:

Составим матрицу вероятностей перехода:

P=

Найдем среднее время между засухами и полноводными годами. Для этого нужно найти предельное распределение. Оно существует, т.к. условие теоремы выполняется (матрица Р² не содержит нулевых элементов, т.е. за два шага можно перейти из любого состояния системы в любое другое).

Используем соотношение: p=p*P.

Запишем его в виде системы:

= *

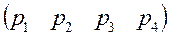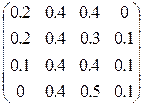
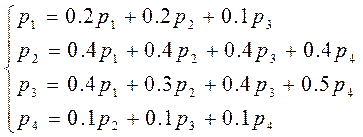
или

Это однородная система линейных алгебраических уравнений. Ее можно решить, например, методом Гаусса. Для этого необходимо привести матрицу системы к треугольному виду:

вычтем из 3 вторую сложим вторую с

первой *2 сложим 2 и 3 и эту сумму прибавим к 4

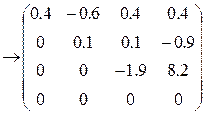
вычтем из 3-ей вторую, умноженную на 9

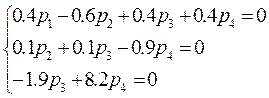
Система приведена к треугольному виду. Но мы имеем 3 уравнения и 4 неизвестных. Добавим условие p₁+p₂+p₃+p₄=1, т.к. система обязательно находится в одном из своих состояний.

Получим:

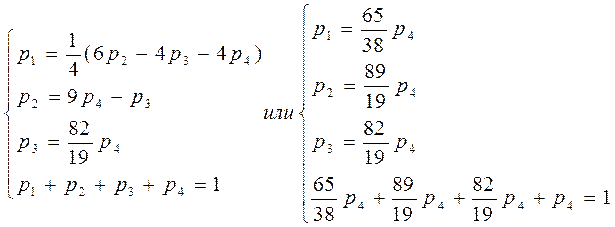П

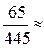Откуда p₄ =0.08; p₃=; p₂=; p₁=0.15

Периодичность возвращения в состояние S_i равна .

Следовательно, периодичность засушливых лет в среднем равна 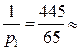6.85, т.е. 6-7 лет, а дождливых 12 лет.

Дата добавления: 2014-01-05