Границы зерен, выросших из разных центров при кристаллизации и фазовых превращениях в твердом состоянии, чаще всего бывают высокоугловыми

ВЫСОКОУГЛОВЫЕ ГРАНИЦЫ

Высокоугловые границы — это «старейший» вид дефектов кристаллического строения металлов, обнаруженный в самых ранних металлографических работах при изучении под микро­скопом протравленной поверхности шлифов.

Хотя описанию границ зерен, обсуждению их строения и по­ведения посвящена обширная литература, до сих пор строгая общая теория высокоугловых границ не создана. Из-за отсутствия прямых структурных методов длительное время модели атомного строения границ проверялись, по тому, насколько хорошо они согласовывались с известными свойствами и поведением границ. В последнее время достигнут значительный прогресс благодаря прямому исследованию атомного строения границ зерен с помощью ионного проектора с разрешающей способностью до , примене­нию дифракционной электронной микроскопии тонких фольг, со­держащих высокоугловую границу, а также благодаря появлению новых идей относительно моделей атомного строения высоко­угловых границ.

В начале столетия была предложена модель аморфной прослойки по границам зерен, аморфного «цемента», обеспечивающего сцеп­ление соседних кристаллов. Взаимное смещение зерен как еди­ного целого во время высокотемпературной деформации объяс­няли тем, что с повышением температуры аморфные прослойки* размягчаются быстрее, чем кристаллические зерна.

Модель аморфной прослойки оказалась противоречащей мно­гим позднее экспериментально установленным фактам. Во-первых, свойства аморфной границы не должны зависеть от разницы в кристаллографической ориентации зерен по обе стороны от границы. В действительности же энергия границ зерен, скорость диффузии по границам, скорости миграции границ и зернограничного скольжения, а также другие характеристики границ зависят от угла разориентировки зерен. Следовательно, границы не аморфны, не бесструктурны, а должны иметь определенное строе­ние, зависящее от кристаллографической разориентировки зерен. Во-вторых, аморфная прослойка должна иметь достаточно боль­шую ширину (например, порядка ста атомных диаметров), чтобы по ней могли взаимно скользить зерна неправильной формы. В то же время на основании косвенных, а затем и прямых экспе­риментальных данных, полученных с помощью ионного проектора, был сделан вывод, что ширина границы составляет всего 1—2 атомных диаметра.

В 1929 г. Харгривс и Хилл предложили модель переходной решетки. Согласно этой модели граница является слоем толщиной 1—2 атомных диаметра, в котором атомы занимают такие поло­жения, компромиссные между положениями узлов решеток со­седних зерен, чтобы потенциальная энергия атомов в этом слое была минимальной. Естественно, что строение границы — пере­ходной зоны зависит от разориентировки решеток соседних зерен, чем и обусловлено влияние этой разориентировки на свой­ства и поведение границ. Из гипотезы переходной решетки по существу исходят все современные модели строения высокоугло­вых границ.

Следующим важным шагом в изучении границ зерен была островковая модель Мотта (1948 г.), согласно которой граница представлялась в виде островков «хорошего» сопряжения решеток двух зерен, окруженных областями «плохого» сопряжения. Число островков хорошего сопряжения тем меньше, чем больше угол разориентировки соседних зерен. Хотя эту модель в ее первона­чальном виде уже не используют, но общую идею о чередовании в структуре границы областей хорошего и плохого сопряжения широко применяют в большинстве современных моделей высоко­угловых границ. Простейшая дислокационная модель малоугло­вой границы (см. рис. 104, б) также включает представление о чередовании этих областей — ядер дислокаций (плохое сопря­жение) и участков хорошего упругого сопряжения решеток между дислокациями. Основной вопрос, который обсуждается в настоящее время, — каковы особенности расположения атомов в участках плохого и хорошего сопряжения на высокоугловых границах.

В развитии представлений о строении высокоугловых границ большую роль играют так называемые особые (специальные) гра­ницы, отличающиеся пониженной энергией и отвечающие особым кристаллографическим разориентировкам соседних зерен. Как показали Кронберг и Вильсон, при развороте двух одинаковых решеток вокруг общей кристаллографической оси на определенный угол, часть узлов одной решетки совпадает с узлами другой решетки. Такие узлы совпадения (рис. 117) образуют свою трехмерную «сверхрешетку» — решетку уз­лов совпадения (коротко — решетку совпадения), общую для обоих зерен. Характерным дискретным углам по­ворота (соотношениям Кронберга — Вильсона) соответствует определен­ная плотность узлов совпадения, т. е. их доля по отношению ко всем узлам решетки металла. Например, на рис. 117 при угле разворота 36,9° вокруг оси (001) решетка совпаде­ния образована каждым пятым ато­мом соседних зерен, т. е. плотность узлов совпадения равна 1/5.

Для характеристики решетки сов­падения чаще используют не плот­ность узлов совпадения, а обратную ей величину, обозначаемую Σ — чи­сло узлов решетки металла, прихо­дящихся на один узел совпадения в общей сверхрешетке. Например, в случае, изображенном на рис. 117, Σ=5.

При любой разориентировке решеток соседних зерен можно найти некоторое число узлов совпадения. Но при низкой их плотности понятие об общей сверхрешетке практически, теряет смысл для анализа строения границ зерен. Обычно рассматривают решетки совпадения при значениях Σ находящихся в интервале от 3 до 19 (при Σ = 1 угол разориентировки равен нулю). В табл. 5 в качестве примера приведены значения Σ для разных условий совпадения. Здесь же указаны плоскости с наибольшей плотностью узлов совпадения.

Если граница зерен проходит вдоль плоскости с максимальной плотностью узлов совпадения (см. рис. 117), то из-за большого числа атомов, принадлежащих одновременно решеткам соседних зерен, структура границы совпадения весьма совершенна и соот­ветственно ее энергия минимальна. Такая граница, называемая также границей Кронберга — Вильсона, является особой (специальной), отличающейся по своему поведению от произвольных границ.

Если граница зерен находится под небольшим углом к плотно-упакованной плоскости в решетке совпадения, то она может иметь ступенчатое строение (рис. 118), что обеспечивает минимум энер­гии. При этом граница стремится расположиться большей частью своей поверхности в плоскостях с максимальной плотностью узлов совпадения, где наиболее совершенно сопряжение решеток двух зерен, минимальны энергия и ширина границы (см. участки АВ и CD на рис. 118). Эти участки границы соединены ступенькой (ВС), высота которой определяется расстоянием между плоско­стями с максимальной плотностью узлов совпадения. Число ступенек на единице длины границы зерен тем больше, чем силь­нее ее макроскопическая ориентация отклоняется от плоскости с наибольшей плотностью узлов совпадения.

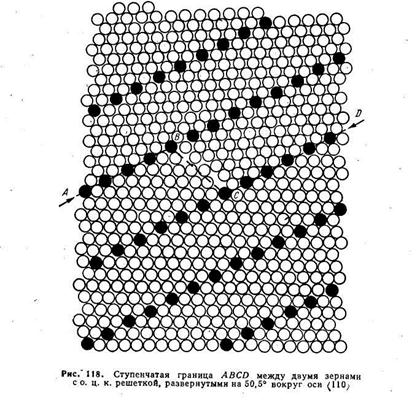На рис. 118 видно, что вдоль ступеньки ВС решетки соседних зерен плохо сопряжены и граница здесь шире. Таким образом, рассматриваемая ступенчатая граница представляет собой чередование областей хорошего и плохого сопряжения решеток соседних зерен, причем плохое сопряжение сосредоточено на небольших участках (ступеньках). Подобные ступенчатые границы неоднократно наблюдали при исследовании тугоплавких металлов с помощью ионного проектора.

Решетки совпадения с Σ = 3, 5, 7 и т. д. существуют при строго определенных ориентационных соотношениях решеток двух зерен (см. табл. 5). Любое небольшое отклонение от идеального ориентационного соотношения приводит к исчезновению общей сверхрешетки с высокой плотностью узлов совпадения на границе зерен.

Однако эксперименты показывают, что свойства и поведение особых границ при этом скачком не меняются. Следо­вательно, при отклонениях разориентировки зерен от идеального соотношения Кронберга—Вильсона строение границы изменяется плавно, а не скачкообразно. В модели строения межзеренной границы это должно быть учтено. Кроме того, в модели жестких сфер нерелаксированная идеальная граница совпадения не соот­ветствует минимуму энергии. На рис. 119 показаны физически невозможные перекрытия жестких сфер (атомов) двух зерен справа от узлов совпадения А и В и участки отсутствия контакта зерен между этими узлами (большой избыточный объем на гра­нице по сравнению с совершенной решеткой внутри зерен).

Глейтер и Чалмерс в 1971 г. предложили модель строения границы, лишенную недостатков модели узлов совпадения. Если два кристалла взаимно ориентированы так, что существует решетка совпадения, то граница совпадения имеет периодическое строение. Ее можно рассматривать как состоящую из одинаковых сегментов (АВ на рис. 119 или Р на рис. 120, а), являющихся «единицей повторяемости» двумерной периодической структуры.

Чтобы в пределах сегмента Р (рис. 120, а) уменьшить сумму энергий парных взаимодействий атомов соседних кристаллов, необходимо, как показывают расчеты, сместить кристаллы один относительно другого (без вращения), выведя границу из поло­жения узлов совпадения (рис. 120, б). При такой «жесткой ре­лаксации» каждый атом остается в узле решетки своего кристалла. Важно подчеркнуть, что хотя границы узлов совпадения после такого смещения зерен уже не существует, периодичность строе­ния границы сохраняется и сохраняется сегмент повторяемости Р (рис. 120, б), равный соответствующему сегменту в идеальной границе совпадения (рис. 120, а).

В дальнейшем сумма энергии парных взаимодействий в пре­делах сегмента Р может уменьшиться вследствие индивидуальных смещений атомов из их исходных узлов. Большинство атомов должно релаксировать так, чтобы улучшился контакт соседних зерен вдоль сегмента повторяемости. При этом по обе стороны от границы решетка должна деформироваться на расстояние, соизмеримое с длиной сегмента Р. Избыточная энергия (в рас­чете на единицу площади границы) тем меньше, чем меньше сегмент повторяемости.

Предполагается, что особыми (специальными) границами, отличающимися пониженной энергией и повышенной подвиж­ностью, являются границы с малым сегментом повторяемости (6 атомов и менее на длине сегмента вдоль границы). Малый размер сегмента в структуре релаксированной границы Глейтера - Чалмерса (рис. 120,6) соответствует малому разме­ру элементарной ячейки сверхрешетки, т. е. высокой плотности узлов совпадения, которая в модели Кронберга—Вильсона характеризует строение особых границ.

Таким образом, хотя ре­альная структура границ и не описывается моделью уз­лов совпадения, особые ориентационные соотношения решеток соседних зерен оп­ределяют малую величину сегмента повторяемости в периодической структуре гра­ниц и обусловливают тем самым их особые свойства.

При небольших отклоне­ниях взаимной ориентации решеток соседних зерен от особой периодичность строе­ния границы, состоящей из небольших сегментов, не исчезает скачком, а посте­пенно изменяется, обуслов­ливая плавное изменение энергии, подвижности и дру­гих свойств.

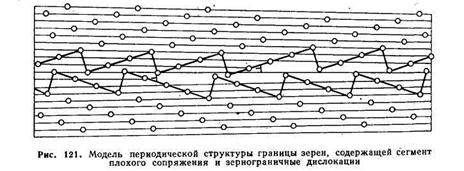
Значительные отклонения от особых ориентации можно полу­чить, если представить границу состоящей из сегментов разного размера, например длиной не только 4, но и 5 атомных диаметров (рис. 121). Чтобы при этом сохранялась хорошая сопряженность зерен, их решетки должны претерпеть определенную упругую деформацию. С увеличением отклонения от идеальной ориентации зерен поле деформации должно быть больше и соответственно энергия, связанная с такой границей, также будет больше. «Сме­шивая» сегменты разной длины в разной пропорции, можно по­лучить модели строения границ с произвольной ориентацией.

В последние годы все большее развитие получает описание Структуры высокоугловых границ на базе представлений о зернограншных дислокациях (ЗГД). Эти дефекты структуры границ зерен выявляются в виде тонких линий методом дифракционной электронной микроскопии тонких фолы, содержащих высоко­угловую границу.

Первоначально представления о ЗГД были введены для того, чтобы описать атомный механизм зернограничного скольжения — смешение одного зерна относительно другого под действием приложенных напряжений. Гра­ница зерна имеет, как отме­чалось, периодическое строе­ние. ЗГД отделяет ту часть межзеренной границы, где сдвиг уже прошел и восста­новилось исходное периоди­ческое строение границы, от той части, где он еще не на­чинался. На рис. 122 пока­зана краевая ЗГД, являю­щаяся областью несовершен­ства на границе зерен вокруг края двух «лишних» плоско­стей в верхнем зерне. Век­тор Бюргерса такой ЗГД лежит в плоскости границы, и ЗГД может скользить в этой плоскости. При сколь­жении ЗГД в каждый момент в сдвиге участвуют только те атомы, которые находят­ся в области ядра дислокации. Продвижение одной дислокации по поверхности раздела соседних зерен вызывает их взаимное смещение на величину вектора Бюргерса ЗГД. Здесь полная аналогия со скольжением решеточных дислокаций, т. е. дислока­ций внутри зерен (см. § 10).

Если учесть, что после прохождения ЗГД периодическая структура границ восстанавливается, то вектор Бюргерса ЗГД является наименьшим возможным вектором периодической струк­туры границы. Так как периодическая структура границы зависит от взаимной кристаллографической ориентировки зерен и ориен­тации самой границы, то ЗГД могут иметь разнообразные векторы Бюргерса, в общем случае отличающиеся от вектора Бюргерса решеточных дислокаций.

Консервативное движение (скольжение) ЗГД, не связанное с переносом массы, возможно только на плоских участках гра­ницы зерен. Плоские участки, часто очень короткие, наблюдают под микроскопом. Так как вся граница зерен не идеально пло­ская, то ЗГД могут перемещаться на значительные расстояния вдоль границы только при сочетании скольжения и переползания. ЗГД образуют нагромождения у препятствий. Противополе от скопления зернограничных дислокаций приводит к затуханию их источника (например, типа Франка—Рида) и при постоянном приложенном напряжении зернограничное скольжение затухает. При повышенных температурах нагромождения ЗГД у препят­ствий рассасываются переползанием, и тогда зернограничное скольжение может продолжаться.

Выше рассматривались образовавшиеся при пластической деформации зернограничные дислокации, которые всегда являются неравновесными дефектами структуры границы.

Существуют внутренние ЗГД, присущие данной границе, являющиеся неотъемлемым элементом ее структуры, не связанным с пластической деформацией под действием приложенных напря­жений. Например, при отклонении ориентации решеток зерен от особого ориентационного соотношения наличие сегментов повторяемости разной длины равносильно существованию дисло­каций в структуре границы (см. рис. 121).

Сетка внутренних ЗГД обеспечивает минимум энергии высокоугловой границы при отклонении ориентации решеток соседних зерен от особой.

Вектор Бюргерса внутренних ЗГД зависит от структуры границы. Например, в случае кристаллов золота внутренние ЗГД при отклонении от особых ориентации границы кручения вокруг направления (100) имеют тем меньший вектор Бюргерса, чем
больше Σ:

Расстояние между внутренними ЗГД в их равновесной сетке обратно пропорционально углу отклонения от особой ориентации. Здесь полная аналогия с влиянием разориентировки на расстоя­ние между дислокациями в малоугловой границе [см. рис. 104, б и формулу (65)], в которой дислокации, обеспечивающие минимум энергии сопряжения слегка разориентированных решеток, яв­ляются не специфическими зернограничными, а обычными ре­шеточными (для малоугловой границы Σ = 1).

Модель сетки внутренних ЗГД, встроенной в особую границу для обеспечения минимума энергии при отклонениях разориен­тировки зерен от особой, может описать строение широкого набора произвольных высокоугловых границ. Эта модель в прин­ципе может быть использована в случаях разнообразных значений Σ и отклонений от осо­бых ориентационных соотношений. Экспериментально же сетку внут­ренних ЗГД пока наблюдали толь­ко при сравнительно небольших значениях Σ и малых отклоне­ниях от особых разориентировок, так как уменьшение вектора Бюргерса с увеличением Σ и уменьшение расстояния между зернограничными дислокациями с увеличением угловых отклонений от особых разориентировок за­трудняют или делают совсем не­возможным наблюдение внутрен­них ЗГД.

К линейным дефектам струк­туры границ зерен, кроме зернограничных дислокаций, относятся также ступеньки, которые прямо выявляются при изучении атом­ного строения высокоугловых гра­ниц с помощью ионного проектора. По своим свойствам и поведению зернограничные ступеньки могут существенно отличаться от ЗГД и могут быть органически связаны с зернограничными дислокациями.

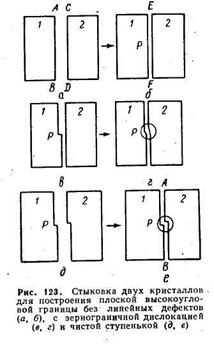
С помощью рис. 123 можно сопоставить ЗГД и зернограничные ступеньки. Если два исходных кристалла 1 и 2 с разной простран­ственной кристаллографической ориентировкой, имеющих плоские грани АВ и CD (рис. 123, а), плотно соединить, то образуется бикристалл с плоской высокоугловой границей EF (рис. 123,6). На такой границе нет ни ЗГД, ни ступенек. Сделаем сверху вниз вырез по плоскости EF до некоторой точки Р, удалив часть кри­сталла 1 (рис. 123, в). Если теперь плотно соединить оба кри­сталла вдоль всей их поверхности раздела, то на восстанов­ленной высокоугловой границе у точки Р появится дислокация (рис. 123, г).

Вдоль линии, ограничивающей зону сдвига (на рис. 123, г эта линия выходит на плоскость чертежа в точке Р), в области ядра дислокации (внутри круга) атомы сильно смещены от своих нормальных положений на границе и точное их размещение не­известно. Вокруг ЗГД на рис. 123, г решетка кристаллов упруго искажена, существует дальнодействующее поле напряжений. Если в бикристалле с ЗГД на рис. 123, г провести замкнутый контур вокруг точки Р, то соответствующий контур в исходном бикристалле, не содержащем ЗГД, будет не замкнут на величину вектора Бюргёрса. Здесь полная аналогия с описанием решеточ­ных дислокаций в § 9 и 15. В случае рис. 123, г вектор Бюргёрса перпендикулярен плоскости высокоугловой границы. В других случаях он может находиться в плоскости границы или распо­лагаться под любым углом к ней.

Теперь допустим, что на соседних гранях исходных кристал­лов / и 2 с разной кристаллографической ориентировкой имеются ступеньки одинаковой высоты (рис. 123, д). После плотной сты­ковки этих кристаллов на высокоугловой границе А В появляется линейный дефект недислокационного характера (рис. 123, е). Этот дефект у точки Р является совершенной или чистой ступень­кой. В отличие от ЗГД вокруг чистой ступеньки нет дальнодействующего поля упругих напряжений, а вектор. Бюргёрса сту­пеньки равен нулю.

Чистая ступенька и дислокация могут мигрировать вдоль границы, но механизм и результаты этой миграции существенно различаются.

Ступенька мигрирует путем перехода атомов от одного кри­сталла к другому на короткие расстояния в пределах самой сту­пеньки (внутри круга на рис. 123, е). Например, при переходе атомов в области ступеньки от кристалла 2 к кристаллу 1 сту­пенька продвигается вверх вдоль высокоугловой границы, а сама граница таким способом смещается в направлении, перпендику­лярном своей плоскости, в стороны «поедаемого» кристалла 2. Следовательно, в результате миграции ступеньки вдоль высоко­угловой границы перемещается сама граница.

Миграция чистой ступеньки вдоль границы не приводит к взаимному смещению кристаллов по их поверхности раздела, в то время как движение ЗГД вдоль границы (переползанием или скольже­нием) вызывает взаимное смещение соседних зерен-.

Переползание вдоль границы зернограничной дислокации, у которой составляющая вектора Бюргерса перпендикулярна плоскости границы (рис. 123, г), связано с испусканием или абсорбцией точечных дефектов, например вакансий. Соответ­ственно высокоугловая граница, содержащая такие ЗГД, служит эффективным источником или стоком точечных дефектов.

Переползание ЗГД вдоль границы на рис. 123, г приводит к миграции границы в направлении, перпендикулярном ее пло­скости. Например, присоединение вакансий к выступу кристалла / на рис. 123, г приводит к смещению границы в сторону этого кристалла.

Следовательно, миграция высокоугловой границы может про­исходить в результате движения и ступенек и ЗГД в плоскости границы, а взаимное смещение зерен — только при движении ЗГД.

Скорость миграции границы зависит от температуры, содер­жания примесей, угловой разориентировки зерен и других фак­торов. Процесс миграции границ в общем сводится к самодиф­фузии — переносу атомов от одного зерна к другому в направле­нии, обратном направлению движения границы. Поэтому скорость миграции растет с повышением температуры. Примеси, притяги­ваясь к границе, тормозят ее миграцию, так как мигрирующая граница должна тащить за собой примесную атмосферу. Особые границы (см. рис. 117), имея более совершенное.строение, чем произвольные, слабее притягивают к себе примесные атомы и поэтому быстрее мигрируют. Скорость миграции особых границ может быть на два порядка больше, чем у произвольных., Эксперименты показывают, что высокой подвижностью обла­дают границы при разориентировке соседних зерен, несколько отклоняющейся от идеального соотношения Кронберга—Виль­сона, которое обеспечивает большую плотность узлов совпадения. Это предположительно объясняют тем, что небольшие отклонения от структуры идеального совпадения узлов еще не вызывают силь­ного притяжения примесных атомов к границе, но делают границу несколько «рыхлой», чем обеспечивается переход атомов от зерна к зерну.

Миграция высокоугловых границ — это один из важнейших процессов, обеспечивающих развитие рекристаллизации и раз­нообразных фазовых превращений в твердом состоянии.

Дата добавления: 2014-01-05