Сила Пайерлса

ТОРМОЖЕНИЕ ДИСЛОКАЦИЙ

Скользящие дислокации всегда тормозятся, часто вплоть до полной остановки, под действием разнообразных факторов. Изу­чение этих факторов представляет исключительно большой инте­рес, так как с торможением дислокаций прямо связаны важней­шие механические свойства и прежде всего прочность металлов. Даже в кристалле, свободном от других дефектов, скольжению дислокации препятствуют силы «трения», обусловленные перио­дическим полем решетки. Основное тормозящее действие на скользящую дислокацию оказывают другие дислокации, точеч­ные и поверхностные дефекты, в громадном числе находящиеся в реальных металлических кристаллах.

Рассмотрим, какое минимальное (критическое) касательное напряжение требуется для движения краевой дислокации в кри­сталле, свободном от других дефектов.

В исходном состоянии в результата симметрии горизонтальные составляющие сил, действующих на атом 1 со стороны соседей слева и справа от него, взаимно уравновешиваются (см. рис. 25). То же самое справедливо по отношению к атому 14, соответствую­щему новому (соседнему) положению дислокации. Казалось бы, что сила, необходимая для перемещения дислокации на одно межатомное расстояние, бесконечно мала. Однако в период пере­мещения дислокации в соседнее положение из-за смещений ато­мов симметрия межатомных сил нарушается. Чтобы дислокация преодолела потенциальный барьер, разделяющий два соседних ее положения в энергетических ямах (точки 1 и 14 на рис. 25), необходима сила. Она называется силой Пайерлса (или силой Пайерлса — Набарро). Поскольку эта сила определяется свой­ствами решетки, то говорят о силах «трения» в решетках. Учи­тывая, что сила, действующая на единицу длины дислокации f=bτ, можно для силы Пайерлса записать: f_п=bτ_п, где b — вектор Бюргерса, а τ_п — минимальное касательное напряжение, необходимое для скольжения дислокации в совершенном кристалле (напряжение Пайерлса).

Расчет силы Пайерлса — очень сложная и до конца не решен­ная задача. Одна из основных трудностей состоит в том, что не­известны точное расположение атомов в ядре дислокации и точный закон изменения сил взаимодействия между соседними атом­ными плоскостями при сдвиге на одно межатомное расстояние. Метод анализа, созданный Пайерлсом и развитый Набарро, при синусоидальном законе для силы взаимодействия соседних сдвигаемых по отношению одна к другой атомных плоскостей дает следующее выражение для напряжения Пайерлса:

где G – модуль упругости при сдвиге;

μ – коэффициент Пуассона;

a – расстояние между соседними атомными плоскостями, в которых происходит скольжение;

b – межатомное расстояние в направлении скольжения.

Чем больше силы межатомной связи, характеристикой которых является модуль сдвига, тем больше τ_п. Критическое напряжение снижается с ростом соотношения 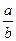. Для плоскостей и направле­ний с плотнейшей упаковкой это соотношение обычно наибольшее. Вот почему скольжение легче всего идет по плоскостям и направле­ниям плотнейшей упаковки.

В показатель степени выражения (67) входит важная харак­теристика — ширина дислокации . Следовательно:

Так как между сильно и слабо искаженными участками ре­шетки вокруг линии дислокации нет резкой границы, то понятие ее ширины условно. Под шириной дислокации принято понимать ширину области в плоскости скольжения и в направлении сколь­жения, в которой смещения атомов из равновесных положений со­вершенной решетки превышают половину максимального смеще­ния атомов [3]. Экспериментально ширина дислокаций не опреде­лена. Обычно считают, что у металлов ширина дислокации нахо­дится в пределах от двух до десяти межатомных расстояний.

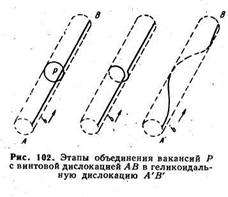
Весьма важно, что ширина дислокации стоит в показателе степени в выражении (68): небольшие изменения ее сильно ска­зываются на величине τ_п. Уменьшение силы Пайерлса с увели­чением ширины дислокации имеет простые физические основания. Краевая дислокация является нониусом, в котором п атомных плоскостей с одной стороны от плоскости скольжения противостоят (n+1) атомным плоскостям с другой стороны. При пере­мещении дислокации на одно межатомное расстояние b каждая из атомных плоскостей перемещается на 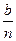. Поэтому необходимая для перемещения дислокации сила тем меньше, чем больше п, т. е. чем шире дислокация. На рис. 32, б (по сравнению с рис.32, а) прямо показано, что перемещение более широкой винтовой ди­слокации на один период решетки вправо происходит путем мень­ших перемещений атомов в области несовершенства.

Ширина дислокации зависит от природы сил межатомного взаимодействия. Доказывается, что в ковалентных кристаллах при направленных межатомных связях дислокации должны быть узкими. При ненаправленных межатомных связях (типичные ме­таллы) дислокации должны быть широкими.

Критическое касательное напряжение, обусловленное «тре­нием» в решетке, очень трудно не только рассчитать, но и экспе­риментально определить, так как действительный предел текучести зависит не только от силы Пайерлса, но и от других факто­ров, сильно препятствующих скольжению и не связанных с дей­ствием сил Пайерлса (см. § 43—46).

У типичных металлов с г. ц. к. решеткой, для которых харак­терна большая ширина дислокаций и соответственно небольшая сила Пайерлса, вклад этой силы в значение реального предела текучести очень мал. В переходных металлах с о. ц. к. решеткой сила Пайерлса высокая. По всей видимости это связано с тем, что в решетках таких металлов проявляется направленность меж­атомных связей и, следовательно, ширина дислокаций мала.

Теория предсказывает, что в кристалле, свободном от других дефектов, дислокация может скользить и при напряжениях меньше напряжения Пайерлса. Благодаря действию сил Пайерлса потен­циальная энергия дислокаций является периодической функцией ее положения в решетке (рис. 124). Минимальные значения по­тенциальной энергии (канавки потенциального рельефа) соот­ветствуют положениям дислокации вдоль направлений плотнейшей упаковки. Для перемещения дислокации из одной канавки в соседнюю требуется преодолеть потенциальный барьер, прило­жив напряжение Пайерлса.

Иная картина предполагается в случае, когда одна дислока­ция расположена в соседних канавках потенциального рельефа, т. е. имеет перегибы (см. рис. 124). Движение перегиба вдоль ли­нии дислокации может привести к последовательному (участок за участком) переходу всей дислокации в соседнее положение с минимумом энергии. Напряжение, требуемое для движения пе­региба параллельно направлению плотнейшей упаковки, очень мало (меньше напряжения Пайерлса). «Выбрасывание» полупетли в соседнюю канавку (образование двойного перегиба, см. рис. 124) происходит под действием термической активации, а дальнейшее расхождение перегибов в разные стороны — под действием очень малых приложенных напряжений.

Скорость скольжения дислокации v, движущейся вследствие образования двойных перегибов, зависит от частоты и, соответ­ственно энергии образования этих перегибов U_п:

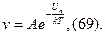
Таким образом, основная идея теории дислокаций — представ­ление о неодновременности протекания акта скольжения распро­страняется и на перемещение самой линии дислокации.

Дата добавления: 2014-01-05