
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Наращение по учетной ставке
|
|
|
|
Можно рассмотреть задачу, обратную банковскому дисконтированию. Пусть от учета капитала F по учетной ставке  за время
за время  была получена сумма
была получена сумма 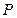 . Требуется определить величину F. Из формулы (2.18) получим
. Требуется определить величину F. Из формулы (2.18) получим
 (2.20)
(2.20)
Задачи такого типа возникают, например, при определении суммы, которую надо написать в векселе, если задана текущая величина долга.
Пример:
За вексель, учтенный за полтора года до срока по дисконтной ставке 8%, заплачено 2,2 тыс. тенге Определить номинальную величину векселя.
Поскольку  ;
;  ;
;  ; то из (2.20) получим
; то из (2.20) получим
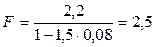 тыс. тенге
тыс. тенге
Так как 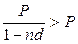 , то формула (2.20) отражает наращение капитала на основе простой учетной ставки
, то формула (2.20) отражает наращение капитала на основе простой учетной ставки  , и приращение
, и приращение 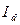 капитала вычисляется по формуле
капитала вычисляется по формуле
 (2.21)
(2.21)
что, конечно, представляет собой вычисление процентов "во 100" величины 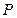 , т.е. по формуле (2.20) капитал наращивается процентами "во 100". Приращение
, т.е. по формуле (2.20) капитал наращивается процентами "во 100". Приращение 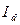 не пропорционально ни времени
не пропорционально ни времени  , ни ставке
, ни ставке  .
.
Величина  является множителем наращения. Этот множитель равен индексу роста капитала
является множителем наращения. Этот множитель равен индексу роста капитала 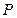 за время
за время  и является обратной величиной коэффициента дисконтирования.
и является обратной величиной коэффициента дисконтирования.
При 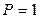 ,
,  из формулы (2.21) следует, что
из формулы (2.21) следует, что
 ,
,
т.е. множитель наращения  представляет собой сумму, например, рубля и его процентов за один год "во 100".
представляет собой сумму, например, рубля и его процентов за один год "во 100".
При наращении капитала на основе простой процентной ставки г капитал 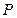 ежегодно увеличивается на одну и ту же величину
ежегодно увеличивается на одну и ту же величину  . При применении наращения на основе простой учетной ставки
. При применении наращения на основе простой учетной ставки  величина начисляемых процентов с каждым годом увеличивается. Пользуясь формулой (2.21), выпишем в явном виде приращение капитала
величина начисляемых процентов с каждым годом увеличивается. Пользуясь формулой (2.21), выпишем в явном виде приращение капитала 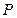 за каждый год.
за каждый год.
За первый год  капитал увеличится на величину
капитал увеличится на величину  .
.
За два года  капитал увеличится на величину
капитал увеличится на величину  , и, следовательно, его приращение за второй год составит:
, и, следовательно, его приращение за второй год составит:
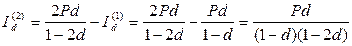 .
.
За три года капитал увеличится на величину  и, следовательно, его приращение за третий год составит:
и, следовательно, его приращение за третий год составит:
 и т.д.
и т.д.
Вообще за  -й год
-й год  капитал увеличится на величину:
капитал увеличится на величину:
 .
.
Из написанных равенств следует, что
 ,
, 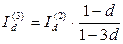 , …, т.е.
, …, т.е.  ,
,  .
.
И поскольку  , то
, то  . Очевидно, что
. Очевидно, что  .
.
Пример:
На капитал в 3 млн. тенге в течение 5 лет осуществляется наращение простыми процентами по учетной ставке 12%. Найти приращение первоначального капитала за каждый год и общую наращенную сумму.
Общая наращенная сумма определяется по формуле (2.20):
 млн. тенге. Приращение капитала
млн. тенге. Приращение капитала 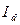 за пять лет составит величину:
за пять лет составит величину:  млн. тенге. Приращения за каждый год равны:
млн. тенге. Приращения за каждый год равны:
 млн. тенге;
млн. тенге;
 млн. тенге;
млн. тенге;
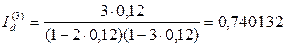 млн. тенге;
млн. тенге;
 млн. тенге;
млн. тенге;
 млн. тенге
млн. тенге
С целью проверки просуммируем полученные величины:
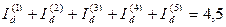 млн. тенге, т.е. как и должно быть, получили
млн. тенге, т.е. как и должно быть, получили 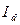 .
.
Формулы (2.20) и (2.1) показывают, что простая учетная ставка  дает более быстрый рост, чем такая же по величине простая процентная ставка
дает более быстрый рост, чем такая же по величине простая процентная ставка  .
.
Это легко обосновать математически. Пусть  . Обозначим
. Обозначим
 ,
,

При  справедливо неравенство
справедливо неравенство 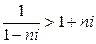 , а тогда и
, а тогда и  .
.
Графически взаимосвязь между  и
и  выглядит таким образом (рис 4):
выглядит таким образом (рис 4):
|

Нетрудно заметить, что прямая  является касательной к ветви гиперболы
является касательной к ветви гиперболы  при
при  .
.
Формулу (2.20) можно применять только при  , так как при
, так как при  она приводит к абсурду. Так, при
она приводит к абсурду. Так, при 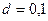 и
и 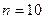 (лет) получим
(лет) получим  , а при
, а при  получим
получим  , что не имеет смысла.
, что не имеет смысла.
Найдем соотношение между годовыми процентными ставками  и
и 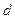 , обеспечивающими через период времени
, обеспечивающими через период времени  получение одной и той же наращенной величины
получение одной и той же наращенной величины 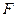 из начального капитала
из начального капитала 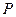 .
.
Поскольку 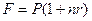 и
и 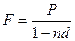 , то из равенства
, то из равенства  путем несложных алгебраических преобразований получим
путем несложных алгебраических преобразований получим
 (2.22)
(2.22)
Пусть  , тогда из (2.22) следует
, тогда из (2.22) следует

Таким образом, ставка  численно равна наращенной сумме, получаемой через год из капитала величиною
численно равна наращенной сумме, получаемой через год из капитала величиною 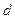 , инвестированного под простые проценты
, инвестированного под простые проценты  . В свою очередь,
. В свою очередь, 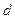 является приведенной стоимостью величины
является приведенной стоимостью величины  , соотнесенной к началу года.
, соотнесенной к началу года.
Записав 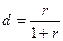 , можно сказать, что
, можно сказать, что 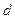 является процентами "на 100" одной денежной единицы согласно ставке
является процентами "на 100" одной денежной единицы согласно ставке  . Аналогичным образом, так как
. Аналогичным образом, так как 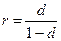 , то
, то  является процентами "во 100" одной денежной единицы согласно ставке
является процентами "во 100" одной денежной единицы согласно ставке 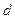 .
.
Рассмотрим с этих позиций показатели, введенные в первом разделе первой главы, смысл которых можно объяснить аналогичным образом, как для  и
и 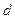 .
.
Умножая обе части равенства (2.22) на  и обозначая
и обозначая  ,
, 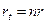 , получим
, получим

откуда следуют равенства (1.3). Иначе говоря, 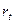 является наращенной за время t величиной для
является наращенной за время t величиной для  , a
, a  представляет собой современное значение величины
представляет собой современное значение величины 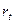 , приведенной к начальному моменту.
, приведенной к начальному моменту.
Ставки 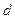 и
и  , связанные между собой соотношением (2.22), называются эквивалентными, так как они приводят к одинаковому финансовому результату (выполнение этого требования и позволило получить (2.22)). Согласно (2.22) соотношения между процентной ставкой
, связанные между собой соотношением (2.22), называются эквивалентными, так как они приводят к одинаковому финансовому результату (выполнение этого требования и позволило получить (2.22)). Согласно (2.22) соотношения между процентной ставкой  и эквивалентной ей учетной ставкой
и эквивалентной ей учетной ставкой 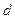 имеют вид:
имеют вид:
 и
и 
Пример:
Найти учетную ставку, эквивалентную простой процентной ставке 19%, при наращении капитала за год.
Поскольку 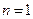 ,
,  , то
, то 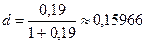 , или
, или  . Таким же образом, учет за год по учетной ставке 16% приносит такой же доход, как наращение простыми процентами по ставке 19%.
. Таким же образом, учет за год по учетной ставке 16% приносит такой же доход, как наращение простыми процентами по ставке 19%.
Когда время измеряется в днях  , то
, то 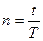 , где
, где 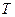 - временная база, равная количеству дней в году (360 или 365, 366). Если для ставок
- временная база, равная количеству дней в году (360 или 365, 366). Если для ставок  и
и 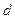 используется одна и та же временная база
используется одна и та же временная база 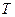 , то (2.22) примет вид
, то (2.22) примет вид  , откуда
, откуда
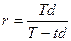 и
и 
Если при начислении процентов по ставке  используется временная база
используется временная база  , а при учете по ставке
, а при учете по ставке 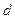 - временная база
- временная база  , то из равенства
, то из равенства
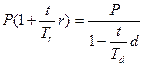
следует 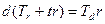 . Отсюда, в частности, при
. Отсюда, в частности, при  и
и  получим
получим
 и
и 
Пример:
Банк учитывает вексель за 210 дней до срока по учетной ставке 12%, используя временную базу в 360 дней. Определить доходность такой операции по процентной ставке при временной базе, равной 365.
Согласно последним формулам  , или
, или  .
.
Учетная ставка может иногда меняться во времени. Пусть на период 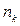 установлена учетная ставка
установлена учетная ставка 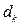 (заметим, что индекс
(заметим, что индекс 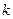 в обозначении ставки
в обозначении ставки 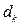 означает в данной ситуации просто номер ставки, а не время согласно ранее принятым нами соглашениям). Тогда дисконт за этот период равен величине
означает в данной ситуации просто номер ставки, а не время согласно ранее принятым нами соглашениям). Тогда дисконт за этот период равен величине  . Если таких периодов
. Если таких периодов 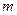 (т.е.
(т.е.  ), то дисконт
), то дисконт  за время
за время  (считая, что все периоды и, следовательно, ставки измеряются в одних и тех же соответствующих единицах) определяется по формуле
(считая, что все периоды и, следовательно, ставки измеряются в одних и тех же соответствующих единицах) определяется по формуле
 ,
,
следовательно,
 ,
,
откуда получаем
 (2.23)
(2.23)
Если  , т.е. на весь период соглашения установлена постоянная ставка, то
, т.е. на весь период соглашения установлена постоянная ставка, то
 ,
,
и мы, естественно, из (2.23) получаем формулу (2.20). Если же 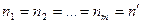 , т.е. все периоды равны между собой, то
, т.е. все периоды равны между собой, то
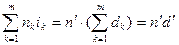 ,
,
и опять получаем (2.20), заменяя все учетные ставки их суммой  .
.
Сделаем некоторые заключения о способах наращения капитала и способах его учета, соотнеся их с методами вычисления процентов.
Возможны два способа наращения капитала: наращение процентами "со 100" (формулы (2.1), (2.2)) и наращение процентами "во 100" (формулы (2.20), (2.21)).
В первом случае происходит суммирование первоначального капитала и процентного дохода (в соответствии с процентной ставкой  ), причем начисление процентов осуществляется в конце расчетного периода. Такой способ начисления процентов по процентной ставке г называется декурсивным (последующим), а саму ставку
), причем начисление процентов осуществляется в конце расчетного периода. Такой способ начисления процентов по процентной ставке г называется декурсивным (последующим), а саму ставку  иногда называют ссудным процентом.
иногда называют ссудным процентом.
Во втором случае проценты начисляются в начале расчетного периода на сумму погашения долга в соответствии с учетной ставкой 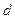 . Такой способ начисления процентов называется антисипативным (предварительным). Вообще наращение процентами "во 100" (антисипативное) используется, как правило, при учете долговых обязательств и при выдаче ссуд, а также в периоды высокой инфляции.
. Такой способ начисления процентов называется антисипативным (предварительным). Вообще наращение процентами "во 100" (антисипативное) используется, как правило, при учете долговых обязательств и при выдаче ссуд, а также в периоды высокой инфляции.
Если, например, внести в банк 4 тыс. тенге на полгода под 10% годовых, то через полгода можно получить свои 4 тыс. тенге вместе с 0,2 тыс. тенге, являющимися процентами "со 100", т.е. всего 4,2 тыс. тенге (декурсивное начисление). Если же обратиться в банк за ссудой в 4 тыс. тенге на полгода под 10%, то банк удержит проценты за весь срок ссуды (0,2 тыс. тенге) сразу, т.е. будет выдано на самом деле 3,8 тыс. тенге, а через полгода банк получит 4 тыс. тенге. Следовательно, банк получит 3,8 тыс. тенге с процентами на эту сумму "во 100" (антисипативное начисление).
Возможны два способа учета капитала: учет из процентов "со 100" (формулы (2.17), (2.18)) и учет из процентов "на 100" (формулы (2.15), (2.16)).
Таким образом, можно сказать, что  является ставкой наращения процентами "со 100" и ставкой учета процентами "на 100", a
является ставкой наращения процентами "со 100" и ставкой учета процентами "на 100", a 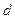 является ставкой учета процентами "со 100" и ставкой наращения процентами "во 100".
является ставкой учета процентами "со 100" и ставкой наращения процентами "во 100".
Как мы видели, проценты "со 100" находят в прямых задачах, а проценты "на 100" и "во 100" - в обратных задачах.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 6018; Нарушение авторских прав?; Мы поможем в написании вашей работы!