Наращение сложными процентами

Тема 4. СЛОЖНЫЕ ПРОЦЕНТЫ

1. Наращение сложными процентами.

2. Внутригодовые процентные начисления.

3. Дисконтирование по сложной процентной ставке.

Для пояснения принципиальной разницы между простыми и сложными процентами рассмотрим такую ситуацию. Клиент положил в банк на несколько лет сумму, равную 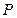, под про­стые проценты по ставке , причем счет можно закрыть в лю­бое время и происходит ежегодное декурсивное начисление процентов. Если клиент через два года закроет счет, то он полу­чит на руки .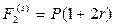

Но он может поступить и таким образом: через год закрыть счет, получив сумму 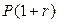, а затем положить эту сумму еще на год, осуществив тем самым операцию реинвестирования. Такое действие позволит ему в конце второго года получить

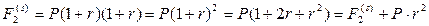
Величина 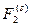больше 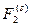на величину 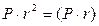, ко­торая представляет собой проценты, начисленные на проценты 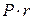, полученные за первый год. Еще значительнее будет раз­ница между суммой, полученной через 3 года при закрытии сче­та, и суммой, полученной в результате переоформления счета каждый год.

Ясно, что клиенту выгодно ежегодное переоформление счета. Поэтому с целью предотвращения такого рода действий и по­ощрения долгосрочных вкладов в коммерческой практике при­меняют сложные проценты.

Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с ис­ходной величины инвестированного капитала 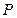(как для про­стых процентов), а с общей суммы, включающей также и ранее начисленные и не востребованные инвестором проценты. В этом случае происходит капитализация процентов, т.е. присое­динение начисленных процентов к их базе, и, следовательно, база, с которой начисляются проценты, все время возрастает. Таким образом, размер инвестированного капитала будет равен:

к концу первого года: ;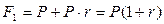

к концу второго года: ;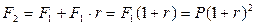

к концу -го года:

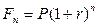(4.1)

Равенство (4.1) называется формулой наращения по сложным процентам или формулой наращения сложными процентами; множитель 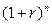- множителем наращения (accumulation factor) сложных процентов или мультиплицирующим множите­лем; - коэффициентом наращения, или сложным декурсивным коэффициентом.

Из (4.1) видно, что множитель наращения равен индексу рос­та суммы 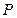за лет.

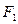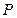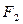Согласно формуле (4.1) наращение капитала происходит сложными процентами "со 100". Действительно, является суммой капитала и процентов "со 100". Величина является суммой капитала 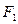(наращенного за один год из пер­воначального капитала 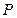) и процентов "со 100" по отношению к 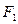и т.д.

Очевидно, последовательность 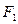,,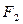..,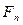представляет со­бой геометрическую прогрессию со знаменателем .

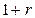В отличие от схемы простых процентов в данном случае приращение капитала

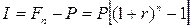(4.2)

не пропорционально ни сроку ссуды, ни ставке процента (есте­ственно, если ).

Заметим, что поскольку при начислении сложных процентов осуществляется реинвестирование, то формула (4.1) следует и из формулы (2.11), когда каждый период начисления процентов равен одному году (т.е. в формуле (2.11) полагаем ).

Пример:

Депозит в 200 тыс. тенге положен в банк на 4 года под 15% годовых. Найти наращенную сумму, если ежегодно начисляют­ся сложные проценты.

Применяя формулу (4.1), получим

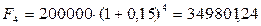тенге

Использование в расчетах сложного процента в случае мно­гократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начис­ления целесообразно снимать для потребления или использова­ния в других инвестиционных проектах или текущей деятель­ности.

Формула наращения по сложным процентам является одной из базовых формул в финансовых вычислениях, поэтому для удобства пользования значения множителя 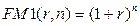, обеспечивающего наращение стоимости, табулированы для раз­личных значений и . Тогда фор­мула алгоритма наращения по схеме сложных процентов пере­писывается следующим образом:

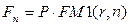(4.3)

Экономический смысл множителя 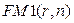состоит в сле­дующем: он показывает, чему будет равна одна денежная еди­ница (один рубль, один доллар, одна иена и т.п.) через перио­дов при заданной процентной ставке . При выводе формулы (4.1) предполагалось, что измеряется в годах, а является годовой процентной ставкой. Однако эту формулу можно при­менять и при других периодах начисления. Необходимо только следить за соответствием длины периода и процентной ставки. Сказанное должно быть учтено и при пользовании финансовы­ми таблицами. Так, если базовым периодом начисления процен­тов является квартал (месяц), то в расчетах должна использо­ваться квартальная (месячная) ставка.

Как и в случае начисления простых процентов, финансовое соглашение может предусматривать плавающие процентные ставки и при наращении по сложным процентам. Пусть 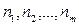- следующие друг за другом периоды и на период 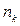установлена процентная ставка 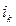. Тогда, учитывая капита­лизацию начисленных процентов при использовании схемы сложных процентов, наращенная сумма за время 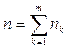(считая, что все периоды и, следовательно, процентные ставки измеряются в одних и тех же соответствующих единицах) опре­деляется по формуле

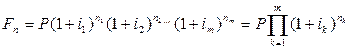(4.4)

Обозначим 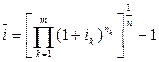, тогда (3.4) примет вид .

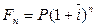Таким образом, в течение всего периода длитель­ностью можно установить сложную ставку 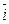, доставляющую такой же результат, как и переменные ставки, при этом для на­хождения наращенной суммы можно пользоваться формулой (4.1).

Если 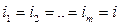, т.е. на весь период соглашения уста­новлена постоянная ставка, то из (4.4) получаем (4.1).

Естественно, формулой (3.4) можно пользоваться и в тех случаях, когда периоды выражены в различных единицах вре­мени. Необходимо только, чтобы размерность каждого периода 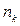была согласована с размерностью процентной ставки .

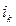Пример:

Предприниматель получил в банке ссуду в размере 25 тыс. тенге сроком на 6 лет на следующих условиях: для первого года процентная ставка равна 10% годовых, на следующие два года устанавливается маржа в размере 0,4% и на последующие годы маржа равна 0,7%. Найти сумму, которую предприниматель должен вернуть в банк по окончании срока ссуды.

Так как 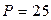, , , , 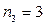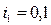; ; 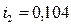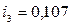, то по формуле (3.4):

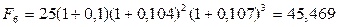тыс. тенге

Такая же величина наращенной суммы получается, если в те­чение 6 лет начисляются сложные проценты по ставке

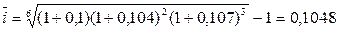, или .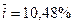

Достаточно обыденными являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться с помощью сле­дующих методов:

- по схеме сложных процентов:

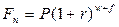(4.5)

- по смешанной схеме (используется схема сложных про­центов для целого числа лет и схема простых процен­тов - для дробной части года):

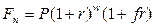(4.6)

где 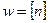- целое число лет (квадратной скобкой обозначена целая часть числа);

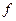- дробная часть года ;

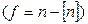Пример:

Банк предоставил ссуду в размере 10 тыс. тенге на 30 месяцев под 30% годовых на условиях ежегодного начисления процен­тов. Какую сумму предстоит вернуть банку по истечении срока?

В данном случае , , .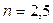

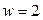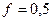По формуле (3.5): 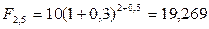тыс. тенге. По формуле (3.6): тыс. тенге

Таким образом, в условиях задачи смешанная схема начисле­ния процентов более выгодна для банка.

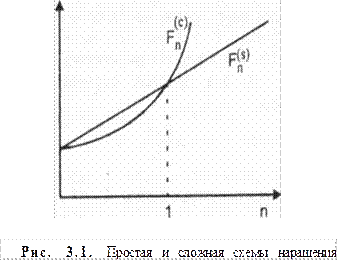
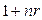Как же соотносятся величины наращенных сумм при начис­лениях по схеме простых и по схеме сложных процентов? Это чрезвычайно важно знать при проведении финансовых опера­ций. Все зависит от величины . Сравним множители нараще­ния по простым и сложным процентам, т.е. сравним и 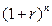. Очевидно, что при 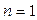эти множители совпадают и равны 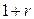. Можно доказать, что при любом справедливы неравенства:

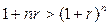, если ;

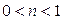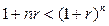, если .

Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:

более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);

более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

обе схемы дают одинаковые результаты при продолжи­тельности периода 1 год и однократном начислении про­центов.

Отсюда, в частности, следует, что наращенная сумма будет больше при использовании смешанной схемы (формула (3.6)), чем при использовании схемы сложных процентов (формула (3.5)), что и наблюдали в предыдущем примере. Можно пока­зать (используя ряды), что при малых наибольшая величина разности между (4.6) и (4.5) достигается при .

Рис.6. Простая и сложная схемы наращения капитала  

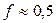Пример:

Рассчитать наращенную сумму с исходной суммы в 1 млн. тенге при размещении ее в банке на условиях начисления про­стых и схемы сложных процентов, если: а) годовая ставка 20%; б) периоды наращения: 30 дней, 90 дней, 180 дней, 1 год, 5 лет, 10 лет. Полагать год равным 360 дням.

Результаты расчетов имеют следующий вид:

(млн тенге)

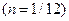
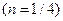
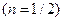
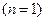
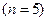
Схема начисления	30 дней	90 дней	180 дней	1 год	5 лет	10 лет
Простые проценты	1,0167	1,05	1,10	1,20	2,0	3,0
Сложные проценты	1,0153	1,0466	1,0954	1,20	2,4883	6,1917

Таким образом, если денежные средства размещены в банке на срок 90 дней (менее одного года), то наращенная сумма со­ставит: при использовании схемы простых процентов - 1,05 млн. тенге; при использовании схемы сложных процентов - 1,0466 млн. тенге. Следовательно, более выгодна первая схема (разница - 3,4 тыс. тенге). Если срок размещения денежных средств превышает один год, ситуация меняется диаметрально - более выгодна схема сложных процентов, причем наращение в этом случае идет очень быстрыми темпами. Так, при ставке в 20% годовых при использовании схемы простых процентов за 5 лет происходит удвоение исходной суммы, а при использовании схемы сложных процентов за 5 лет исходная сумма увеличива­ется почти в 2,5 раза. Еще большую разницу между наращен­ными суммами мы видим через 10 лет.

Найдем в общем виде время, необходимое для увеличения первоначальной суммы 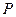в 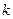раз при начислении простых и сложных процентов. Так как в обоих случаях множители нара­щения равны 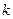, то для простых процентов из равенства 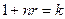получаем

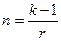, (4.7)

а для сложных процентов из равенства 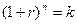получаем

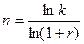(4.8)

Из этих формул можно найти период, за который происходит удвоение первоначальной суммы при одинаковой ставке про­стых и сложных процентов. Полагая в (4.7) и (4.8) 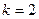, соот­ветственно получим

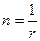(для простых процентов),

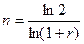(для сложных процентов).

В практических расчетах для наглядной и быстрой оценки эффективности предлагаемой ставки наращения при реализации схемы сложных процентов пользуются приблизительным расче­том времени, необходимого для удвоения инвестированной суммы, известным как "правило 72-х". Это правило заключается в следующем: если - процентная ставка, выраженная в про­центах, то 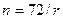представляет собой число периодов, за ко­торое исходная сумма приблизительно удвоится. Это правило хорошо срабатывает для небольших значений (до 20%). Так, если годовая ставка , то 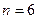годам. Подчеркнем, что здесь речь идет о периодах начисления процентов и соответст­вующей данному периоду ставке, а именно: если базовым пе­риодом, т.е. периодом наращения, например, является половина года, то в расчете должна использоваться полугодовая ставка. Следует также обратить внимание на то обстоятельство, что хотя в большинстве финансовых расчетов процентная ставка берется в десятичных дробях, в формуле алгоритма "правила 72-х" ставка взята в процентах.

Существуют и другие правила, с помощью которых быстро рассчитывают срок удвоения первоначального капитала для конкретной ставки. В литературе можно встретить "правило 70": 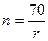и аналогичное "правило 71". Отметим также "правило 69": 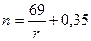. Например, при годовой ставке по правилам "70", "71" и "69" соответственно получим:

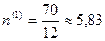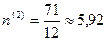года, года; 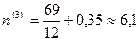года. Так как все перечисленные правила дают приблизительные значения, то, естественно, получаем расхождение в сроках. Если же воспользоваться точной формулой, то получим

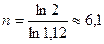года.

В случае нецелого числа лет кроме схемы сложных процен­тов и смешанной схемы (формулы (4.5) и (4.6)) возможны и дру­гие методы начисления процентов. Приведем эти методы и сравним их между собой.

Можно использовать схему сложных процентов для целого числа лет, взяв это число с избытком, и затем полученную сум­му учесть "на 100" из простых процентов за лишнее время, до­бавленное для достижения целого числа лет. Таким образом, если 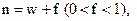то добавляем время 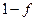и получа­ем целое число лет 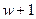. Наращенная сумма находится по формуле

(4.9)

Если же сумму 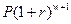учесть простыми процентами "со 100" за лишнее время, то наращенная сумма определяется фор­мулой

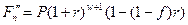(4.10)

Можно использовать схему сложных процентов для цело­го числа лет и затем полученную сумму нарастить простыми процентами "во 100" за дробную часть года, т.е. применить формулу

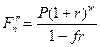(4.11)

Конечно, (4.11) можно применить, если 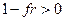. Поскольку в этом случае 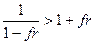, то наращение по формуле (4.11) дает больший результат, чем по смешанной схеме (4.6).

Так как 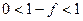, то справедливо неравенство 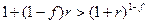, которое равносильно при умножении обеих его частей на 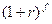неравенству 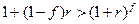, т.е. справедливо . Таким образом, наращение по формуле (4.9) дает меньший результат, чем по схеме сложных процентов (4.5). А поскольку 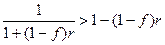, то (4.10) доставляет меньшую сумму, чем (4.9).

Следовательно, наращенные суммы расположатся в порядке убывания, если их вычислять последовательно по формулам: (4.11), (4.6), (4.5), (4.9), (4.10).

Дата добавления: 2014-01-05