Внутригодовые процентные начисления

Пример

Кредит в размере 2 тыс. тенге выдан на 33 месяца по ставке 16% годовых. Определить сумму долга на конец срока.

Если вычислять наращенные суммы последовательно по формулам, номера которых приведены перед формулировкой примера, то получим следующие результаты ; ; ; ):

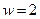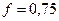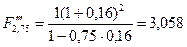тыс. тенге;

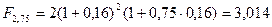тыс. тенге (смешанная схема);

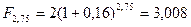тыс. тенге (схема сложных процентов);

тыс. тенге;

тыс. тенге

Действительно наблюдаем убывание величин наращенных сумм.

На практике капитализация процентов часто происходит не­сколько раз в году - по полугодиям, ежеквартально, ежемесяч­но и даже ежедневно. Например, такие ситуации нередко преду­сматриваются условиями в депозитных договорах, в соглашени­ях на получение кредита, в контрактах, оговаривающих выплату дивидендов, и т.п.

При начислении сложных процентов несколько раз в году пользуются формулой (4.1), понимая под число периодов начисления, а под - процентную ставку за период. Однако в финансовых соглашениях, как правило, указывается не ставка за период, а годовая процентная ставка и одновременно определяется количество периодов начисления. С этих позиций преобразуем формулу (4.1).

Итак, пусть заданы количество 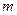начислений в году и годовая процентная ставка, которую обозначим через (при помощи верхнего индекса 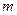указываем, сколько раз в течение года происходит наращение). В этом случае длительность периода наращения равна 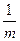годам. Годовая процентная ставка называется номинальной, если соответствующая процентная ставка за период 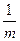находится из равенства 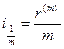. Заметим, что такое с нашей точки зрения удачное обозначение номинальной ставки придумано не нами. Аналогичное, только с индексом внизу, использовал, например, Н.С. Лунский.

В этих обозначениях формула (4.1) для нахождения наращенного капитала за лет при 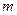- кратном начислении процентов в год примет вид:

(4.12)

где 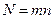- количество периодов начисления процентов за лет.

Конечно, (4.1) можно рассматривать в качестве частного случая (4.12) при .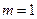

С целью упрощения записи в дальнейшем, если не возникает недоразумений, индекс 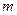у номинальной процентной ставки будем периодически опускать и писать просто , однако при этом помня о количестве начислений процентов за базовый период.

Пример:

В банк вложены деньги в сумме 5 тыс. тенге на два года с полугодовым начислением процентов под 20% годовых. В этом случае начисление процентов производится четыре раза по ставке 10% (20%: 2), а схема возрастания капитала будет иметь вид:

Период	Сумма, с кото-рой идет начисление	Коэффициент наращения	Сумма к концу периода
6 месяцев	5,0	х 1,10	= 5,5
12 месяцев	5,5	х 1,10	= 6,05
18 месяцев	6,05	х 1,10	= 6,655
24 месяца	6,655	х 1,10	= 7,3205

Если пользоваться формулой (4.12), то

, , , ,

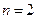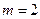следовательно,

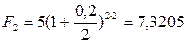тыс. тенге

Пример:

В условиях предыдущего примера проанализировать, изменится ли величина капитала к концу двухлетнего периода, если проценты будут начисляться ежеквартально.

В этом случае начисление будет производиться восемь раз 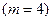по ставке 5% (20%: 4), а сумма к концу двухлетнего периода составит:

тыс. тенге

Таким образом, можно сделать несколько простых практических выводов:

- при начислении сложных процентов: 12% годовых не эквивалентно 1% в месяц (эта ошибка очень распространена среди начинающих бизнесменов);

- чем чаще идет начисление по схеме сложных процентов, тем больше итоговая накопленная сумма.

Заметим, что для простых процентов такие выводы не верны. Покажем это. В формуле наращения по простым процентам уменьшим период начисления в 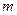раз. Тогда вместо надо взять процентную ставку , а вместо - количество периодов начисления процентов, равное . Вычисляем наращенную сумму

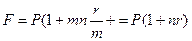
и убеждаемся, что она не изменяется. Приведенное свойство является одним из характерных свойств наращения по простым процентам. Например, наращение простыми процентами ежегодно по ставке 10% годовых дает тот же результат, что и ежеквартальное наращение простыми процентами по ставке 2,5% за квартал. При наращении по сложным процентам ежеквартальное начисление доставляет больший результат, чем ежегодное.

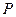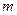Из формулы (4.12) можно найти период , за который сумма при - кратном начислении процентов в год по ставке возрастет до величины 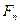. Решая (4.12) как уравнение относительно неизвестного , получим формулу:

(4.13)

которая пр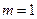и и примет вид:

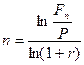(4.14)

что нетрудно получить и из равенства (4.1)

Аналогичным образом, решая (4.12) относительно , получим:

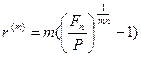
и при :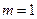

Пример:

На вклад начисляются ежемесячно сложные проценты по номинальной годовой процентной ставке 16%. За какой срок первоначальный капитал утроится? Как изменится результат, если сложные проценты начисляются ежегодно?

Полагая , , 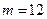и используя (4.13), получим:

года.

При ежегодном начислении процентов применяем формулу (4.14) или (4.13) при :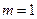

года.

Пример:

Вкладчик хотел бы за 5 лет удвоить сумму, помещаемую в банк на депозит. Какую годовую номинальную процентную ставку должен предложить банк при начислении сложных про­центов каждые полгода?

Так как , , 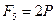, 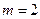то

,

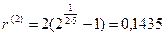т.е. ставка должна быть не менее 14,35%.

Заметим, что, применяя в данном случае "правило 72-х" в определенном смысле наоборот - для нахождения процентной ставки, получим 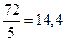, что не сильно отличается от 14,35%.

Возможны финансовые контракты, в которых начисление процентов осуществляется по внутригодовым подпериодам, а продолжительность общего периода действия контракта не рав­на целому числу подпериодов. В этом случае возможно исполь­зование схем:

а) схема сложных процентов:

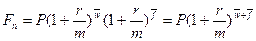(4.15)

б) смешанная схема:

(4.16)

где 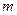- количество начислений в году;

- годовая ставка;

- целое число подпериодов в годах (, напомним, что в данном случае квадратные скобки обозначают целую часть числа);

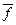- дробная часть подпериода ();

.

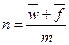Формулы (4.5) и (4.6) являются частными случаями соответ­ственно формул (4.15) и (4.16) при 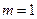. Обратим внимание также, что при 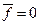формулы (4.15) и (4.16) совпадают между собой и с формулой (4.12).

Конечно, кроме схем (4.15) и (4.16) в принципе возможно и использование схем, аналогичных (4.9) - (4.11).

Пример:

Банк предоставил ссуду в размере 120 тыс. тенге на 27 меся­цев (т.е. 9 кварталов, или 2,25 года) под 16% годовых на услови­ях единовременного возврата основной суммы долга и начис­ленных процентов. Проанализировать, какую сумму предстоит вернуть банку при различных вариантах и схемах начисления процентов: а) годовое; б) полугодовое; в) квартальное.

Дата добавления: 2014-01-05