
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценка качества подбора уравнения
|
|
|
|
Оценка качества модели
Рассмотрим множественную регрессию, которую в общем виде можно записать следующим образом:
|
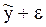 ,
,
где y – результативный признак;
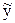 = f(x1, x2, …, xm) – уравнение регрессии;
= f(x1, x2, …, xm) – уравнение регрессии;
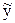 - значение результативного признака, рассчитанное по уравнению регрессии;
- значение результативного признака, рассчитанное по уравнению регрессии;
x1, x2, …, xm – признаки-факторы (m – число таких факторов);
ε – регрессионный остаток.
Уравнение регрессии объясняет вариацию результативного признака не полностью, а лишь частично; остается необъясненный остаток ε. Чем лучше в регрессионном уравнении подобрана функция f(X), отражающая регрессионную зависимость, тем меньше будут фактические значения показателя y отличаться от расчетных 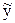 , т.е. тем меньше будет регрессионный остаток.
, т.е. тем меньше будет регрессионный остаток.
Приближение расчетных оценок к фактическим называют аппроксимацией, и чем они ближе, тем лучше построенное уравнение аппроксимирует реальный показатель.
Для оценки качества аппроксимации, т.е. качества подбора уравнения, рассчитывают ряд показателей.
Наиболее простой из них – абсолютная ошибка аппроксимации, т.е. разница между фактическим и расчетным значением результативного признака. Ее рассчитывают отдельно для каждого i-го наблюдения по формулам yi -  = εi. Если отнести ее по модулю к фактическому значению, можно получить относительную ошибку аппроксимации, которую обычно выражают в процентах:
= εi. Если отнести ее по модулю к фактическому значению, можно получить относительную ошибку аппроксимации, которую обычно выражают в процентах:  . Для расчета средней относительной ошибки эту величину суммируют по всем наблюдениям (пусть число наблюдений равно n) и делят на число наблюдений:
. Для расчета средней относительной ошибки эту величину суммируют по всем наблюдениям (пусть число наблюдений равно n) и делят на число наблюдений:  . Качество модели можно считать хорошим, если средняя относительная ошибка не превышает некоторого изначально заданного значения. Обычно берут 5-10%.
. Качество модели можно считать хорошим, если средняя относительная ошибка не превышает некоторого изначально заданного значения. Обычно берут 5-10%.
Более полную информацию об оценке полученного уравнения можно получить с помощью дисперсионного анализа, который предусматривает расчет общей, объясненной и остаточной дисперсий.
Общая дисперсия представляет собой дисперсию значений результативного признака и рассчитывается по формуле:
|

где n – число наблюдений;
y1, y2, … yn – значения результативного признака;
 - его среднее значение.
- его среднее значение.
Следует отметить, что общая дисперсия, рассчитанная по этой формуле, представляет собой не дисперсию выборки значений, а оценку дисперсии генеральной совокупности. В математической статистике доказывается, что если число элементов генеральной совокупности достаточно велико, то для получения несмещенной оценки ее дисперсии сумму квадратов отклонений от среднего делят не на число слагаемых n, а на число степеней свободы.
Для определения числа степеней свободы необходимо провести рассуждения о том, сколько единиц из всей совокупности наблюдений могут свободно варьировать относительно известного среднего. В данном случае это число наблюдений минус единица, т.е. (n – 1)[1].
Общая сумма квадратов отклонений. В формуле (3.2) величина представляет собой общую сумму квадратов отклонений результативного признака. Обозначим ее Qобщ. Ее называют также общей или полной вариацией.
представляет собой общую сумму квадратов отклонений результативного признака. Обозначим ее Qобщ. Ее называют также общей или полной вариацией.
Остаточная дисперсия – это показатель вариации результата под влиянием всех неучтенных в модели факторов, необъясненная часть дисперсии. Она представляет собой средний квадрат регрессионных остатков и рассчитывается по формуле:
|
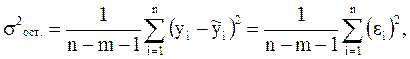
где  – значения результативного признака, рассчитанные по уравнению регрессии;
– значения результативного признака, рассчитанные по уравнению регрессии;
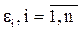 – значения регрессионного остатка;
– значения регрессионного остатка;
m - число факторов.
Можно доказать, что число степеней свободы для этой суммы квадратов тоже меньше числа наблюдений, причем меньше на число параметров регрессии. Для линейной регрессии число параметров равно (m +
+ 1): m коэффициентов при факторных переменных и свободный член. Поэтому в знаменателе из числа наблюдений n вычитается величина (m + 1).
Если бы имела место строгая функциональная зависимость между результатом и учтенными факторами, то регрессионные остатки всегда равнялись бы нулю. Тогда и остаточная дисперсия была бы равна нулю. Однако на практике такой ситуации обычно не встречается.
Остаточная сумма квадратов отклонений. В формуле (3.3) величина представляет собой остаточную сумму квадратов отклонений результативного признака. Обозначим ее Qост. Ее называют также остаточной вариацией.
представляет собой остаточную сумму квадратов отклонений результативного признака. Обозначим ее Qост. Ее называют также остаточной вариацией.
Объясненная дисперсия (факторная дисперсия) – это показатель вариации результата под влиянием тех факторов, которые учтены в регрессионной модели. Она представляет собой средний квадрат разностей между значениями результативного признака, рассчитанными по уравнению регрессии, и средним фактическим значением этого признака. Она рассчитывается по формуле:
|
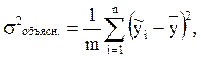
Число степеней свободы при расчете этого показателя равно числу параметров регрессии минус единица. Поэтому в знаменателе формулы стоит величина ((m + 1) – 1) = m.
Объясненная сумма квадратов отклонений. В формуле (3.4) величина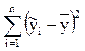 представляет собой объясненную сумму квадратов отклонений. Обозначим ее Qобъясн.. Ее называют также объясненной или факторной вариацией.
представляет собой объясненную сумму квадратов отклонений. Обозначим ее Qобъясн.. Ее называют также объясненной или факторной вариацией.
Дисперсия на одну степень свободы. Дисперсию, рассчитанную по формулам (3.2)-(3.4) называют также дисперсией на одну степень свободы [Елисеева И.И., Курышева С.В., Костеева Т.В. и др. Эконометрика: Учебник. – М.: Финансы и статистика, 2001. – 344 с.], поскольку в знаменателе этих формул из общего числа слагаемых вычитают число слагаемых, которые не могут свободно варьировать.
Следует отметить, что число степеней свободы в знаменателе формул расчета общей, объясненной и остаточной дисперсий подчиняется следующему правилу: для общей дисперсии оно равно сумме двух остальных. В самом деле, n - 1 = m + (n – m – 1).
Еще раз отметим, что в формулах (3.2)-(3.4) число степеней свободы зависит от числа наблюдений и от вида уравнения регрессии (им определяется число параметров).
|
Qобщ. = Qобъясн. + Qост..
Коэффициент детерминации. Отношение объясненной суммы квадратов к общей носит название коэффициента детерминации. Он рассчитывается как отношение объясненной суммы квадратов к общей по формуле:
|
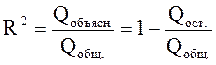
Коэффициент детерминации показывает, какая доля вариации результативного признака объясняется построенным уравнением регрессии. Он может принимать значения от нуля до единицы (ноль – если связь отсутствует, и единица – если вариация результата объяснена полностью).
В самом деле, формула (3.6) представляет собой сравнение вариации теоретических значений результата относительно его средних значений (в числителе) и общей вариации фактических значений признака (в знаменателе). Иными словами, сравнивается объяснение значений результата с помощью уравнения регрессии с его объяснением линией  .
.
Практическая значимость этого коэффициента заключается в том, что с его помощью можно оценить качество подбора уравнения регрессии и сравнивать между собой различные варианты моделей. Чем ближе значение коэффициента детерминации к единице, тем выше качество модели.
Однако в случае множественной регрессии коэффициент детерминации может быть затруднительно использовать для оценки модели, потому что он увеличивается при добавлении новых признаков-факторов, хотя такое добавление отнюдь не всегда улучшает модель. Чтобы избежать этого, рассчитывают скорректированный коэффициент детерминации (поправленный, адаптированный) по формуле:
|

Скорректированный коэффициент может уменьшаться при введении в модель дополнительных факторов, если они не оказывают существенного влияния на результат (с ростом числа факторов m велчина  уменьшается по сравнению с R2).
уменьшается по сравнению с R2).
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1834; Нарушение авторских прав?; Мы поможем в написании вашей работы!