Оценка тесноты связи моделируемого показателя с факторами

Для оценки тесноты связи используются следующие основные показатели:

1) коэффициент ковариации;

2) коэффициент корреляции;

3) коэффициент детерминации.

Коэффициент ковариацииможет использоваться для оценки тесноты связи между двумя показателями. Его рассчитывают по формуле (n – число наблюдений; - средние значения x, y и x*y). К сожалению, использование этого коэффициента затрудняется тем, что он зависит от единиц измерения показателей x и y.

Коэффициент корреляции. Как уже упоминалось ранее, для оценки тесноты линейной связи между двумя показателями (обозначим их x и y) обычно используют коэффициент корреляции (коэффициент корреляции Пирсона), который рассчитывается по формуле 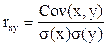(формула (1.4)).

В числителе этой формулы стоит коэффициент ковариации, а в знаменателе - произведение СКО переменных 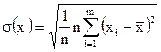и .

Преобразуем формулу (1.4), подставив в числитель и знаменатель формулы для расчета ковариации и СКО (а затем числитель и знаменатель умножим на n²):

(3.8)

Такую же формулу можно получить, если в выражение для расчета коэффициента детерминации (3.5) подставить 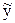= ax + b, а вместо a и b – выражения, полученные для этих параметров с помощью МНК ((2.4) и (2.6)); и извлечь корень квадратный из полученного выражения (алгебраические преобразования здесь не приводятся). Таким образом[2], можно убедиться, что для парной линейной регрессии коэффициент детерминации представляет собой не что иное, как квадрат линейного коэффициента корреляции. Соответственно, в этом случае для расчета коэффициента детерминации можно использовать формулу (3.9), а модуль коэффициента корреляции рассчитать по формуле (3.10):

(3.9)

(3.10)

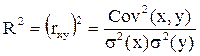
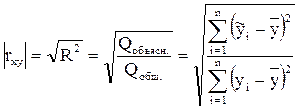
Из формулы (1.4) следует, что коэффициент корреляции может равняться нулю тогда и только тогда, когда числитель этой формулы (ковариация признаков) равен нулю. В этом случае коэффициент детерминации тоже равен нулю, и линейная связь между переменными отсутствует.

Таким образом, оба коэффициента могут служить для оценки тесноты связи: чем они ближе по модулю к единице, тем теснее связь. Если их модули равны единице, то связь функциональная. Но коэффициент детерминации не показывает направленность связи, так как всегда неотрицателен (от 0 до 1). Коэффициент линейной корреляции изменяется от (-1) до 1, и его отрицательное значение говорит об отрицательной корреляции (чем больше x, тем меньше y), а положительное – о положительной (x и y уменьшаются или растут вместе).

Коэффициент множественной корреляции может рассматриваться в качестве оценки тесноты связи между результатом и всеми факторами в случае множественной регрессии. Он рассчитывается по формуле, аналогичной формуле (3.10):

(3.11)

Его называют еще совокупным коэффициентом корреляции, индексом множественной корреляции или корреляционным отношением. Коэффициент множественной корреляции всегда не меньше наибольшего из парных коэффициентов корреляции:

(3.12)

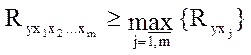
В общем случае индекс множественной корреляции может принимать значения от 0 до 1.

Корреляционное отношение может быть рассчитано по формуле (3.11) и для случая парной регрессии. Отметим, что в случае нелинейной связи его значение может отличаться от модуля парного коэффициента линейной корреляции. В отличие от линейного коэффициента корреляции, этот коэффициент позволяет измерить тесноту нелинейной связи между двумя переменными, но не позволяет определить ее направленность.

Для случая линейной множественной регрессии формула (3.11) может быть преобразована в формулы (1.7) или (1.18).

Поле корреляции

Наглядно проверить полученные результаты можно с помощью поля корреляции (диаграммы рассеяния), которое представляет собой точечный график, отражающий исходные данные для построения уравнения регрессии. Для парной регрессии он представлен на рисунке 3.1. По горизонтальной оси откладываются значения признака-фактора, а по вертикальной – результата. В виде прямой изображена линия регрессии. Чем ближе к этой линии лежат точки, соответствующие наблюдениям (эмпирические), тем теснее связь. Если связь строго линейная, то все они будут лежать непосредственно на этой прямой.

Поле корреляции может также использоваться при выборе формы аналитической зависимости, которая не обязательно должна быть линейной. Иногда при этом вместо эмпирических значений фактора и результата один из них или оба измеряют в отклонениях от средних значений, т.е. центрируют (вместо х берут , а вместо y - ).

Дата добавления: 2014-01-05