Предпосылки метода наименьших квадратов

Классический метод наименьших квадратов, лежащий в основе регрессионного анализа, предъявляет довольно жесткие требования к базе данных и свойствам полученных случайных остатков:

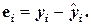
Должны выполняться ряд условий (предпосылки) метода наименьших квадратов.

Пусть выполнена основная предпосылка эконометрического анализа, т.е. моделируемую случайную величину Y можно разбить на две части объясненную и случайную:

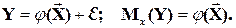
Перечислим предпосылки классического метода наименьших квадратов.

1). Зависимая переменная Y _i и возмущения E _i – это случайные величины, а вектор объясняющих переменных Х _i – неслучайный (детерминированный).

2). Математическое ожидание возмущений E _i равно 0:

M[E _i ]=0

3). Дисперсия возмущений E _i (дисперсия зависимой переменной Y _i) постоянна:

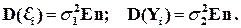(3.12)

где Еn – матричная единица.

Это условие называется гомоскедастичностью или равноизменчивостью возмущения E _i (зависимой переменной Y _i). На рисунке 3.1. показан случай нарушения свойства гомоскедастичности: 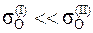, т.е. для разных диапазонов изменения х дисперсия существенно изменяется (зависит от х).

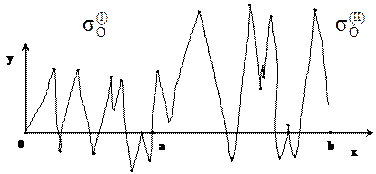
4). Возмущения E _i и E _j (или наблюдение Y _i и Y _j) не корректированы:

M(E _i ·E _j)= 0; i ¹ j (3.13)

5). Ранг матрицы плана X_[Nxn] должен быть не более числа опытов N:

r=k < N,

где, k – число членов регрессии. Ранг r равен числу линейно независимых столбцов матрицы X.

6). Возмущения E _i (или зависимая переменная Y _i) есть нормально распределенная случайная величина

E~N(0;s²E_n). (3.14)

При выполнении всех предпосылок 1…5 и 6 модель называется классической нормальной регрессионной моделью.

Замечание 1: Формально уравнение регрессии можно построить и без предпосылки s о нормальном ЗР? возмущений E _i. Однако при этом модель не имеет практического смысла, поскольку невозможно оценить:

- адекватность;

- точность;

- доверительные интервалы оценок коэффициентов и Y.

В этих операциях используется НЗР? (критерий Стьюдента)

Замечание 2: Для получения адекватного, хорошего интерпретируемого (с возможностью раздельной оценки вклада каждого фактора) уравнения регрессии с необходимой точностью требуется выполнение еще одной седьмой предпосылки.

7). Отсутствие мультиколлинеарности.

Мультиколлениарность – это наличие линейной корреляции объясняющих переменных между собой.

Предпосылки метода наименьших квадратов проверяются как соответствующие статистические гипотезы.

Дата добавления: 2014-01-05