Разностные уравнения с лаговыми пременными

Авторегрессионная модель скользящей средней.

Авторегрессионные модели.

1. Назначение:

1). Случай, когда для обычной регрессии нарушаются предпосылки регрессионного анализа.

- гетероскедантичность;

- автокоррелированность остатков;

Переход к авторегрессии может значительно улучшить ситуацию.

2). Хорошо описывает колебательные процессы, на пример сезонные колебания.

В моделях авторегрессии вместо регрессора t выступают лаговые переменные

Лаговые переменные – это переменные, объясняющие моделирующую величину Y с некоторым запаздыванием. Второе отличие от классических временных рядов – то, что объясняющие переменные – случайные величины (по своему смыслу).

AR(p) – порядка p.

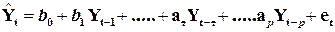. (4.7)

т.е. - есть линейная комбинация значений Y в предыдущие моменты времени;

Здесь Y(t-1),….Y(t- p) – лаговые независимые переменные (переменные с запаздыванием);

AR(1) – это Марковский случайный процесс (зависимость только от скорости - первых разностей):

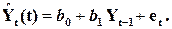(4.8)

Пример: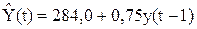

«Moving average» - скользящая средняя.

ARMA - авторегрессионная модель скользящей средней.

Замечание:

Не следует путать авторегрессионную модель скользящей средней с методом простой скользящей средней при сглаживании временных рядов. В правой части этой модели стоят лаговые переменные по Y и e:

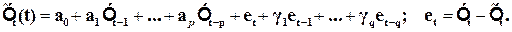(4.9)

1) Назначение: Если классическое уравнение регрессии (УР) оказалось неадекватным (например, имеет место смешенность остатков M[e_i]¹0, их автокорреляция, гетероскедантичность), то целесообразно построение разностной авторегрессионной модели.

2) Структура уравнения регрессии: В левой части уравнения регрессии стоит аппроксимируемая величина Z^(d) – разность порядка d, а в правой части линейная комбинация лаговых переменных порядка p, аппроксимирующая эту разность Z^(d):

(4.10)

Пример для разности первого порядка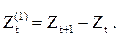

Для практического построения разности автореррессионной модели необходимо провести идентификацию модели, т.е. выбрать оптимальные с точки зрения адекватности и качество модели значения порядка разности d^* и порядка уравнения регрессии (числа лаговых переменных) р ^*.

Может быть использован следующий алгоритм:

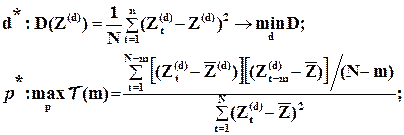(4.11)

Дата добавления: 2014-01-05