Проблема спецификации переменных. Мультиколлинеарность

Прогнозирование по разностной авторегрессионной модели.

Оценка коэффициентов регрессии.

В структуру разностной авторегрессии – регрессии оцениваемые коэффициенты модели 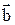входят линейным образом, поэтому применим классический метод наименьших квадратов:

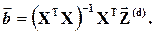(4.12)

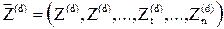- вектор наблюдений зависимой переменной.

Прогнозирование осуществляется как в обычном линейном уравнении регрессии. После получения точечного и интервального прогноза следует вернуться от разностей к зависимой переменной Y_t по формулам связи разностей с Y_t. Например, для разностей первого порядка получим соотношение:

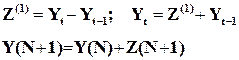(4.13)

Глава IV. Некоторые вопросы практического построения регрессионных моделей

Мультиколлениарность – это линейная взаимосвязь двух любых регрессоров X_j и X_k, (j, k = 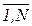), что является нарушением 7 предпосылки метода наименьших квадратов.

Здесь может быть два случая:

а) Два любых фактора имеют между собой линейную функциональную (детерминированную) связь

x_j =a+ bx _k; (5.1)

В этом случае соответствующий вектор столбцы базе данных x_ij, (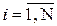) и x_{i k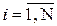}, () оказываются строго линейно – зависимыми и определитель матрицы нормальных уравнений равен нулю:

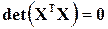(5.2)

Значит матрица 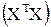необратима и оценить параметры уравнения регрессии по методу наименьших квадратов невозможно.

б) Линейная связь (5.1) стохастическая (скрытная). Однако она может быть выявлена путем вычисления коэффициента линейной парной корреляции 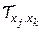если критерии Стьюдента 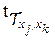значим, то стохастическая линейная взаимосвязь есть!

Следствия:

1). Матрица 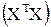нормальных уравнений формально обратима, но плохо обусловлена (её определитель 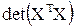очень мал, и тем меньше, чем сильнее взаимосвязь х_j и x_k). При большей размерности этой матрицы (десятки и сотни регрессоров) возникают вычислительные проблемы.

2) Если все же удалось построить уравнение регрессии с сохранением в нем мультиколлинеарных факторов, уравнение регрессии имеет плохое качество:

· Модель, как правило, неадекватна;

· Большие среднеквадратичные отклонения оцениваемых параметров ;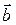

· Оценки неустойчивы по вариации исходных данных;

· Данные моделирования трудноинтерпретируемы;

Дата добавления: 2014-01-05