
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Двух шаговый метод наименьших квадратов
|
|
|
|
1. Исходные (неочищенные) регрессоры xj аппроксимируются методом линейных уравнений регрессии от выбранных инструментальных переменных {Zk},  .
.
 ()
()
Получаем m ЛУМР, причем, независимых друг от друга (метод наименьших квадратов применяется m - раз). Для этого используется классический метод наименьших квадратов. Здесь {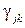 } - матрица искомых коэффициентов; j - номер строки этой матрицы, равный номеру исходного регрессора xj; k – номер члена в ЛУМР, равный номеру инструментальной переменной Zk. Классический метод наименьших квадратов используется поочередно для каждого xj.
} - матрица искомых коэффициентов; j - номер строки этой матрицы, равный номеру исходного регрессора xj; k – номер члена в ЛУМР, равный номеру инструментальной переменной Zk. Классический метод наименьших квадратов используется поочередно для каждого xj.
Замечание. В силу некоррелированности инструмент. переменная Zk с остатками E эти оценки получаются состоятельными метода наименьших квадратов.
 ()
()
 ()
()
N – число опытов; i – номер опыта;
Z – матрица планирования эксперимента, где базисные функции – линейные функции от Zk.

Замечание: переменные 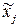 не коррелируют с ошибками регрессии
не коррелируют с ошибками регрессии 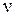 , поскольку они выражаются в виде линейной комбинации некоррелирующих с E переменных {Zk}.
, поскольку они выражаются в виде линейной комбинации некоррелирующих с E переменных {Zk}.
2. Будем рассматривать { 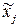 } как новые инструментальные переменные для Y и аппроксимируем Y через них.
} как новые инструментальные переменные для Y и аппроксимируем Y через них.
 ()
()
Вектор коэффициентов для каждой фиксированной компоненты 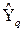 оцениваем снова с помощью классического метода наименьших квадратов:
оцениваем снова с помощью классического метода наименьших квадратов:

Всего получается таких l формул метода наименьших квадратов вида (); т.е.  ; где q - число исходных результативных переменных.
; где q - число исходных результативных переменных.
3. Поскольку все преобразования линейны, то подставляя () в () получим выражение оценки двухшагового метода наименьших квадратов через исходные (а значит экономически интерпретируемые) инструменты переменной Z j
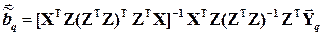 ()
()
Оценки [ bjq ]состоятельные
Замечание: Для нелинейного МУР применимость 2х – шаговой процедуры сохраняется, однако связь  с
с 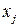 получается уже численная.
получается уже численная.
Вывод: Нужно сделать преобразования переменных перед применением 2х шагов метода наименьших квадратов
Пример: 
Вводим 

Далее 2х –шаговую процедуру можно применять по стандартной схеме к ()
Второй способ для систем одновременных уравнений (СОУ). Построить НСМ с числом нейронов в выходном слое, равном числу компонентов вектора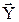
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 364; Нарушение авторских прав?; Мы поможем в написании вашей работы!