Критерий Больцано-Коши сходимости ряда

Рассмотрим ряд (А). Сходимость ряда по определению равносильна тому, что последовательность его частичных сумм 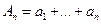сходится (т.е. имеет кон.предел).

Пусть последовательность частичных сумм 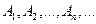сходится. Сходимость последовательности означает, что для 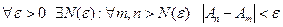(критерий Больцано-Коши для последовательности).

Пусть 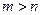. Тогда 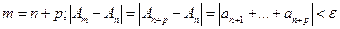, т.е. получим отрезок ряда меньше любого .

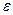Теорема (критерий Больцано-Коши). Для того, чтобы ряд (А) сходился необходимо и достаточно, чтобы для , т.е. чтобы достаточно далекие отрезки ряда становились по модулю как угодно малыми.

Пример:

Рассмотрим гармоничный ряд

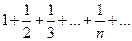
Средним гармонических чисел 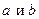называют такое числ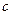о , что

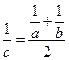
В выписанном ряде каждый член, начиная со второго, есть среднее гармоническое следующего и предыдущего членов ряда.

Исследуем данный ряд на сходимость с помощью критерия Больцано-Коши.

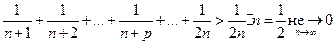, поэтому данный ряд расходится.

Дата добавления: 2014-01-05