Искажение линий и площадей в проекции Гаусса-Крюгера

Как известно, чтобы изобразить земную поверхность на плоскости для получения топографического плана, переходят от физической поверхности Земли к геометрической фигуре, в качестве которой принимают поверхность эллипсоида вращения сфероида (шара).

Поверхность сфероида изображается на плоскости с искажениями. Разработано много способов представления поверхности сфероида на плоскости, которые называются картографическими проекциями. В нашей стране принята равноугольная поперечно-цилиндрическая проекция Гаусса-Крюгера. При использовании данной проекции сохраняется подобие контуров на поверхности сфероида и на плане, но искажается длины сторон контуров и их площадей, т.е. масштаб изображений линий на плоскости в проекции Гаусса-Крюгера всегда крупнее того масштаба, который принят для составления плана. При этом укрупнение масштаба тем больше, чем дальше линия или участок расположены от осевого меридиана зоны.

Длина линии 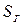на плане может быть вычислена по формуле

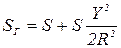(24)

где S – горизонтальное проложение линии местности; Y – ордината середины этой линии, т.е. расстояние от осевого меридиана зоны; R – средний радиус кривизны сфероида»6370км.

Из формулы (32) видно, что все линии на плане, больше соответствующих горизонтальных проложений линий местности на величину

.

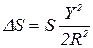Относительное искажение линии

зависит от удаления от осевого меридиана зоны и для края 6-тиградусной зоны в средних широтах РФ () составляет 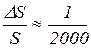. Если горизонтальное проложение линии местности равно 1000м, то она изобразиться на плане длиной 1000,5м.

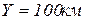
При , при 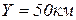, т.е. для линий расположенных на 100км и ближе от осевого меридиана зоны искажение можно не учитывать.

Искажение линий вызывает погрешности при определении площадей участков по плану. Исходя из подобия фигур в проекции Гаусса-Крюгера, запишем

,

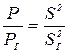отношение площади участка на местности относится к площади этого участка, определенного по плану как квадраты сходственных сторон.

Подставив в формулу величину 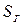, получим

.

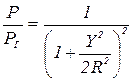Умножив числитель и знаменатель правой части на и пренебрегая малыми величинами порядка , получим

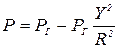(25)

Величина называется относительным искажением площади и в два раза больше относительного искажения линии. Из анализа формулы (31) следует, что для участков имеющих небольшую площадь поправку за искажение можно не учитывать, а для больших площадей ее следует учитывать только на краях шестиградусных зон.

Дата добавления: 2014-01-05