
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математическое описание динамики САР
|
|
|
|
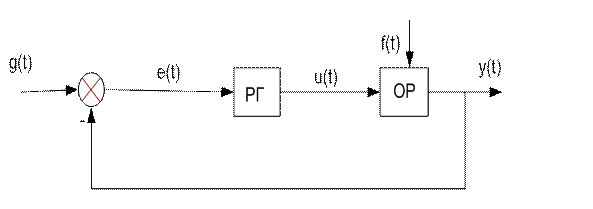
Рис. 1.7. Функциональная схема САР
На представленной схеме показано, что между входными и выходными сигналами существует непрерывная функциональная связь во времени. В данном случае САР будет характеризоваться следующими параметрами:
y(t) - управляемый параметр; u(t) - управляющее воздействие; f(t) - возмущающее воздействие; e(t) – рассогласование сигналов; g(t) - задающее воздействие. Значения этих параметров в моменты времени t1, t2,... tk дают полную информацию о состоянии САР. Пусть состояние ОР характеризуется функцией G(u,f,y), а регулятора - функцией Q(e,u), тогда закон функционирования системы может быть представлен в общем виде системой уравнений вида [1]:
| y (t) = G [ y(1), y(2),..., y(n), f, f(1),..., f(l), u, u(1),...,u(q)] | (1.1) |
| u (t) = Q [ e, e (1),... e (n), u(1),..., u(q)] | (1.2) |
| e (t) = g (t) - y (t) | (1.3) |
Переменные u и e - внутрение, математически их можно выразить через внешние переменные. Следовательно, можно записать:
| y = F [ y(1),...y(n), f, f(1),...f(l) , g, g(1),...g(m) ] | (1.4) |
Здесь под y(i), f(i), g(1) понимаются соответствующие производные. Уравнение (1.4) называется уравнением динамики. Оно описывает переходные процессы, происходящие в системе. При проектировании сложных технических систем возникают проблемы вычислительного плана особенно, если уравнения нелинейные или высокого порядка. В таких случаях при оценке процессов, описывающих поведение динамической системы, в первом приближении пользуются упрощенной математической моделью, которая получается в ходе линеаризации нелинейного уравнения. Рассмотрим эту процедуру.
Если F - аналитическая функция, то допускается разложение ее в ряд Тейлора в окрестности точки равновесия. В нашем случае точка равновесия есть точка, характеризующая установившееся состояние. Чем меньше отклонение от состояния равновесия, тем меньше ошибка, возникающая в результате замены нелинейного уравнения линейным. Допустим, что y(t) является функцией нелинейной, а F - аналитической. Учтем, что состояние равновесия характеризуется уравнением статики. Такое уравнение можно получить из уравнения (1.4), приравняв производные по времени к нулю:
| y0 = F (0,..., 0, f0, 0,...0, g0, 0,...,0). |
Пусть воздействия получили приращения и приняли вид:
| g = g0 + D g, f = f0 + D f. |
Тогда в системе возникает переходной процесс:
| y = y0 + D y. |
Представим функцию F рядом Тейлора в окрестности точки равновесия. Оставим в разложении только линейные члены, учитывая их весомость по сравнению с откидываемыми малыми величинами:
y = F (0,...,0,f0,0,...,0,g0,0,...,0) + 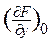  y + y + 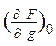  g + g + 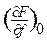  f +... f +...
|
Далее, учтем, что y0 = F (0,... 0, f0, 0,...0,g0, 0,...0) и отметим, что в уравнение динамики входят только отклонения, но не сами переменные, кроме того
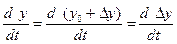 , поскольку , поскольку  = const. = const.
|
Поэтому символ приращения D можно опустить. Введем коэффициенты а , c
, c , b
, b равные частным производным функции F по g, f, y соответственно в точке равновесия. Перепишем уравнение динамики с учетом введенных переменных, получим:
равные частным производным функции F по g, f, y соответственно в точке равновесия. Перепишем уравнение динамики с учетом введенных переменных, получим:
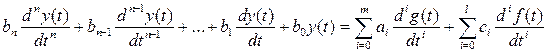
| (1.5) |
Уравнение (1.5) является линейным с постоянными коэффициентами. Оно называется уравнением динамики в первом приближении. По виду уравнения динамики различают модели, описываемые алгебраическими уравнениями, обыкновенными дифференциальными уравнениями, дифференциальными уравнениями в частных производных, уравнениями в конечных разностях. По виду коэффициентов уравнения различают модели с постоянными (детерминированными, стационарными) коэффициентами, с переменными (недетерминированными, нестационарными) параметрами, с квазистационарными параметрами, то есть стационарными в очень малых интервалах времени. По виду временных функций, различают модели непрерывные, дискретные (цифровые), дискретно-непрерывные. Стационарные и нестационарные системы могут быть как линейными, так и нелинейными. Нестационарные системы характерны тем, что при сдвиге входного возмущения во времени без изменения формы их выходные переменные не только сдвигаются во времени, но и меняют форму. Если входные сигналы в автоматических системах могут действовать непрерывно в течение всего времени работы системы, то такая система называется непрерывной. Любая система управления, поведение которой описывается линейными дифференциальными уравнениями с постоянными коэффициентами, является стационарной линейной системой. В заключение отметим, что системы управления по виду уравнений динамики разделяются на стационарные и нестационарные, линейные и нелинейные, многомерные и одномерные, непрерывные и дискретные.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 607; Нарушение авторских прав?; Мы поможем в написании вашей работы!