Типовые звенья обыкновенных линейных систем

Гармоническая функция

Гармонические функции на входе и выходе устройства могут быть

представленны следующим образом:

g_вх (t) =A_вх sin w t, g_вых (t) =A_вых sin (w t + Y).

Частотные характеристики A(w) и Y(w) описывают установившиеся вынужденные колебания, полученные при подаче на вход устройства гармонического воздействия. A(w) - амплитудно - частотная характеристика. Y(w) – фазо-частотная характеристика.

Обыкновенными называют линейные системы с постоянными параметрами. После многократного применения операции разбиения практически любую техническую систему в конечном итоге можно разбить на не подающиеся дальнейшему разбиению звенья четырех типов: умножающие, суммирующие, интегрирующие, дифференцирующие. Из названных типов звеньев к динамическим относятся интегрирующие и дифференцирующие. При разбиении (декомпозиции) схемы на элементарные звенья онсхема становится чрезмерно детальной, громоздкой и малонаглядной, поэтому в системах автоматического управления широкое применение находит разбиение схемы на типовые звенья несколько более сложной структуры, чем элементарные, но более соответствующие реальным элементам. Рассмотрим их.

Идеальное интегрирующее звено (интегратор)

Интегральное и дифференциальное уравнения звена имеют вид:

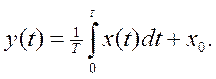
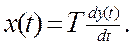
Здесь приняты следующие обозначения: х(t) – входной сигнал, у(t) – выходной сигнал. Воспользуемся изображением Лапласа, получим:

.

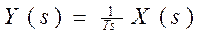Откуда нетрудно выразить передаточную функцию звена:

.

Переходная функция звена, то есть реакция звена на входное воздействие

х(t) = 1(t) при начальных условиях х(0) = 0, будет следующей:

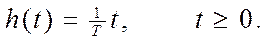
Она изображается прямой, наклоненной к оси t под углом arctg (1/T).

Импульсная переходная или весовая функция идеального интегрирующего звена является реакцией звена на типовое входное воздействие в виде импульсной дельта - функции х(t) = (t) и определяется выражением

При х(t) = (t) выходная величина y(t) скачком принимает постоянное значение, которое и сохраняет в дальнейшем. Примером приближенной реализации интегратора может служить двигатель постоянного тока, у которого постоянная времени мала в сравнении с временем переходного процесса системы, в которой двигатель работает.

Идеальное дифференцирующее звено

Дифференциальное уравнение звена имеет вид:

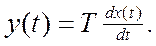
Воспользуемся преобразованием Лапласа и перепишем последнее уравнение:

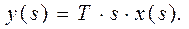
Передаточная функция определится выражением:

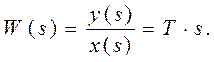
Переходная характеристика такого звена определяется выражением:

,

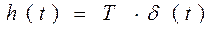где - импульсная дельта - функция. Переходная характеристика представляет собой импульс типа дельта - функции с площадью Т. Возможность представления реального звена идеальным дифференцирующим определяется соотношением постояной времени звена и дифференцируемого процесса. Чем больше инерция звена, тем с большей погрешностью оно будет дифференцировать быстро изменяющиеся функции. О близости реального звена к идеальному звену удобно судить по частотным характеристикам.

Отметим, что идеальный дифференциатор дает усиление гармонических колебаний, пропорционально частоте и опережение выходных колебаний по фазе 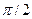независимо от частоты. Весьма близким к идеальному дифференцирующему звену является дифференцирующий усилитель с большим коэффициентом усиления. В той полосе частот, которая указана в паспорте усилителя, его передаточная функция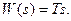

Выходная величина дифференцирующего звена при гармоническом воздействии пропорциональна частоте воздействия, и звено усиливает высокочастотные помехи, что сильно затрудняет его использование. Поэтому в моделирующих устройствах обычно стремятся обойтись без дифференцирующих звеньев. Это всегда возможно, если степень числителя передаточной функции моделирующего звена не выше степени знаменателя.

Неидеальное интегрирующее звено

Строго говоря, любое реальное интегрирующее звено неидеально.

Иногда грубое интегрирование выполняют с помощью статического звена, например, с помощью пассивной RC цепи, для которой ранее было найдено уравнение динамики 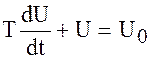. При переходе в s – область уравнение принимает вид или 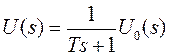. Передаточная функция такого звена определится выражением:

Дифференцирующее инерционное звено

Рассмотрим схему:

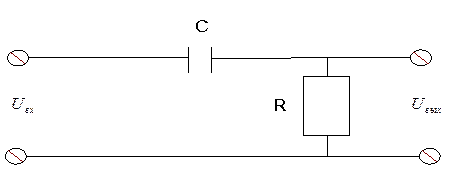
Рис. 1.10. Схема дифференцирующего звена с замедлением

Для этой схемы законы Кирхгофа для токов и напряжений имеют вид:

,

где у токов и напряжений опущен аргумент (время) с целью обеспечения наглядности математических выкладок. Далее учитывая, что

,

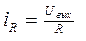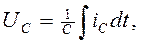
перепишем уравнение Кирхгофа для напряжений

,

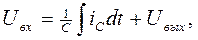Подставим последнее выражение 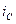в интеграл, получим

Продифференцируем левую и правую части уравнения, получим дифференциальное уравнение рассматриваемого звена:

Далее, чтобы получить выражение передаточной функции, умножим левую и правую части уравнения на одинаковый сомножитель Т = RС, применим преобразование Лапласа, перейдем к изображениям, сгруппируем члены нужным образом. Будем иметь

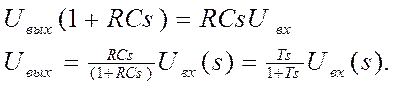
Погрешность замены идеального звена неидеальным звеном, можно уменьшить, выбрав T достаточно малым, и вводя большой коэффициент усиления k. Передаточная функция такого звена определится выражением:

.

Переходная функция звена, то есть реакция звена на входное воздействие

х(t) = 1(t) при начальных условиях х(0) = 0, будет следующей:

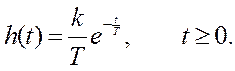
В момент включения h(0)=k, то есть выходная величина изменяется скачком аналогично изменению входной х(0) = 1.

Идеальное форсирующее звено

Введение производных в закон регулирования осуществляется обычно с помощью так называемых форсирующих звеньев. Идеальное форсирующее звено осуществляет сложение выходной величины с ее производной и имеет передаточную функцию

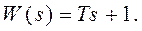
Апериодическое звено первого порядка

Рассмотрим звено с передаточной функцией

.

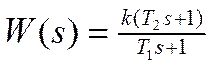В таком звене при 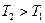преобладает форсирование (дифференцирование), при - инерционное запаздывание (интегрирование). Поэтому такое звено часто называют интегрирующим. При 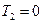, оно превращается в часто используемое звено, называемое статическим звеном первого порядка, инерционным, апериодическим. Величины k и T называются соответственно

коэффициентом усиления и постояной времени.

Апериодическое звено первого порядка имеетпередаточную функцию вида:

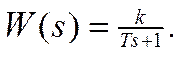
Как видно из формулы, свободный член полинома знаменателяравен 1. К такому стандартному виду можно привести передаточную функцию первого порядка, если разделить ее числитель и знаменатель на коэффициент отличный от 0 и 1.

Колебательное звено

Уравнение динамики такого звена было получено ранее на примере RLC контура. Такое звено имеет дифференциальное уравнение вида

.

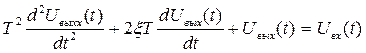Перейдем к изображению Лапласа, получим:

.

.

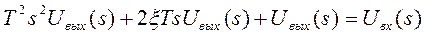Откуда следует выражение его передаточной функции

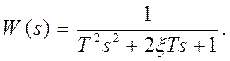
Колебательное звено, у которого 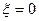, называется консервативным

(резонансным) звеном.

Аналогичным образом получены передаточные функции остальных типовых звеньев, результаты внесены в таблицу 1.1:

Таблица 1.1

Тип звена	Передаточная функция
1. Безынерционное звено	k, k = const
2. Идеальное дифференцирующее звено	k s
3.Дифференцирующее звено с замедлением	ks / (1+Ts)
4. Идеальное интегрирующее звено	k / s
5. Интегрирующее звено с замедлением	k / (s (1 + Ts))
6. Апериодическое звено 1-го порядка	k / (Ts+1)
7. Апериодическое звено 2-го порядка	k / (T2s^2+T1s+1)
8. Колебательное звено	k / (Ts^2+2xTs+1)
9. Идеальное форсирующее звено	Ts+1
10. Изодромное звено	k (Ts +1) / s
11. Консервативное звено	k / (T^2 s^2+ 1)

Дата добавления: 2014-01-05