Топология систем управления. Способы соединения элементов

Символическое изображение всех функциональных элементов и связей между ними, отражающее последовательность взаимодействия процессов в системе управления, называется функциональной или структурной схемой.

Если известна структурная схема и параметры системы, то можно, пользуясь аппаратом структурных преобразований, найти передаточную функцию любой системы.

При исследовании линейных систем важно уметь приводить структурные схемы к форме наиболее удобной для расчетов. Для этого необходимо научиться заменять одни структурные схемы на равноценые, но более удобные для проводимых расчетов или проводимого моделирования, что позволяет значительно упростить определение характеристик систем и сократить объем необходимых для этого вычислений. Всякая структурная схема представляет собой совокупность более простых структур, точек разветвления, сумматоров, соединенных между собой различными способами. Любое преобразование структурной схемы сводится к эквивалентной перестановке различных ее соседних элементов. Точки разветвления линейных систем называются узлами. Основной принцип перестановки элементов структурной схемы состоит в том, что все входные и все выходные переменные преобразуемого участка должны остаться неизменными. Одномерной системой управления называется система, имеющая один контур управления, то есть система с одной управляемой координатой и одним задающим воздействием. Многомерной САУ называется такая система управления, у которой несколько управляемых параметров. Рассмотрим способы соединения элементов в схеме и формулы передаточных функций типовых соединений.

Последовательное соединение

Рис. 1.11. Схема последовательного соединения звеньев

Передаточная функция последовательного соединения равна произведению передаточных функций входящих в соединение звеньев.

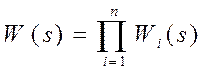
(1.9)

Параллельное соединение

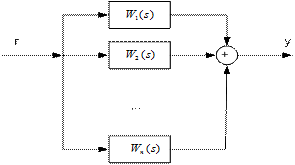
Рис. 1.12. Схема параллельного соединения звеньев

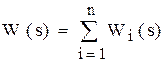
(1.10)

Передаточная функция параллельного соединения равна сумме передаточных функций входящих в соединение звеньев.

Соединение с обратной связью

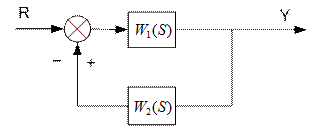
Рис. 1.13. Схема соединения звеньев с обратной связью

Передаточная функция обратного соединения равняется отношению передаточной функции звена в прямой цепи к произведению передаточных функций звеньев, стоящих в прямой и обратной цепи со знаком + для отрицательной обратной связи и со знаком - для положительной обратной связи, увеличенному на единицу:

.

(1.11)

Дата добавления: 2014-01-05