Логические основы ЭВМ, элементы и узлы

Организации и функционирования

В главе рассмотрены логические основы функционирования ЭВМ: основные положения алгебры логики и элементы логических схем, принципы построения компьютера (принципы фон Неймана). Показана история развития поколений ЭВМ, раскрыты различные типы архитектур ЭВМ, приводятся классификации ЭВМ по типу, по назначению, по уровню специализации, по типоразмерам, по типу используемого процессора. Подробно рассмотрен вопрос оценки производительности ЭВМ.

Ключевые слова: высказывание, логический элемент компьютера, конъюнкция, дизъюнкция, инверсия, эквиваленция, импликация, таблица истинности, триггер, регистр, сумматор, архитектура и структура компьютера, принципы фон Неймана, контроллер, магистрально-модульный принцип, магистраль, шина данных, шина адреса, шина управления, цифровые и аналоговые компьютеры, MIPS, MFLOPS.

С середины 60-х годов существенно изменился подход к созданию вычислительных машин. Вместо независимой разработки аппаратуры и некоторых средств математического обеспечения стала проектироваться система, состоящая из совокупности аппаратных (hardware) и программных (software) средств. При этом на первый план выдвинулась концепция их взаимодействия [104]. Так возникло принципиально новое понятие - архитектура ЭВМ. Однако, прежде чем перейти к детальному изучению архитектуры, вначале следует ознакомится с логическими основами функционирования ЭВМ: основными положениями алгебры логики и элементами логических схем.

При построении основных узлов ЭВМ (регистра, сумматора, шифратора и т.д.) используется алгебра логики [19]. Создателем алгебры логики по праву считают английского математика XIX века Дж. Буля, по имени которого логические функции получили название булевых функций. Основу математической логики составляет алгебра высказываний. Это освобождает матлогику от неопределенности в толковании логических выражений, показывающих связь между отдельными суждениями и понятиями.

Алгебра логики оперирует с высказываниями. Под высказыванием понимают повествовательное предложение, относительно которого можно утверждать, истинно оно или ложно. Например, выражение «Москва - столица России» истинно, а выражение «7 кг. < 300 гр.» - ложно. Высказывания принято обозначать заглавными буквами латинского алфавита: А, В, С,..., X, У и т.д. Если высказывание А истинно, то пишут А= true (A = 1 или A= t), а если оно ложно, то A = false (A=0 или А=f).

В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые высказывания. Истинность полученных высказываний зависит от истинности исходных высказываний и использованных для их преобразования логических операций. Для образования новых высказываний наиболее часто используются логические операции, выражаемые словами «не», «и», «или».

Логический элемент компьютера - это часть электронной схемы, которая реализует элементарную логическую функцию.

Логическими элементами компьютеров являются электронные схемы «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-НЕ» и другие (называемые обычно вентилями), а также триггер.

Может быть доказано, что с помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. На структурных схемах ЭВМ каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Работу логических элементов описывают с помощью таблиц истинности.

Логические операции. Рассмотрим логические операции и соответствующие им элементы логических схем.

Конъюнкция. Соединение двух (или нескольких) высказываний в одно с помощью союза «И» (AND) называется операцией логического умножения, или конъюнкцией. Эту операцию принято обозначать знаками «Ù», «&» или знаком умножения «х». Сложное высказывание А&В (AÙB) истинно только в том случае, когда истинны оба входящих в него высказывания. Истинность такого высказывания задается табл. 3.1. Таблица, описывающая связь между входными и выходными значениями функции, называется таблицей истинности.

Таблица 3.1

Таблица истинности конъюнкции

А	В	A&B
false	false	false
false	true	false
true	false	false
true	true	true

Логическая схема «И» реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных диаграммах схемы «И» с двумя входами представлено на рис. 3.1, а.

Единица на выходе схемы «И» будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.

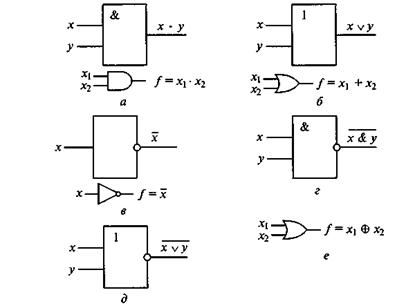
Рис. 3.1. Схемные логические элементы вычислительных машин

Связь между выходом z этой схемы и входами х и у описывается соотношением: z = x & у (читается как «х И у»). Операция конъюнкции на структурных схемах обозначается знаком «&».

Дизъюнкция. Объединение двух (или нескольких) высказываний с помощью союза «ИЛИ» (OR) называется операцией логического сложения, или дизъюнкцией. Эту операцию обозначают знаками «Ú» или знаком сложения «+». Сложное высказывание AÚВ истинно, если истинно хотя бы одно из входящих в него высказываний (табл. 3.2).

Таблица 3.2

Таблица истинности для логической суммы высказываний

А	В	AÚB	A XOR B
false	false	false	false
false	true	true	true
true	false	true	true
true	true	true	false

В последнем столбце табл. 3.2 размещены результаты модифицированной операции «ИЛИ» - «ИСКЛЮЧАЮЩЕЕ ИЛИ» (XOR - «сложению по модулю два»). Отличается от обычного «ИЛИ» последней строкой (см. также рис. 3.1, е).

Схема «ИЛИ» реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы «ИЛИ» будет единица, на ее выходе также будет единица.

Условное обозначение на структурных схемах схемы «ИЛИ» с двумя входами представлено на рис. 3.1, б. Связь между выходом z этой схемы и входами х и у описывается соотношением: z = x Ú у (читается как
«х ИЛИ у»).

Инверсия. Присоединение частицы «НЕ» (NOT) к некоторому высказыванию называется операцией отрицания (инверсии) и обозначается 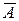(или ØА). Если высказывание А истинно, 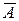то ложно, и наоборот (см. табл. 3.3).

Таблица 3.3

Таблица истинности отрицания

А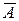
false	true
true	false

Схема «НЕ» (инвертор) реализует операцию отрицания. Связь между входом х этой схемы и выходом z можно записать соотношением 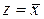, где 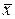читается как «НЕ х» или «ИНВЕРСИЯ х».

Если на входе схемы «0», то на выходе «1», и наоборот. Условное обозначение на структурных схемах инвертора - на рис. 3.1, в.

Вентили. Кроме схемных элементов, соответствующих перечисленным логическим операторам, в состав логических схем входят комбинированные связки, именуемые вентилями, например следующие.

Схема «И-НЕ» состоит из элемента «И» и инвертора - осуществляет отрицание результата схемы «И» (табл. 3.4). Связь между выходом Z и входами х и у схемы записывают как 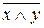, или «ИНВЕРСИЯ х И у». Условное обозначение на структурных схемах схемы «И-НЕ» с двумя входами представлено на рис. 3.1, г.

Таблица 3.4

Таблица истинности схемы «И-НЕ»

x	y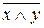
false	false	true
false	true	true
true	false	true
true	true	false

Схема «ИЛИ-НЕ» состоит из элемента «ИЛИ» и инвертора и осуществляет отрицание результата схемы «ИЛИ» (табл. 3.5). Связь между выходом z и входами х и у схемы записывают как 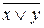, или
«ИНВЕРСИЯ х ИЛИ у». Условное обозначение на структурных схемах схемы «ИЛИ-НЕ» с двумя входами представлено на рис. 3.1, д.

Несколько слов о практической реализации схемных элементов в электронных цепях. Входные и выходные сигналы «1» представляются высоким уровнем напряжения на коллекторе транзистора (практически равным напряжению питания). Сигналу «0», наоборот, соответствует низкий уровень выходного напряжения.

Таблица 3.5

Таблица истинности схемы «ИЛИ-НЕ»

x	y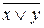
false	false	true
false	true	false
true	false	false
true	true	false

Следует отметить, что помимо операций «И», «ИЛИ», «НЕ» в алгебре высказываний существует ряд других операций. Например, операция эквиваленции (эквивалентности) А ~ В (или А º В, A EQV В) (табл. 3.6).

Таблица 3.6

Таблица истинности операции эквивалентности

А	В	A~B
false	false	true
false	true	false
true	false	false
true	true	true

Другим примером может служить логическая операция импликации или логического следования (А ®В, A IMP В), иначе говоря,
«ЕСЛИ А, то В» (табл. 3.7).

Таблица 3.7

Таблица истинности импликации

А	В	A®B
false	false	true
false	true	true
true	false	false
true	true	true

С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические выражения, которые также называются булевскими функциями. Например, С = ((Ā Ú В) → В) Ú А.

Чтобы избежать большого количества скобок в булевских функциях, принято следующее соглашение о старшинстве операций.

Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция слева направо.

Высказывания, образованные с помощью логических операций, называются сложными. Истинность сложных высказываний можно установить, используя таблицы истинности. Например, истинность сложного высказывания 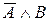определяется табл. 3.8.

Таблица 3.8

Таблица истинности высказывания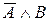

А	В		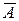В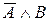
false	false	true	true	true
false	true	true	false	false
true	false	false	true	false
true	true	false	false	false

В алгебре высказываний можно проводить тождественные преобразования, заменяя одни высказывания равносильными им другими высказываниями[3]. Например, A®B равносильно 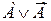, или А~В равносильно .

Элементы и узлы ЭВМ. Основойлюбого компьютера является ячейка памяти, которая может хранить данные или команды [29]. Основой любой ячейки памяти является функциональное устройство, которое может по команде принять или выдать один двоичный бит, а, главное, сохранять его сколь угодно долго. Такое устройство называется триггер, или защелка. Триггер - это устройство, имеющее два устойчивых состояния и способное скачком переходить из одного устойчивого состояния в другое при поступлении управляющих сигналов.

Триггер строится на основе базового набора логических схем
(рис. 3.2). Он собран на четырех логических элементах: два элемента «логическое НЕ» (схемы 1 и 2) и два элемента «логическое И-НЕ» (схемы 3 и 4). Триггер имеет два выхода Q и 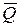. Сигнал на выходе Q соответствует значению, хранящемуся в триггере.

Выход 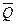используется при необходимости получить инверсное значение сигнала. Входы S и R предназначены для записи в триггер одного бита со значением ноль или единица.

Рассмотрим состояние триггера во время хранения бита. Пусть в триггер записан ноль (на выходе Q низкий уровень сигнала). Единица на выходе схемы 4 и единица на выходе схемы 1 поддерживают состояние выхода схемы 3 в состоянии нуля (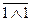=0). В свою очередь, ноль на выходе схемы 3 поддерживает единицу на выходе схемы 4 (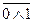=1). Такое состояние может поддерживаться триггером бесконечно долго.

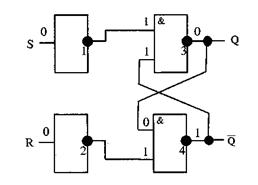
Рис. 3.2. Схема триггера в состоянии хранения бита информации

Для записи в триггер единицы подадим на вход S единицу. На выходе схемы 1 получится ноль, который обеспечит на выходе схемы 3 единицу. С выхода схемы 3 единица поступит на вход схемы 4, на выходе которой значение изменится на ноль (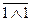=0). Этот ноль на входе схемы 3 будет поддерживать сигнал на ее выходе в состоянии единицы. Теперь можно снять единичный сигнал на входе S, на выходе схемы 3 все равно будет высокий уровень. Т.е. триггер сохраняет записанную в него единицу. Единичный сигнал на входе S необходимо удерживать некоторое время, пока на выходе схемы 4 не появится нулевой сигнал. Затем вновь на входе S устанавливается нулевой сигнал, но триггер поддерживает единичный сигнал на выходе Q, т.е. сохраняет записанную в него единицу.

Точно так же, подав единичный сигнал на вход R, можно записать в триггер ноль. Условное обозначение триггера показано на рис. 3.3.

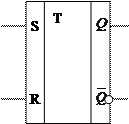Рис. 3.3. Условное обозначение триггера

Регистры. Триггер служит основой для построения функциональных узлов, способных хранить двоичные числа, осуществлять их синхронную параллельную передачу и запись, а также выполнять с ними некоторые специальные операции. Такие функциональные узлы называются регистрами.

Регистр представляет собой набор триггеров, число которых определяет разрядность регистра. Разрядность регистра кратна восьми битам: 8-, 16-, 32-, 64-разрядные регистры. Кроме этого в состав регистра входят схемы управления его работой. На рис. 3.4 приведена схема параллельного регистра хранения. Регистр содержит n триггеров, образующих n разрядов. Перед записью информации регистр обнуляется подачей единичного сигнала на вход «Сброс». Запись информации в регистр производится синхронно подачей единичного сигнала «Запись». Этот сигнал открывает входные вентили (схемы «логическое И»), и на тех входах X₁... X_n, где присутствует единичный сигнал, произойдет запись единицы. Чтение информации из регистра также производится синхронно, подачей сигнала «Чтение» на выходные вентили. Обычно регистры содержат дополнительные схемы, позволяющие организовать такие операции, как сдвиг информации - регистры сдвига (рис. 3.5) и подсчет поступающих единичных сигналов - регистры счетчики.

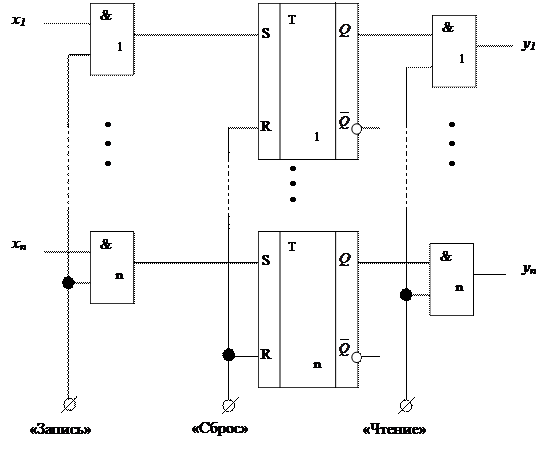Рис. 3.4. n-разрядный параллельный регистр хранения

с синхронной записью и чтением

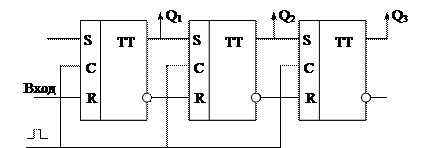
Рис. 3.5. 3-разрядный последовательный регистр

Сдвигающий регистр. Если на вход последовательного регистра (рис. 3.5), в который ранее было записано число, постоянно подавать ноль (записывать в него цифру 0), то с каждым тактом (импульсом на входе С) в него будет вводиться уровень нуля и хранившееся в нем число будет передвигаться по регистру, при этом крайняя от входа цифра будет из него выдвигаться.

Так как при этом происходит сдвиг хранившегося в регистре числа, то рассматриваемый регистр носит название сдвигающего. Сдвигающий регистр отличается от последовательного режимом работы и совпадает по схеме (рис. 3.5).

Работа сдвигающего вправо регистра, схема которого приведена на рис. 3.5 описывается таблицей 3.9. Цифры хранившегося в регистре числа выходят из него в той же последовательности, как и вводились. По окончании полного цикла работы сдвигающего регистра все ранее записанные в него цифры окажутся выведенными из регистра, и во всех его разрядах будут записаны нули.

Таблица 3.9

Цифра	Входы	Выходы
S	R	Q1	Q2	Q3
исходное состояние

Работа сдвигающего влево регистра, схема которого приведена на рис. 3.5 происходит аналогично. Разница лишь в направлении перемещения записанных ранее в регистр цифр табл. 3.10.

Таблица 3.10

	Выходы	Входы	Цифра
	Q1	Q2	Q3	S	R
				исходное состояние

При циклическом сдвиге выход триггера старшего разряда регистра соединяется со входом триггера младшего разряда, т.о. цифра, записанная в старшем разряде с каждым тактом записи перемещается в младший разряд, а цифра младшего разряда перемещается вправо в следующий разряд регистра.

Для обработки информации компьютер должен иметь устройство, выполняющее основные арифметические и логические операции над числовыми данными. Такие устройства называются а рифметико-логическими устройствами (АЛУ). В основе АЛУ лежит устройство, реализующее арифметическую операцию сложения двух целых чисел (сумматор). Остальные арифметические операции реализуются с помощью представления чисел в специальном дополнительном коде. Сумматор АЛУ представляет собой многоразрядное устройство, каждый разряд которого представляет собой схему на логических элементах, выполняющих суммирование двух одноразрядных двоичных чисел с учетом переноса из предыдущего младшего разряда. Результатом является сумма входных величин и перенос в следующий старший разряд. Такое функциональное устройство называется одноразрядным, полным сумматором. Его условное обозначение показано на рис. 3.6.

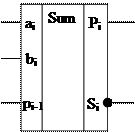Рис. 3.6. Условное обозначение полного одноразрядного сумматора

Многоразрядный сумматор состоит из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключен ко входу сумматора старшего разряда.

Рассмотренные выше функциональные элементы являются основными при построении схем компьютерных систем.

Дата добавления: 2014-01-05