Возможности и правила составления дифференциальных уравнений определяются знанием законов той области науки, с которой связана природа изучаемой задачи

Так, например,

· в механике могут использоваться законы Ньютона,

· в теории электрических цепей – законы Кирхгофа,

· в теории скоростей химической реакции – закон действия масс

· и так далее.

Распространены три основных способа математического описания систем:

- поэлементное описание системы;

- описание системы в переменных «вход - выход»;

- описание системы в переменных состояния (в нормальной форме Коши).

Поэлементное описание (чаще применяется инженерами) – при таком описании на основании изучения физических свойств объекта

- сначала получают уравнения для отдельных входящих в систему конструктивных или функциональных элементов;

- и для связей, объединяющих эти элементы в систему.

В левые части уравнений включают физические выходные переменные элементов и их производные по времени, в правые части - физические входные переменные – воздействия на элементы.

Некоторые переменные будут входными для одного элемента и выходными для другого.

Число переменных при таком описании оказывается большим, чем число управляемых переменных, так как оно включает «промежуточные» переменные, не всегда интересующие исследователя процесса управления в системе, хотя и важные для других специалистов, занятых конструированием элементов, их наладкой или обслуживанием.

К промежуточным переменным относятся, например, перемещения органов регуляторов, и.т.п., входные и выходные величины усилителей, преобразователей и т.д.

Например, имеется электрическая цепь

Поэлементное описание

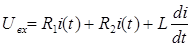
- промежуточная переменная

Описание системы в переменных «вход- выход» (модели вход – выход).

Для получения описания системы в целом исследователь исключает все не интересующие его промежуточные переменные и в уравнениях остаются только регулируемые величины (и их производные), записываемые в левых частях уравнений, и возмущающие и управляющие воздействия на систему в правых частях.

Выразив промежуточную переменную из второго уравнения и подставив в первое уравнение, получим дифференциальное уравнение электрической цепи для приведенного ранее примера в переменных «вход – выход»:

Модель системы в переменных «вход-выход» представляет собой дифференциальное уравнение n -го порядка.

В приведенных видах описания число входящих в уравнения физических переменных, как правило, оказывается недостаточным для полного описания состояния динамической системы, в том смысле, что по их набору в один момент времени еще нельзя определить их значения во все последующие моменты.

Разумеется, из этого не следует, что уравнения непригодны для исследования, просто, кроме самих переменных, в фиксированный начальный момент времени надо задавать еще некоторые из их производных.

Дата добавления: 2014-01-05